最近我们被客户要求撰写关于检测异常值的研究报告。这个例子展示了如何使用分位数随机林来检测异常值。
分位数随机林可以检测到与给定X的Y的条件分布有关的异常值。
可下载资源
离群值是一些观测值，它的位置离数据集中的大多数其他观测值足够远，可以认为是异常的。离群观测的原因包括固有的变异性或测量误差。异常值显著影响估计和推断，因此检测它们决定是删除还是稳健分析非常重要。
分位数回归森林(Quantile Regression Forests)，一般回归模型预测均值，但该算法预测数据的分布。它可以用来预测给定输入的价格分布，例如，给定一些属性，汽车价格分布的第25和75百分位是多少。
大多数预测器在预测期间返回E(Y|X)，这可以解释为这个问题的答案，给定输入，输出的期望值是多少?
分位数方法，在q处返回y，其中F(Y =y|X)=q，其中q是百分位数，y是分位数。一个有用的快速用例是当有许多异常值影响条件平均值时。有时重要的是获得不同百分比的估计值(例如，在对曲线进行评分时)。
注意:一些机器学习模型还返回P(Y|X)的整个分布。比如高斯过程和蒙德里安森林。一个有用的应用是超参数优化，其中条件分布P(Y|X)是平衡开发和探索的必要条件。
分位数决策树
扩展标准决策树以提供百分位数的预测是相当简单的。当一个决策树是合适的，诀窍是不仅要在叶节点上存储目标的充分统计量，如均值和方差，而且要在叶节点上存储所有的目标值。在预测中，这些被用来计算经验分位数估计。
假设参数min_samples_leaf被设置为5，那么对于一个新的样本X，当确定Y|X在不同量子位上时，叶中的5个样本被赋予相同的权重。如果min_samples_leaf被设置为1，那么期望就等于每百分位上的分位数。
注:分位数的经验估计有很多方法。scikit-garden，依赖于这个加权百分位数方法
分位数回归森林
同样的方法可以扩展到随机森林。为了估计F(Y= y |x)=q, y_train中的每个目标值都有一个权值。
非正式地说，这意味着对于一个新的未知样本，我们首先找到它落在每棵树上的叶子。然后，对于训练数据中的每一个(X, y)，在每棵树上按如下方式赋予y一个权重。
-
如果它和新样本在同一片叶子上，那么重量就是样本在同一片叶子上的比例。
-
如果没有，则权重为零。
每个y的权值在所有树中求和并取平均值。既然我们有一个目标值数组和一个与这些目标值对应的权重数组，我们可以用它来测量经验分位数估计值。
为了演示异常值检测，此示例：
从具有异方差性的非线性模型生成数据，并模拟一些异常值。
生长回归树的分位数随机森林。
估计预测变量范围内的条件四分位（Q1、Q2和Q3）和_四分位_距（IQR）。
将观测值与边界进行比较，边界为F1=Q1−1.5IQR和F2=Q3+1.5IQR。任何小于F1或大于F2的观测值都是异常值。
生成数据
从模型中生成500个观测值
在0 ~ 4π之间均匀分布，εt约为N(0,t+0.01)。将数据存储在表中。
rng('default'); % 为保证重复性
randsample(linspace(0,4*pi,1e6),n,true)';
epsilon = randn(n,1).*sqrt((t+0.01)); 将五个观测值沿随机垂直方向移动90%的值。
numOut = 5;
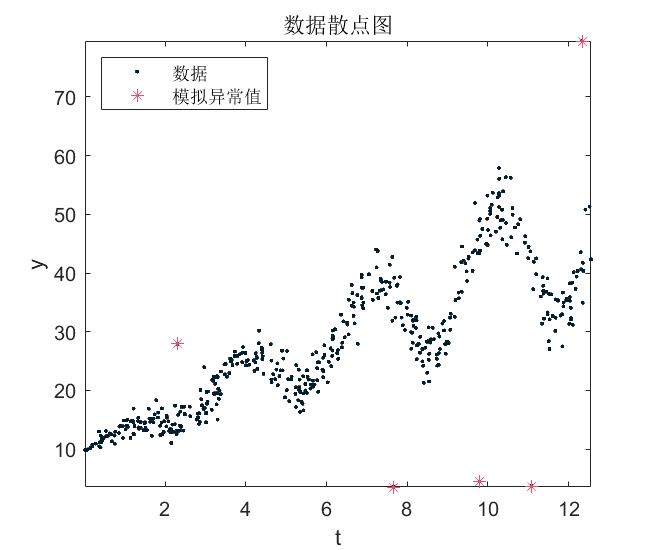
Tbl.y(idx) + randsample([-1 1],numOut,true)'.*(0.9*Tbl.y(idx)); 绘制数据的散点图并识别异常值。
plot(Tbl.t,Tbl.y,'.');
plot(Tbl.t(idx),Tbl.y(idx),'*');
title('数据散点图');
legend('数据','模拟异常值','Location','NorthWest');
生成200棵回归树。
Tree(200,'y','regression');返回是一个TreeBagger集合。
预测条件四分位数和四分位数区间
使用分位数回归，估计t范围内50个等距值的条件四分位数。
linspace(0,4*pi,50)';
quantile(pred,'Quantile');
quartile是一个500 × 3的条件四分位数矩阵。行对应于t中的观测值，列对应于概率。
在数据的散点图上，绘制条件均值和中值因变量。`
plot(pred,[quartiles(:,2) meanY]);
legend('数据','模拟的离群值','中位数因变量','平均因变量',... 随时关注您喜欢的主题
虽然条件均值和中位数曲线很接近，但模拟的离群值会影响均值曲线。
计算条件IQR、F1和F2。
iqr = quartiles(:,3) - quartiles(:,1);
f1 = quartiles(:,1) - k*iqr;
k=1.5意味着所有小于f1或大于f2的观测值都被认为是离群值，但这一阈值并不能与极端离群值相区分。k为3时，可确定极端离群值。
将观测结果与边界进行比较
绘制观察图和边界。
plot(Tbl.t,Tbl.y,'.');
legend('数据','模拟的离群值','F_1','F_2');
title('使用分位数回归的离群值检测') 所有模拟的异常值都在[F1，F2]之外，一些观测值也在这个区间之外。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
Python个人收入影响因素模型构建：回归、决策树、梯度提升、岭回归
