“聚类是将数据集分为几组的过程，其中包括相似的数据点”。聚类是一种无监督的机器学习，在您拥有未标记的数据时使用。
比如坐在餐馆的用餐者。假设餐厅中有两个桌子。桌子1中的人可能彼此相关，可能是一组家庭成员或同事。
类似的，桌子2中的人可能彼此相关。但是，当比较坐在两个桌子的人时，他们是完全不同的，可能根本没有关联。
可下载资源
聚类也以相同的方式工作。一个聚类中的数据点与另一聚类中的数据点完全不同。同一聚类中的所有点都相同或彼此相关。
聚类具有不同的算法。最受欢迎的是K-均值聚类。
什么是K均值聚类？
K-Means是一种聚类算法，其主要目标是将相似的元素或数据点分组为一个聚类。 K-均值中的“ K”代表簇数。
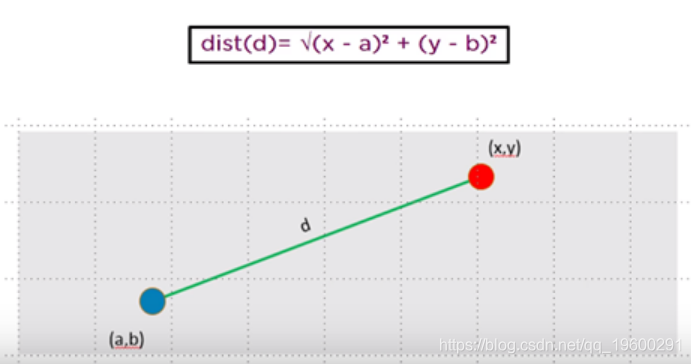
距离量度将确定两个元素之间的相似性，并将影响簇的形状。通常，欧几里得距离将用于K-Means聚类
欧几里得距离是“普通”直线。它是欧氏空间中两点之间的距离。
K-Means算法如何工作？
输入：样本集D，簇的数目k，最大迭代次数N；
输出：簇划分（k个簇，使平方误差最小）；
算法步骤：
（1）为每个聚类选择一个初始聚类中心；
（2）将样本集按照最小距离原则分配到最邻近聚类；
（3）使用每个聚类的样本均值更新聚类中心；
（4）重复步骤（2）、（3），直到聚类中心不再发生变化；
（5）输出最终的聚类中心和k个簇划分；
SAS中的K-均值聚类
让我们来看一个著名的IRIS数据集。使用proc检查数据集
/* 检查数据内容 */
proc means data=work.iris N Nmiss mean median max min;
run;它具有150个观测值和5个变量。未检测到缺失值或离群值。我们将仅使用四个变量，即sepal_length，sepal_width，petal_length和petal_width。数据集以“ cm”为单位。可以删除“目标”变量，因为它是类别变量。
关于鸢尾花数据集的简短介绍。这是一个多变量数据集，由英国统计学家 、 生物学家 罗纳德·费舍尔（Ronald Fisher） 在1936年为他的研究论文引入 。
在分析数据集之前了解数据。
/* 删除目标列将新数据保存为IRIS1 */
drop target;
run;在运行聚类分析之前，我们需要将所有分析变量（实数变量）标准化为均值零和标准偏差为1（转换为z分数）。在这里，我们的数据集已经标准化。
/* 聚类分析 */
method = centroid ccc print=15 outtree=Tree;METHOD => 确定过程使用的聚类方法。在这里，我们使用CENTROID方法。
CCC 是聚类标准—它有助于找出最佳的聚类点。
需要找出最佳聚类簇。
前三个特征值约占总方差的99.48％，因此，建议使用三个聚类。但是，可以在ccc图中对其进行交叉验证。
从图中看到，聚类标准有15个值（如我们在代码输出中给出的= 15）
从上面的CCC图可以看出，肘部下降在3个聚类。因此，最佳群集将为3。
为了将150个观测值中的每个观测值分类为三个聚类，我们可以使用proc树。ncl = 3（我们的最佳簇为3）。
/* 保留 3个聚类 */
proc tree noprint ncl=3 out= 
150个观察结果分为三类。
使用proc candisc和proc sgplot创建散点图
/*生成散点图 */
proc sgplot data = can;
title " 
我们可以看到，分析清楚地将三个聚类簇分开。聚类簇1为蓝色， 2为红色， 3为绿色。
K-均值聚类的优缺点
优点：
1）即使违背有些假设，也能很好地工作。
2）简单，易于实现。
3）易于解释聚类结果。
4）在计算成本方面快速高效。
缺点：
1）即使输入数据具有不同的簇大小，均匀效果使得结果经常会产生大小相对一致的簇。
2）不同密度的数据可能不适用于聚类。
3）对异常值敏感。
4）在K均值聚类之前需要知道K值。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频讲解】Python深度神经网络DNNs-K-Means（K-均值）聚类方法在MNIST等数据可视化对比分析
Python量子计算聚类Q-means（量子k-means）算法分析电路数据实现可视化
TensorFlow深度学习框架改进K-means聚类、SOM自组织映射神经网络算法及上海招生政策影响分析研究
Python回归、聚类、相关分析上海公租房租金满意度影响因素数据可视化
