R2WinBUGS软件包提供了从R调用WinBUGS的便捷功能。

由Kaizong Ye，Liao Bao撰写

它自动以WinBUGS可读的格式写入数据和脚本，以进行批处理（自1.4版开始）。WinBUGS流程完成后，可以通过程序包本身将结果数据读取到R中（这提供了推断和收敛诊断的紧凑图形摘要），也可以使用coda程序包的功能对输出进行进一步分析。

WinBUGS软件可从http://www.mrc-bsu.cam.ac.uk/bugs/ 免费获得。

R是一种“用于数据分析和图形处理的语言”，是一种实现该语言的开放源代码和免费提供的统计软件包，请参见http://www.R-project.org/。 R和R2WinBUGS可从CRAN 获得，即http://CRAN.R-Project.org或其镜像之一。

贝叶斯层级模型（Bayesian Hierarchical Model）是统计分析中一种有效的分析方法，尤其是当变量有很多而且相互之间有说不清道不明的关系的时候。

线性回归模型

要想理解贝叶斯层级模型就想要理解贝叶斯回归模型。废话不多说，直接上表达式。

来个熟悉的线性回归模型： $Y=X \bm{\beta}+\epsilon, \quad \epsilon \sim N(0,\sigma^2)；$

$Y=(y_1,\cdots,y_n)^T, \quad \epsilon=(\epsilon_1,\cdots,\epsilon_n)^T, X=\begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1j}\\ 1 & x_{21} & x_{22} & \cdots & x_{2j}\\ \vdots & \vdots & \vdots & \vdots & \\ 1 & x_{n1} & x_{n2} & \cdots & x_{nj} \end{bmatrix}。$

拆开来就是 $Y=\beta_0 + \sum_{j=1}^p\beta_j\mathbf{x}_j+\epsilon=\beta_0+\beta_1\mathbf{x}_1+\beta_2\mathbf{x}_2+\cdots+\beta_p\mathbf{x}_p+\epsilon$ 。

然后就是用最小二乘法（Ordinary Least Square）。

$\hat{\bm{\beta}} = \arg\min_{\beta}\parallel Y-X\bm{\beta}\parallel ^2= \min \sum_{i=1}^n (y_i-\sum_{j=1}^px_{ij}\beta_j)^2$

$\Rightarrow \hat{\bm{\beta}}= (X^TX)^{-1}X^TY$ 。

如果从概率分布的角度来说就需要用极大似然估计（Maximum Likelihood Estimation）。

首先需要构造似然函数。对于一个普通的线性回归模型来说， $Y$ 是由 $\beta$ 、 $X$ 和 $\sigma$ 决定的，其中 $X$ 是已知的。所以我们需要估计的是参数 $\beta$ 和 $\sigma$ 。

通过构造似然函数，并通过对参数求偏导来使似然函数取到最大值，从而得到参数的无偏估计。具体怎么操作网上很多，我就不写了（懒得打公式，哈哈哈）。

得出的结果和最小二乘求出来的是一样的。同时可以证明残差方差 $\sigma^2$ 的无偏估计 $\hat{\sigma}^2$ 就是 $Y$ 的方差。

贝叶斯回归

贝叶斯统计与频率统计最大的区别在于贝叶斯学派认为所有我们看到的概率事件都是基于先验概率。也就是说，所有的（超）参数都是服从其自身的先验分布！拿线性回归的例子来说， $\beta$ 和 $\sigma^2$ 是概率分布，并且是来自它们的联合先验（joint prior）分布，不是值，是分布！

$\beta,\sigma^2 \sim p(\beta,\sigma^2)$

我们的目的是估计 $\beta$ 和 $\sigma^2$ 的后验分布，因此我们需要贝叶斯公式： $P(\beta,\sigma^2|Y)=\frac{P(Y|\beta,\sigma^2)P(\beta,\sigma^2)}{P(Y)} \propto P(Y|\beta,\sigma^2)P(\beta,\sigma^2)$ 。因为 $\beta$ 和 $\sigma^2$ 相互独立，所以 $P(\beta,\sigma^2|Y)=P(\beta|Y,\sigma^2)P(\sigma^2|Y,\beta) \propto P(Y|\beta,\sigma^2)P(\beta)P(\sigma^2)$ 。

这里 $\beta$ 的先验 $P(\beta)$ 和 $\sigma^2$ 的先验 $P(\sigma^2)$ 是可以自己随意决定。

一般来说， $\beta \sim N(\mu_{\beta},\sigma^2_{\beta})$ 。

关于 $\sigma$ 有两种常用的先验，一种是 $\sigma \sim \operatorname{Uniform}(0,a)$ ；另一种是令 $\frac{1}{\sigma^2}=\tau$ ， $\tau \sim \Gamma(a,b)$ 。

从而我们就可以求得 $\beta$ 的后验分布 $P(\hat{\beta}|Y,\sigma^2)$ 和 $\sigma^2$ 的后验分布 $P(\hat{\sigma}^2|Y,\beta)$ 。

总结一下就是这个样子的：

$\begin{aligned} y_{i} \mid \mu_{i}, \sigma^{2}, \mathbf{x}_{i} & \sim N\left(\mu_{i}, \sigma^{2}\right), \quad \mathbf{i}=1, \ldots, \mathrm{n} \\ \mu_{i} &=\mathbf{x}_{i}^{T} \boldsymbol{\beta} \\ \beta_{j} & \sim N\left(\mu_{\beta_j}, \sigma_{\beta_{j}}^{2}\right), \quad \mathrm{j}=0, \ldots, \mathrm{p} \\ \sigma^{-2}=\tau & \sim \Gamma\left(a, b\right)\end{aligned}$

$\mu_{\beta_j}, \sigma_{\beta},a,b$ 的值都是自己定的，作为已知数据。

至于如何去求后验分布，基本上都是用的是蒙托卡罗-马尔可夫方法（MCMC），具体有可以分成M-H (Metropolis-Hastings)抽样算法和Gibbs抽样算法。当然也有用变分贝叶斯算法的。很多帖子都有做这类的介绍，这里不做过多陈述。

贝叶斯层级模型

介绍完贝叶斯回归模型，接下来就来说说贝叶斯层级模型。所谓层级就是将原本的参数作为变量继续进行估计。继续拿上面的线性回归举例。咱们刚刚讨论了贝叶斯线性模型的目标是通过 $\beta$ 和 $\sigma^2$ 的先验分布来估计 $\beta$ 和 $\sigma^2$ 的后验分布。现在经过研究，我们发现 $\beta$ 和 $\sigma^2$ 的先验分布会受其他因素的影响，我们需要通过额外数据来估计 $\beta$ 和 $\sigma^2$ 的先验，而不能自己随意决定！

这里任然是用 $\beta \sim N(\mu_{\beta},\sigma^2_{\beta})$ ， $\sigma^{-2} \sim \Gamma(a,b)$ 举例。其中每一个参数 $\mu_{\beta_j},\sigma^2_{\beta},a,b$ 都可能有各自的先验分布。整合起来就是

$\begin{aligned} \text{level 1}\\ y_{i} \mid \mu_{i}, \sigma^{2}, \mathbf{x}_{i} & \sim N\left(\mu_{i}, \sigma^{2}\right), \quad i=1, \ldots, \mathrm{n} \\ \mu_{i} &=\beta_0+\sum_{j=1}^{p} x_{ij} \beta_j, \\ \beta_{j} & \sim N\left(\mu_{\beta_j}, \sigma_{\beta}^{2}\right), \quad j=0, \dots, \mathrm{p}, \\ \sigma^{-2}=\tau & \sim \Gamma\left(a, b\right);\\ \hline \text{level 2}\\ \mu_{\beta_j}&=\gamma_0+\sum_{k=1}^{q}w_{jk} \gamma_k ,\\ \gamma_k &\sim N\left(\mu_{\gamma_k},\sigma^2_{\gamma}\right), \quad k=0, \dots,q\\ \sigma^{-2}_{\beta}=\tau_{\beta} & \sim \Gamma\left(a_{\beta}, b_{\beta}\right), \\ a & \sim \operatorname{Uniform}\left(a_1, a_2\right), \\ b & \sim \operatorname{Uniform}\left(b_1, b_2\right). \end{aligned}$

这是一个完整的两层贝叶斯回归模型。有些时候，例如 $\sigma_\beta^2$ 就是已知的，那么这里就不需要再假设它有先验了。这种时候这个模型的层就是一层半。

如果继续衍生下去，让已知的参数继续变为未知，那么就会出来三层、四层、五层……贝叶斯层级模型。

提前说一下，我是用R语言来做分析的，但贝叶斯层级模型是调用了jags来跑的。R里面有一个rjags的包，同时也要下载jags程序，Just Another Gibbs Sampler。

如果可以使用Internet连接，则可以在R命令提示符下键入

install.packages(
"R2WinBUGS")

来安装R2WinBUGS。别忘了用

library(R2WinBUGS)

例子

学校数据

学术能力测验（SAT）衡量高中生的能力，来帮助大学做出入学决定。我们的数据来自1970年代后期进行的一项实验，来自八所高中的SAT-V（学业能力测试语言）。SAT-V是由教育测试服务局管理的标准多项选择测试。该服务对所选学校中每所学校的教练计划的效果很感兴趣。

可下载资源

完整程序、数据和文档（word）

最受欢迎的见解

1.matlab使用贝叶斯优化的深度学习

2.matlab贝叶斯隐马尔可夫hmm模型实现

3.R语言Gibbs抽样的贝叶斯简单线性回归仿真

4.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

5.R语言中的Stan概率编程MCMC采样的贝叶斯模型

6.Python用PyMC3实现贝叶斯线性回归模型

7.R语言使用贝叶斯层次模型进行空间数据分析

8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

9.matlab贝叶斯隐马尔可夫hmm模型实现

实现

R2WinBUGS软件包的实现非常简单。 main“函数bugs（）由用户调用。原则上，它是对其中逐步调用的其他几个函数的包，如下：

bugs.data.inits（）写入数据文件’ data.txt”和“ inits1.txt”，“ inits2.txt” …进入工作目录。
bugs.script（）写入WinBUGS用于批处理的文件“ script.txt”。
bugs.run（）更新WinBUGS注册表，调用WinBUGS，并使用 ‘script.txt’ 以批处理模式运行它。
bugs.sims（）如果参数codaPkg已设置为false（默认值）才调用。
否则，bugs（）返回存储数据的文件名。例如，这些可以通过打包的coda 导入，该软件包提供了收敛诊断，蒙特卡洛估计的计算，迹线图等功能。
bugs.sims（）函数将WinBUGS中的模拟读取到R中，将其格式化，监视收敛，执行收敛检查并计算中位数和分位数。它还为bugs（）本身准备输出。
这些功能不由用户直接调用。参数将从bugs（）传递给其他函数。

自适应网页宽度的 Youku 视频

视频

R语言中RStan贝叶斯层次模型分析示例

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

例子

我们将 R2WinBUGS提供的功能应用于示例数据并分析输出。

学校数据

示例数据：

> schools

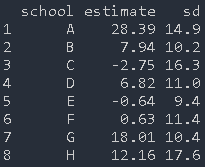
为了对这些数据进行建模，我们使用了Gelman等人提出的层次模型。我们假设每所学校的观测估计值具有正态分布，且均值theta 和方差tau.y，逆方差为1 =σ.y2，其先验分布在（0,1000）上是均匀的。对于均值theta，我们采用另一个正态分布平均为mu.theta和逆方差为tau.theta。有关其先验分布，请参见以下WinBUGS代码：

model {
for (j in 1:J)
{
y[j] ~ dnorm (theta[j], tau.y[j])
theta[j] ~ dnorm (mu.theta, tau.theta)
tau.y[j] <- pow(sigma.y[j], -2)
}
mu.theta ~ dnorm (0.0, 1.0E-6)
tau.theta <- pow(sigma.theta, -2)
sigma.theta ~ dunif (0, 1000)
}

此模型必须存储在单独的文件中，例如’schools.bug’2，在适当的目录中，例如c：/ schools /。在R中，用户必须准备bugs（）函数所需的数据输入。这可以是包含每个数据向量名称的列表，例如

WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

阅读文章 ➜

> J <- nrow(schools)

使用这些数据和模型文件，我们可以运行MCMC模拟以获取theta， mu.theta和sigma.theta的估计值。在运行之前，用户必须确定要运行多少个链（n.chain = 3）和迭代次数（n.iter = 1000）。另外，用户必须指定链的初始值，例如通过编写函数：

> inits <- function(){
+ list(theta = rnorm(J, 0, 100), mu.theta = rnorm(1, 0, 100),
+ sigma.theta = runif(1, 0, 100))
+ }

可以开始MCMC模拟，R中的参数bugs.directory必须指向WinBUGS的安装目录。可以通过print（schools.sim）方便地输出school.sim对象中的结果。

随时关注您喜欢的主题

对于此示例，将获得类似的结果

Inference for Bugs model at "c:/schools/schools.bug"
3 chains, each with 1000 iterations (first 500 discarded)
n.sims = 1500 iterations saved
mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff
theta[1] 11.1 9.1 -3.0 5.0 10.0 16.0 31.8 1.1 39
theta[2] 7.6 6.6 -4.7 3.3 7.8 11.6 21.1 1.1 42
theta[3] 5.7 8.4 -12.5 0.6 6.1 10.8 21.8 1.0 150
theta[4] 7.1 7.0 -6.6 2.7 7.2 11.5 21.0 1.1 42
theta[5] 5.1 6.8 -9.5 0.7 5.2 9.7 18.1 1.0 83
theta[6] 5.7 7.3 -9.7 1.0 6.2 10.2 20.0 1.0 56
theta[7] 10.4 7.3 -2.1 5.3 9.8 15.3 25.5 1.1 27
theta[8] 8.3 8.4 -6.6 2.8 8.1 12.7 26.2 1.0 64
mu.theta 7.6 5.9 -3.0 3.7 8.0 11.0 19.5 1.1 35
sigma.theta 6.7 5.6 0.3 2.8 5.1 9.2 21.2 1.1 46
deviance 60.8 2.5 57.0 59.1 60.2 62.1 66.6 1.0 170
pD = 3 and DIC = 63.8 (using the rule, pD = var(deviance)/2)
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC is an estimate of expected predictive error (lower deviance is better).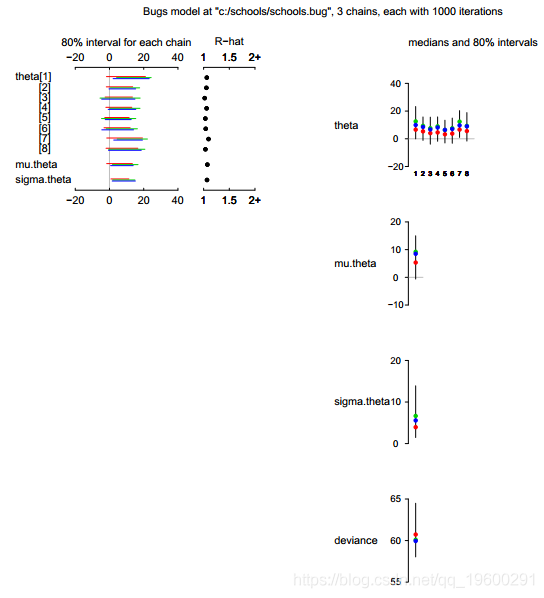

此外，用户可以通过输入plot（schools.sim）生成结果图。

结果图如图所示。在该图中，左列显示了以下内容的快速摘要：
推论和收敛（所有参数的Rb都接近1.0，表明三个链的良好混合，因此近似收敛）；右列显示每组参数的推论。从右栏中可以看到，R2WinBUGS使用 WinBUGS中的参数名称将输出构造为标量，向量和参数数组。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言用WinBUGS 软件对学术能力测验（SAT）建立层次（分层）模型

R2WinBUGS软件包提供了从R调用WinBUGS的便捷功能。

线性回归模型

贝叶斯回归

贝叶斯层级模型

例子

学校数据

实现

例子

WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

随时关注您喜欢的主题

此外，用户可以通过输入plot（schools.sim）生成结果图。

相关文章

R语言用WinBUGS 软件对学术能力测验（SAT）建立层次（分层）模型

R2WinBUGS软件包提供了从R调用WinBUGS的便捷功能。

线性回归模型

贝叶斯回归

贝叶斯层级模型

例子

学校数据

实现

例子

WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

随时关注您喜欢的主题

此外，用户可以通过输入plot（schools.sim）生成结果图。

相关文章

关注有关新文章的微信公众号