
我们添加了一个粗略而有效的约束,以防止导致“ NA”值的参数值:目标函数返回较大的正值。
在本项目中,我们被客户要求研究如何将Nelson-Siegel-Svensson(NSS)模型拟合到数据。由于我们将使用随机技术进行优化,因此我们应该重新运行几次。变量nRuns设置示例重启的次数。
可下载资源
将NS模型拟合到给定的零利率
NS模型
我们使用给定的参数betaTRUE创建“真实”的收益曲线yM。付款时间(以年为单位)在向量tm中。
> tm <- c(c(1, 3, 6, 9)/12, 1:10)
> betaTRUE <- c(6, 3, 8, 1)
> yM <- NS(betaTRUE, tm)
> par(ps = 11, bty = "n", las = 1, tck = 0.01, mgp = c(3, 0.2, 0), mar = c(4, 4, 1, 1))
> plot(tm, yM, xlab = "maturities in years", ylab = "yields in %")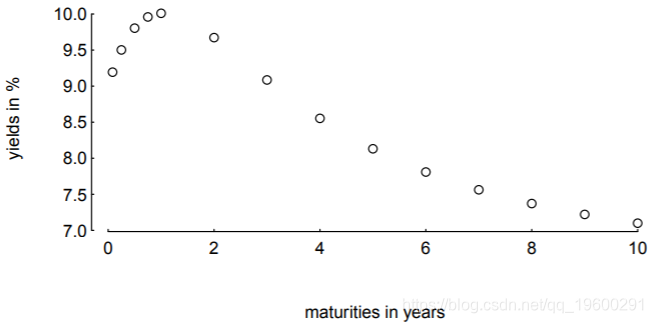
目的是通过这些点拟合平滑曲线。我们从目标函数OF开始。它有两个参数:param和list数据(包含所有其他变量)。返回观察到的(“市场”)收益率yM的向量与参数param的模型收益率之间的最大绝对差。
我们添加了一个粗略而有效的约束,以防止导致“ NA”值的参数值:目标函数返回较大的正值。我们将其最小化,因此产生NA值的参数被标记为不良。在第一个示例中,我们将数据设置如下:
> data <- list(yM = yM, tm = tm, model = NS, ww = 0.1, min = c( 0,-15,-30, 0), max = c(15, 30, 30,10)) 我们添加了一个模型(在本例中为NS),该模型描述了从参数到收益曲线的映射,以及向量min和max,我们稍后将其用作约束。ww是惩罚权重,如下所述。
OF将采用候选解决方案参数,通过data $ model将此解决方案转换为收益,并将这些收益与yM进行比较,这意味着要计算最大绝对差。
> OF(param2, data) ## 给出正值
[1] 0.97686我们还可以根据收益率曲线比较解决方案。
> par(ps = 11, bty = "n", las = 1, tck = 0.01, mgp = c(3, 0.2, 0), mar = c(4, 4, 1, 1))
> plot(tm, yM, xlab = "maturities in years", ylab = "yields in %")
> lines(tm, NS(param1, tm), col = "blue")
> lines(tm, NS(param2, tm), col = "red")
> legend(x = "topright", legend = c("true yields", "param1", "param2"), col = c("black", "blue", "red"), pch = c(1, NA, NA), lty = c(0, 1, 1))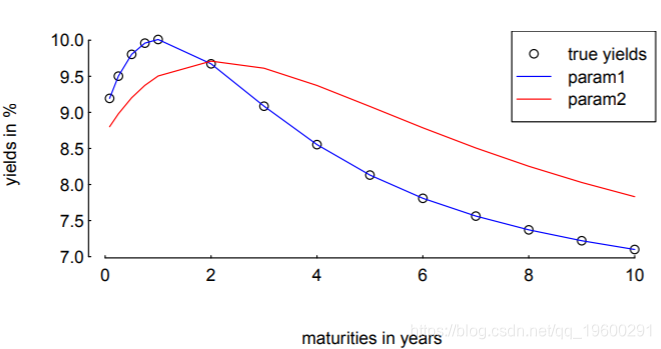
我们通常希望获取参数,以便满足某些约束条件。我们通过惩罚函数将它们包括在内。
我们已经有了数据,因此让我们看看该函数对违反约束的解决方案有何作用。假设我们有三个解的总体mP。
> param1 <- c( 6, 3, 8, -1)
> param2 <- c( 6, 3, 8, 1)
> param3 <- c(-1, 3, 8, 1)
> mP <- cbind(param1,param2,param3)
> rownames(mP) <- c("b1","b2","b3","lambda")
> mP
param1 param2 param3
b1 6 6 -1
b2 3 3 3
b3 8 8 8
lambda -1 1 1第一个和第三个解决方案违反了约束。在第一个解决方案中,λ为负。在第三个解中,β1为负。
> penalty(mP,data)
param1 param2 param3
0.2 0.0 0.2参数ww控制了我们的惩罚程度。
> data$ww <- 0.5
> penalty(mP,data)
param1 param2 param3
1 0 1
对于有效的解决方案,惩罚应为零。
> penalty(mP, data)param1 param2 param30 0 0
请注意,惩罚会立即生效;无需遍历解决方案。
这样我们就可以进行测试了。我们首先定义DE的参数。请特别注意,我们传递了惩罚函数,并将loopPen设置为FALSE。
然后使用目标函数OF,列表数据和列表算法调用DEopt。
> sol <- DEopt(OF = OF, algo = algo, data = data)
差异演化。
最佳解的目标函数值为0;
最终人群中OF的标准偏差为3.0455e-16。
为了检查目标函数是否正常工作,我们将最大误差与返回的目标函数值进行比较–它们应该相同。
> max( abs(data$model(sol$xbest, tm) - data$model(betaTRUE, tm)) )
[1] 0
> sol$OFvalue
[1] 0
作为基准,我们从stats包运行函数nlminb。
如果发现它的性能优于DE,我们将有力地表明我们的DE实现存在问题。
我们使用一个随机起始值s0。
> s0 <- algo$min + (algo$max - algo$min) * runif(length(algo$min))
> sol2 <- nlminb(s0, OF, data = data,
lower = data$min,
upper = data$max,
control = list(eval.max = 50000L,
iter.max = 50000L))
同样,我们比较返回的目标函数值和最大误差。
> max( abs(data$model(sol2$par, tm) - data$model(betaTRUE,tm)) )
[1] 1.5787e-07
> sol2$objective
[1] 1.5787e-07
为了比较我们的两个解(DE和nlminb),我们可以将它们与真实的收益率曲线一起绘制。但是必须强调的是,这两种算法的结果都是随机的:对于DE,因为它故意使用随机性;在nlminb的情况下,因为我们随机设置了起始值。为了获得更有意义的结果,我们应该多次运行这两种算法。为了降低插图的构建时间,我们只运行两种方法一次。
> plot(tm, yM, xlab = "maturities in years",
ylab = "yields in %")
> algo$printDetail <- FALSE
> for (i in seq_len(nRuns)) {
sol <- DEopt(OF = OF, algo = algo, data = data)
lines(tm, data$model(sol$xbest,tm), col = "blue")
s0 <- algo$min + (algo$max-algo$min) * runif(length(algo$min))
sol2 <- nlminb(s0, OF, data = data,
lower = data$min,
upper = data$max,
control = list(eval.max = 50000L,
iter.max = 50000L))
lines(tm,data$model(sol2$par,tm), col = "darkgreen", lty = 2)
}
> legend(x = "topright", legend = c("true yields", "DE", "nlminb"),
col = c("black","blue","darkgreen"),
pch = c(1, NA, NA), lty = c(0, 1, 2))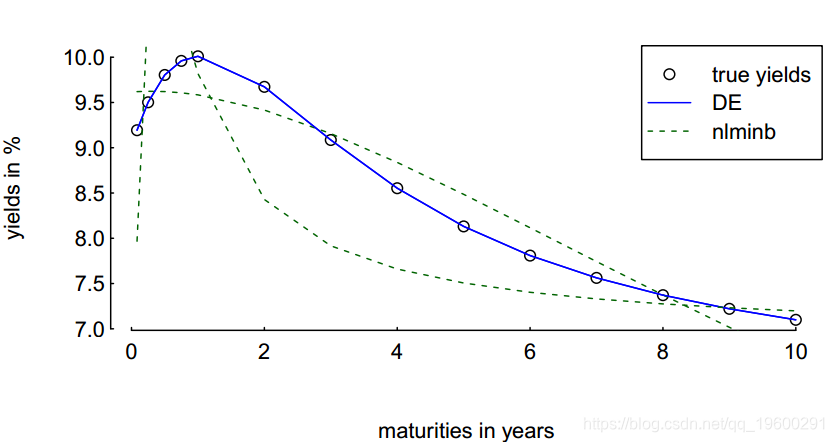
毫无疑问,DE似乎通常只有一条曲线:实际上有nRuns 条线,但是它们是相互叠加的。
其他约束
NS(和NSS)模型的参数约束是要确保所得的零利率为非负数。但实际上,它们不能保证正利率。
> plot(tm, yM, xlab = "maturities in years", ylab = "yields in %")
> abline(h = 0)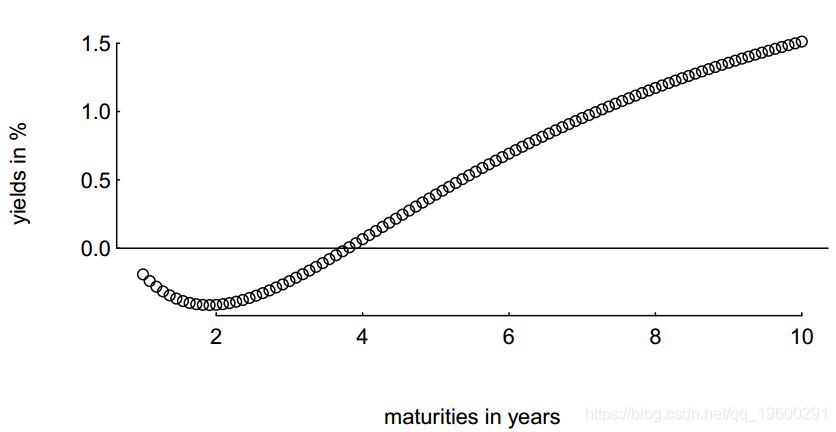
这确实是一个虚构的示例,但尽管如此,我们仍可能希望包括针对此类参数向量的约束措施:我们可以仅包含一个所有速率均大于零的约束条件。
同样,这可以通过惩罚函数来完成。
校验:
> penalty2(c(3, -2, -8, 1.5),data)
[1] 0.86343
此惩罚函数仅适用于单个解决方案,因此实际上将其直接写入目标函数最简单。
因此,就像一个数值测试:假设上述参数为真,而利率为负。
> algo$pen <- NULL; data$yM <- yM; data$tm <- tm
> par(ps = 11, bty = "n", las = 1, tck = 0.01,
mgp = c(3, 0.2, 0), mar = c(4, 4, 1, 1))
> plot(tm, yM, xlab = "maturities in years", ylab = "yields in %")
> abline(h = 0)
> sol <- DEopt(OF = OFa, algo = algo, data = data)
> lines(tm,data$model(sol$xbest,tm), col = "blue")
> legend(x = "topleft", legend = c("true yields", "DE (constrained)"),
col = c("black", "blue"),
pch = c(1, NA, NA), lty = c(0, 1, 2))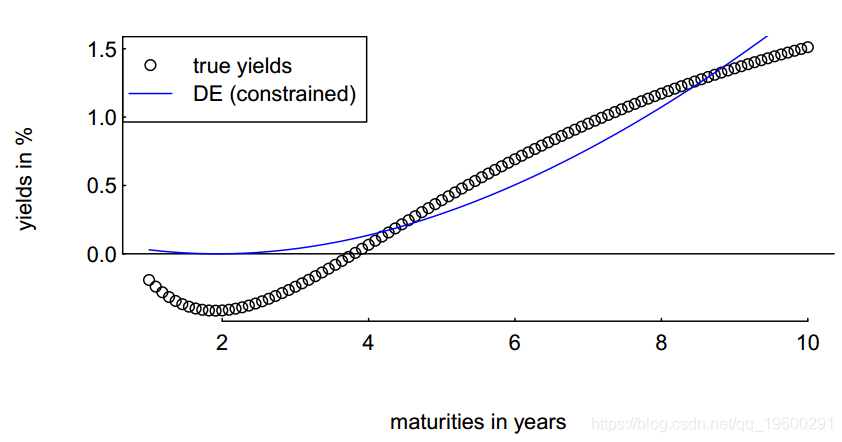
将NSS模型拟合到给定的零利率
如果要改用NSS模型,则几乎不需要更改。我们只需要向目标函数传递一个不同的模型。下面是一个示例。同样,我们修复了真实参数并尝试恢复它们。
列表数据和算法与以前几乎相同;目标函数保持完全相同。
仍然需要运行算法。(同样,我们检查返回的目标函数值。)
> sol <- DEopt(OF = OF, algo = algo, data = data)
> max( abs(data$model(sol$xbest, tm) - data$model(betaTRUE, tm)) )
[1] 7.9936e-15
> sol$OFvalue
[1] 7.9936e-15
我们将结果与nlminb进行比较。
最后,我们比较了几次运行所得的收益率曲线。
> par(ps = 11, bty = "n", las = 1, tck = 0.01,
mgp = c(3, 0.2, 0), mar = c(4, 4, 1, 1))
> plot(tm, yM, xlab = "maturities in years", ylab = "yields in %")
> for (i in seq_len(nRuns)) {
sol <- DEopt(OF = OF, algo = algo, data = data)
lines(tm, data$model(sol$xbest,tm), col = "blue")
s0 <- algo$min + (algo$max - algo$min) * runif(length(algo$min))
sol2 <- nlminb(s0, OF, data = data,
lower = data$min,
upper = data$max,
control = list(eval.max = 50000L,
iter.max = 50000L))
lines(tm, data$model(sol2$par,tm), col = "darkgreen", lty = 2)
}
> legend(x = "topright", legend = c("true yields", "DE", "nlminb"),
col = c("black","blue","darkgreen"),
pch = c(1,NA,NA), lty = c(0,1,2), bg = "white")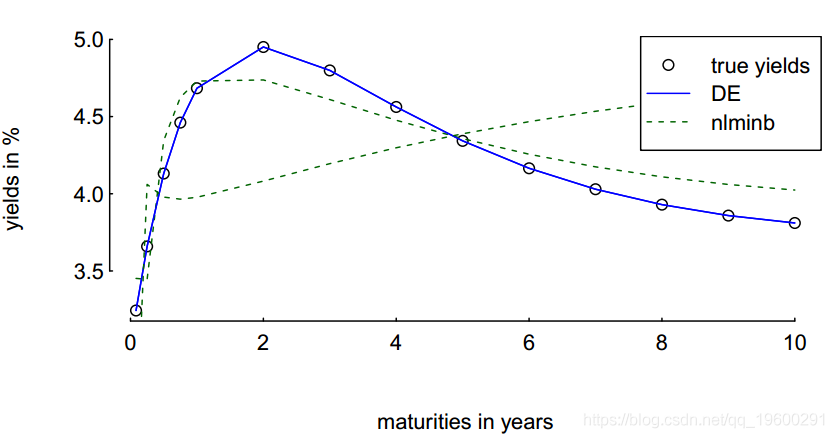
参考文献
关于数值优化中“良好起始值”的注释,2010年。http://comisef.eu/?q = working_papers
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

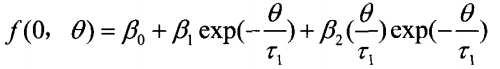
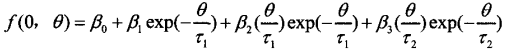
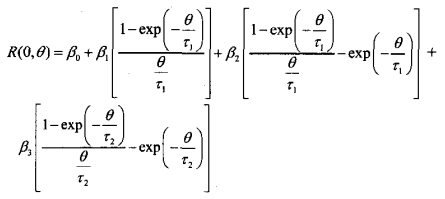

 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python电动汽车充电网络优化研究——泊松过程、排队、贪心算法、模拟退火、聚类、差分演化DE、双目标动态规划、滚动时域预测控制MPC分析储能调度、电网负荷数据|附代码数据
Python电动汽车充电网络优化研究——泊松过程、排队、贪心算法、模拟退火、聚类、差分演化DE、双目标动态规划、滚动时域预测控制MPC分析储能调度、电网负荷数据|附代码数据 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析



