R语言自定义两种统计量度：平均值和中位数，何时去使用？

 但是，在许多应用程序中，考虑到手头的数据，考虑两种方法中的哪一种更为合适是很有用的。在这篇文章中，我们将研究这两个数量之间的差异，并提供建议。

均值

算术平均数是大多数人简单地称为  平均值。但是，确切地说，我们必须注意，平均值只是平均值的一种类型。在迷失于这些术语的复杂性之前，让我们继续进行均值的定义

均值定义为

​

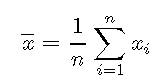
假设我们有x =（30,25,40,41,30,41,50,33,40,1000）x =（30,25,40,41,30,41,50,33,40,1000），这是什么意思？我们可以通过以下方式进行计算：

x <- c(30, 25, 40, 41, 30, 41, 50, 33, 40, 1000)
# the way of the beginner (don't do this!):
x.mean <- 0
for (xi in x) {
    x.mean <- x.mean + xi
}
x.mean <- x.mean / length(x)
print(x.mean)

## [1] 133

# a better way:  
x.mean <- sum(x) / length(x)
print(x.mean)

## [1] 133

# the right way:
x.mean <- mean(x)
print(x.mean)

## [1] 133

可以简单地使用  mean 函数，而不必自己实现均值。

中位数

中位数是指数字列表中最中心的值。尽管很容易解释，但中位数比平均值更难计算。这是因为为了找到中位数，必须对列表中的数字进行排序。此外，我们必须区分两种情况。如果列表中元素的数量为奇数，则中位数是列表中最中心的成员。但是，如果列表中有偶数个元素，则需要确定两个最中心的数字的算术平均值。

我们可以通过以下方式对此进行形式化。令xx为数字的排序向量。那么中位数是

​

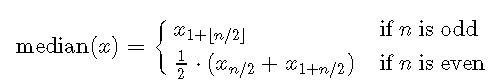
让我们看看如何获​​得R中的中位数。

x.median <- mymedian(x)
print(x.median)

## [1] 40

# the easy way:
x.median <- median(x)
print(x.median)

## [1] 40

均值和中位数的比较

定义了两种类型的平均值之后，我们现在可以研究两者之间的差异。尽管算术平均值考虑   了向量中的所有值，但中值仅考虑了 值的  子集。这是因为中位数基本上丢弃了除最中心值以外的所有矢量元素。中位数的此功能可能会有很大的不同。正如我们在示例中所看到的，xx的平均值（133）远大于其中位数（40）。在这种情况下，这是因为中位数会丢弃xx中的值1000，而算术平均值会考虑它。

这使我们想到了我们要回答的问题：何时使用均值以及何时使用中位数？答案很简单。如果您的数据包含离群值（例如在我们的示例中为1000），那么 通常宁愿使用中位数，因为平均值的值将由离群值而不是典型值主导。总之，如果 正在考虑均值，请检查数据是否存在异常值。一种简单的方法是绘制数据的直方图。

​

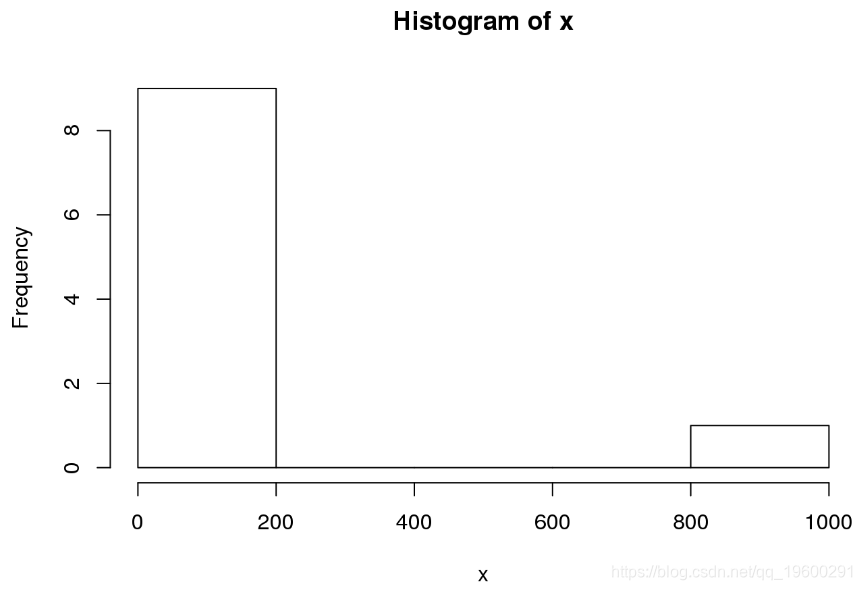
对于我们的数据，直方图清楚地显示了值为1000的离群值，我们得出的结论是，中位数比平均值更合适。