了解不同的市场状况如何影响您的策略表现可能会对您的收益产生巨大的影响。
某些策略在波动剧烈的市场中表现良好，而其他策略则需要强劲而平稳的趋势，否则将面临长时间的下跌风险。
可下载资源
搞清楚什么时候开始或停止交易策略，调整风险和资金管理技巧，甚至设置进入和退出条件的参数都取决于市场“状态”或当前的情况。
能够识别不同的市场状态并相应地改变您的策略可能意味着市场成功和失败之间的区别。在本文中，我们将探讨如何通过使用一种强大的机器学习算法来识别不同的市场区制（机制），称为“隐马尔可夫模型”。
隐马尔可夫模型(Hidden Markov model, HMM)是一种结构最简单的动态贝叶斯网的生成模型，它也是一种著名的有向图模型。它是典型的自然语言中处理标注问题的统计机器学模型，本文将重点介绍这种经典的机器学习模型。
一、引言
假设有三个不同的骰子(6面、4面、8面)，每次先从三个骰子里面选择一个，每个骰子选中的概率为1/3，如下图所示，重复上述过程，得到一串数值[1,6,3,5,2,7]。这些可观测变量组成可观测状态链。同时，在隐马尔可夫模型中还有一条由隐变量组成的隐含状态链，在本例中即骰子的序列。比如得到这串数字骰子的序列可能为[D6, D8, D8, D6, D4, D8]。
隐马尔可夫型示意图如下所示：
图中，箭头表示变量之间的依赖关系。图中各箭头的说明如下：
在任意时刻，观测变量(骰子)仅依赖于状态变量(哪类骰子)，同时t时刻的状态qt仅依赖于t-1时刻的状态qt-1。这就是马尔科夫链，即系统的下一时刻仅由当前状态（无记忆），即“齐次马尔可夫性假设”
二、隐马尔可夫模型的定义
根据上面的例子，这里给出隐马尔可夫的定义。隐马尔科夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个可观测的随机序列的过程，隐藏的马尔可夫链随机生成的状态序列，称为状态序列(也就上面例子中的D6，D8等)；每个状态生成一个观测，而由此产生的观测随机序列，称为观测序列(也就上面例子中的1，6等)。序列的每个位置又可以看作是一个时刻。
隐马尔可夫模型由初始的概率分布、状态转移概率分布以及观测概率分布确定。具体的形式如下，这里设Q是所有可能的状态的集合，V是所有可能的观测的集合，即有：
其中，N是可能的状态数，M是可能观测的数。另外设I是长度为T的状态序列，O是对应的观测序列：
在马尔可夫链中，有几个矩阵变量，分别是状态转移概率矩阵A，观测概率矩阵B，以及初始状态概率向量C，其中状态转移概率矩阵A为：
其中，
是在时刻t处于状态qi的条件下生成状态qj的概率。
初始状态概率向量为：
Ci为时刻t=1处于状态qi的概率。
隐马尔可夫模型由初始状态概率向量C，状态转移概率矩阵A和观测概率矩阵B决定，C和A决定状态序列，B决定观测序列，因此隐马尔可夫模型可以用三元符号表示为：
A、B和C也被称为隐马尔科夫模型的三要素。
状态转移概率矩阵A与初始状态概率向量C确定了隐藏的马尔可夫链，生成不可观测的状态序列，观测概率矩阵B确定了如何从状态生成观测，与状态序列综合确定了如何产生观测序列。
从定义中，可以发现隐马尔可夫模型作了两个基本假设：
(1) 马尔可夫性假设，即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态，与其它时刻的状态及观测无关，也与时刻t无关，
(2) 观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关。
隐马尔可夫模型可以用于标注，这时状态对应着标记，标注问题是给定观测的序列预测其对应的标记序列。可以假设标注问题的数据是由隐马尔可夫模型生成的，这样可以利用该模型的学习与预测算法进行标注。
隐马尔科夫模型的三个基本问题：
(1) 概率计算问题：给定模型lamda=(A,B,C)和观测序列O=(o1,o2,…,oT)，计算在该模型下观测序列O出现的概率P(O|lamda)。
(2) 学习问题：一直观测序列O=(o1,o2,…,oT)，估计模型lamda=(A,B,C)参数，使得在该模型下观测序列概率P(O|lamda)最大，即用极大似然估计的方法估计参数。
(3) 预测问题，也称为解码的问题，已知模型lamda=(A,B,C)和观测序列O=(o1,o2,…,oT)，求对给定观测序列条件概率P(I|O)最大的状态序列 I = (i1,i2,…,iT)，即给定观测序列，求最有可能的对应的状态序列。
三、前向算法
在介绍前向算法之前，先介绍前向概率。
前向概率：在给定隐马尔科夫模型lamda，定义到时刻t部分观测序列为o1,o2,…,ot且状态为qi的概率为前向概率，记为：
可以根据数据对前向概率公式进行递推，并最终得到观测序列概率P(O|lamda). 前向概率算法就是根据前向概率递推公式进行计算的，输入为隐马尔可夫模型和观测序列，输出的结果为序列概率P(O|lamda). 计算的步骤为：
(1) 根据前向概率公式，先设定 t = 1的初值：
(2) 根据前向概率公式对前向概率进行递推，因此对t=1,2,…,N-1有：
(3) 最后对所有的前向概率进行求和得到最终的结果，即为：
该算法所表示的递推关系图为：
对于步骤一的初始，是初始时刻的状态i1 = q1和观测o1的联合概率。步骤(2) 是前向概率的递推公式，计算到时刻t+1部分观测序列为o1,o2,…,ot,ot+1 且在时刻t+1处于状态qi的前向概率。如上图所示，既然at(j)是得到时刻t观测到o1,o2,…,ot并在时刻t处于状态的qj前向概率，那么at(j)aji就是到时刻t观测到o1,o2,…,ot并在是时刻t处于qj状态而在时刻t+1到达qi状态的联合概率。对于这个乘积在时刻t的所有可能的N个状态求和，其结果就是到时刻t观测为o1,o2,…,ot，并在时刻t+1处于状态qi的联合概率。最后第三步，计算出P(O|lamda)的结果。
当然这里只是介绍了诸多算法中的一种，类似的还有后向算法(大家可以看相关的书籍进行了解)。对于动态规划的解决隐马尔科夫模型预测问题，应用最多的是维特比算法
隐马尔可夫模型
马尔科夫模型是一个概率过程，看当前的状态来预测下一个状态。一个简单的例子就是看天气。假设我们有三个天气条件（也称为区制或机制）：多雨，阴天，晴天。如果今天下雨，马尔可夫模型寻找每个不同的天气情况发生的概率。例如，明天可能继续下雨的概率较高，多云的可能性略低，晴天可能性较小。
今天的天气明天的天气变化的概率
多雨的多雨的65％
多雨的多云的25％
多雨的晴朗10％
多云的多雨的55％
多云的多云的20％
多云的晴朗25％
晴朗多雨的10％
晴朗多云的30％
晴朗晴朗60％
这似乎是一个非常简单的过程，但其复杂性在于不知道每个状态转移的概率，以及如何解释这些随时间变化的概率。这就是隐马尔可夫模型（HMM）发挥作用的地方。他们能够估计每个状态的转移概率，然后根据目前的情况输出最可能的状态。
我们可以将市场定义为看涨，看跌，平稳，或者波动率高或者低，或者我们知道的一些因素的综合影响我们的策略的表现，而不是天气条件。
构建真实数据模型
我们正在寻找基于这些因素的不同的市场机制，然后我们可以用它来优化我们的交易策略。为此，我们将使用EUR / USD数据来构建模型。
首先，构建我们的数据集。
ModelData <-data.frame（LogReturns，ATR）#为我们的HMM模型创建数据
ModelData <-ModelData [-c（1:14），]#删除计算指标数据
colnames（ModelData）< - c（"LogReturns"，"ATR"）#命名我们的列我们将对数收益率和ATR设置为我们的因变量。使用我们刚刚构建的数据框，要设置3个不同的状态，并将因变量分布设置为高斯分布。
HMMfit <-fit（HMM，verbose = FALSE）#将我们的模型添加到数据集中
转移矩阵给了我们从一个状态动到下一个状态的概率。
HMMpost <-posterior（HMMfit）#查找我们的数据集中每个状态的后验概率
我们可以看到，我们现在有每个状态的概率以及最高概率类别。
让我们看看发现了什么：
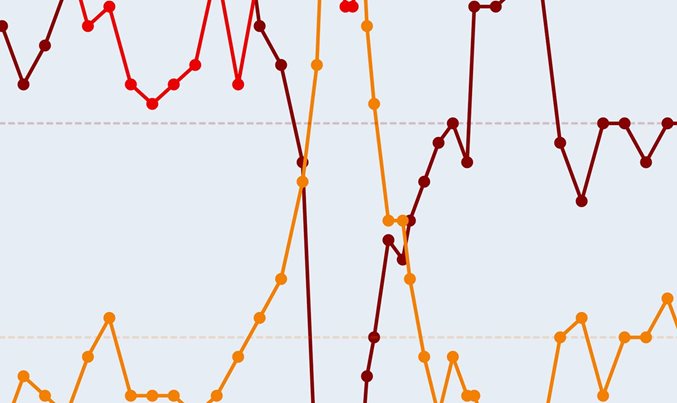
每个状态的概率：
随时关注您喜欢的主题
我们可以看到，状态3往往是高波动和大幅度波动的时期，状态2的特点是中等波动，状态1是低波动的。
隐马尔可夫模型是强大的工具，可以让你洞察不断变化的市场状态。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
Python用Markov RNN马尔可夫递归神经网络建模序列数据t-SNE可视化研究
