向量自回归(VAR)模型的一般缺点是,估计系数的数量与滞后的数量成比例地增加。
因此,随着滞后次数的增加,每个参数可用的信息较少。
在贝叶斯VAR文献中,减轻这种所谓_的维数诅咒的_一种方法是_随机搜索变量选择_(SSVS),由George等人提出(2008)。
向量自回归(VAR)模型不是具备经济学理论基础的结构化计量经济模型, 而是非结构化的时间序列模型。具体而言,VAR模型选择一组关联性较高的内生 经济变量组成一个向量,通过多阶滞后回归来估计各变量之间的关系,从而得到 相关经济变量的预测模型。常见的非限制性VAR模型存在一些明显缺陷:VAR模 型忽略了先验信息,并对所有要估计的参数都预设了相同的重要性,这可能引发 实证研究采用错误的模型;非限制性VAR模型需要估计过多的参数,导致“过参 数化”的情况比较严重,同时,由于宏观经济数据时间序列一般都较短,整个 VAR预测系统的自由度不足、稳健性较差。
Litterman (1986)提出的贝叶斯向量自回归模型(BVAR)是VAR模型的一 个扩展。遵循贝叶斯统计思想,BVAR模型假设系数矩阵中各元素分别满足某一 先验分布,通过设置系数矩阵中各元素的数学期望和标准差的变动范围,控制各 经济变量对整个预测系统的影响,从而达到降低预测误差、提高系统预测精度的目的。
SSVS的基本思想是将通常使用的先验方差分配给应包含在模型中的参数,将不相关参数的先验方差接近零。
这样,通常就可以估算出相关参数,并且无关变量的后验值接近于零,因此它们对预测和冲激响应没有显着影响。这是通过在模型之前添加层次结构来实现的,其中在采样算法的每个步骤中评估变量的相关性。
这篇文章介绍了使用SSVS估计贝叶斯向量自回归(BVAR)模型。它使用Lütkepohl(2007)的数据集E1,其中包含有关1960Q1至1982Q4德国固定投资,可支配收入和消费支出的数据。加载数据并生成数据:
# 加载和转换数据
e1 <- diff(log(e1))
# 生成VAR
data <- gen_var(e1, p = 4, deterministic = "const")
# 获取数据矩阵
y <- data$Y[, 1:71]
x <- data$Z[, 1:71]估算值
根据George等人所述的半自动方法来设置参数的先验方差(2008)。对于所有变量,先验包含概率设置为0.5。误差方差-协方差矩阵的先验信息不足。
# 重置随机数提高可重复性
set.seed(1234567)
t <- ncol(y) # 观察数
k <- nrow(y) # 内生变量数
m <- k * nrow(x) # 估计系数数
# 系数先验
a_mu_prior <- matrix(0, m) # 先验均值的向量
# SSVS先验(半自动方法)
ols <- tcrossprod(y, x) %*% solve(tcrossprod(x)) # OLS估计
sigma_ols <- tcrossprod(y - ols %*% x) / (t - nrow(x)) # OLS误差协方差矩阵
cov_ols <- kronecker(solve(tcrossprod(x)), sigma_ols)
se_ols <- matrix(sqrt(diag(cov_ols))) # OLS标准误
# 先验参数
prob_prior <- matrix(0.5, m)
# 方差-协方差矩阵
u_sigma_df_prior <- 0 # 方差-协方差矩阵
u_sigma_scale_prior <- diag(0, k) # 先验协方差矩阵
u_sigma_df_post <- t + u_sigma_df_prior # 后验自由度初始参数值设置为零,这意味着在Gibbs采样器的第一步中应相对自由地估算所有参数。
可以直接将SSVS添加到VAR模型的标准Gibbs采样器算法中。在此示例中,常数项从SSVS中排除,这可以通过指定来实现include = 1:36。具有SSVS的Gibbs采样器的输出可以用通常的方式进一步分析。因此,可以通过计算参数的绘制方式获得点估计:
## invest income cons
## invest.1 -0.102 0.011 -0.002
## income.1 0.044 -0.031 0.168
## cons.1 0.074 0.140 -0.287
## invest.2 -0.013 0.002 0.004
## income.2 0.015 0.004 0.315
## cons.2 0.027 -0.001 0.006
## invest.3 0.033 0.000 0.000
## income.3 -0.008 0.021 0.013
## cons.3 -0.043 0.007 0.019
## invest.4 0.250 0.001 -0.005
## income.4 -0.064 -0.010 0.025
## cons.4 -0.023 0.001 0.000
## const 0.014 0.017 0.014 随时关注您喜欢的主题
还可以通过计算变量的均值来获得每个变量的后验概率。从下面的输出中可以看出,在VAR(4)模型中似乎只有几个变量是相关的。常数项的概率为100%,因为它们已从SSVS中排除。
## invest income cons
## invest.1 0.43 0.23 0.10
## income.1 0.10 0.18 0.67
## cons.1 0.11 0.40 0.77
## invest.2 0.11 0.09 0.14
## income.2 0.08 0.07 0.98
## cons.2 0.07 0.06 0.08
## invest.3 0.19 0.07 0.06
## income.3 0.06 0.13 0.10
## cons.3 0.09 0.07 0.12
## invest.4 0.78 0.09 0.16
## income.4 0.13 0.09 0.18
## cons.4 0.09 0.07 0.06
## const 1.00 1.00 1.00 给定这些值,研究人员可以按照常规方式进行操作,并根据Gibbs采样器的输出获得预测和脉冲响应。这种方法的优势在于它不仅考虑了参数不确定性,而且还考虑了模型不确定性。
hist(draws_a[6,], 这可以通过系数的直方图来说明,该直方图描述了收入的第一个滞后项与消费当前值之间的关系。
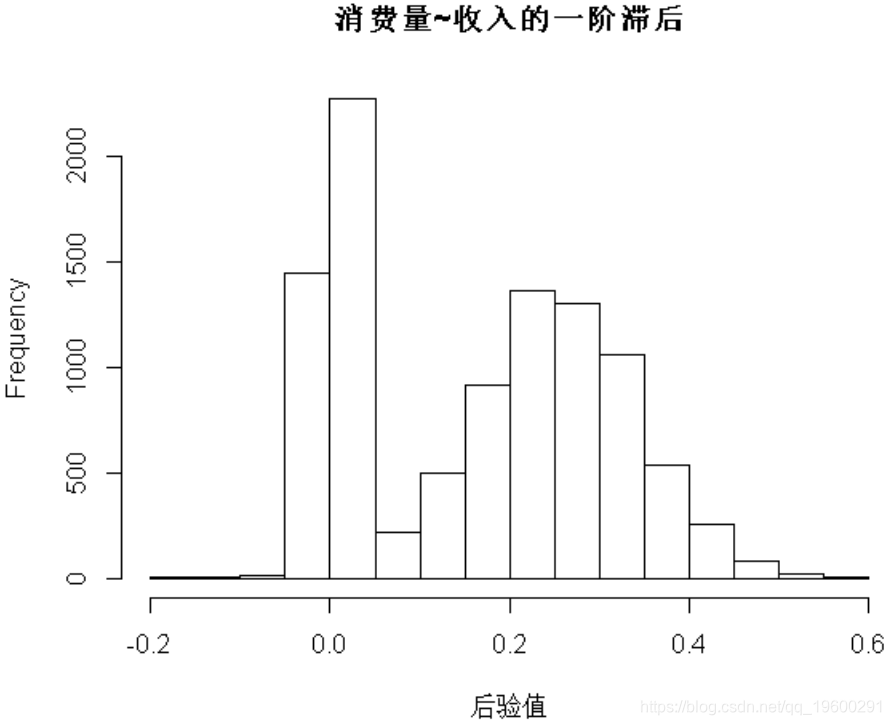
通过两个峰描述模型不确定性,并通过右峰在它们周围的分布来描述参数不确定性。
但是,如果研究人员不希望使用模型,变量的相关性可能会从采样算法的一个步骤更改为另一个步骤,那么另一种方法将是仅使用高概率的模型。这可以通过进一步的模拟来完成,在该模拟中,对于不相关的变量使用非常严格的先验,而对于相关参数则使用没有信息的先验。
后方抽取的均值类似于Lütkepohl(2007,5.2.10节)中的OLS估计值:
## invest income cons
## invest.1 -0.219 0.001 -0.001
## income.1 0.000 0.000 0.262
## cons.1 0.000 0.238 -0.334
## invest.2 0.000 0.000 0.001
## income.2 0.000 0.000 0.329
## cons.2 0.000 0.000 0.000
## invest.3 0.000 0.000 0.000
## income.3 0.000 0.000 0.000
## cons.3 0.000 0.000 0.000
## invest.4 0.328 0.000 -0.001
## income.4 0.000 0.000 0.000
## cons.4 0.000 0.000 0.000
## const 0.015 0.015 0.014 bvar功能可用于将Gibbs采样器的相关输出收集到标准化对象中,例如predict获得预测或irf进行脉冲响应分析。
评价
hin(bvar_est, thin = 5) 预测
可以使用函数获得置信区间的预测predict。
plot(bvar_pred)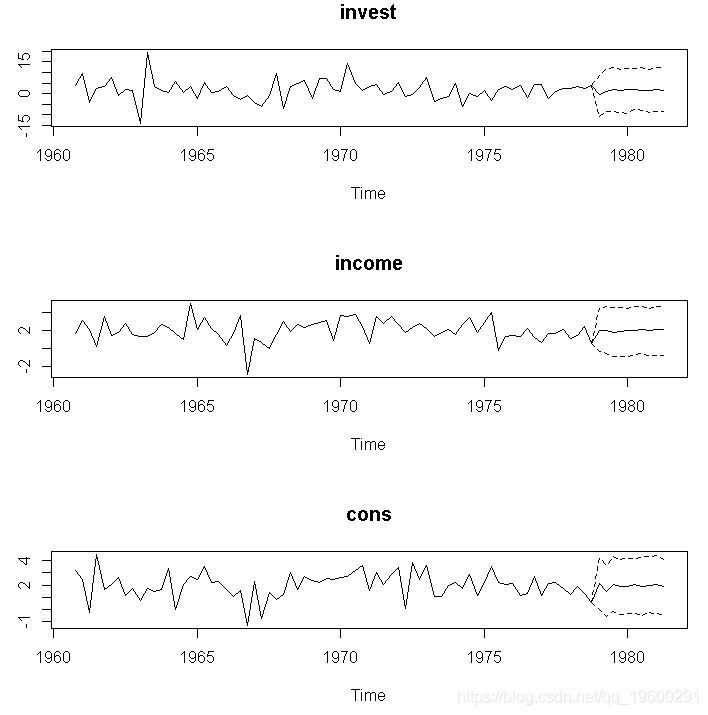
脉冲响应分析
plot(OIR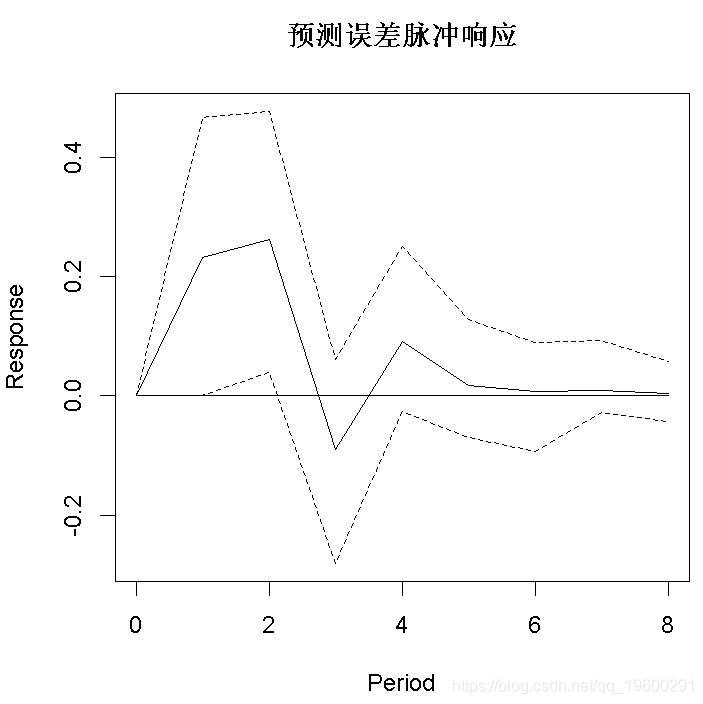
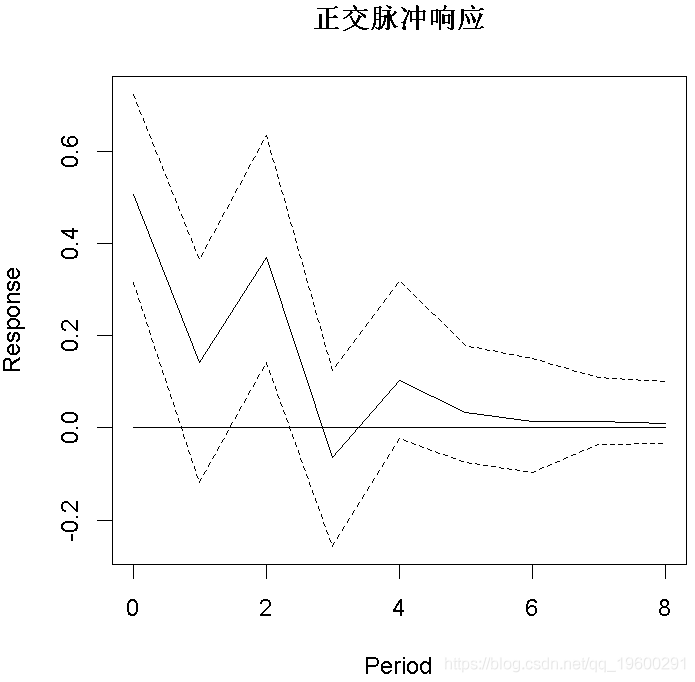
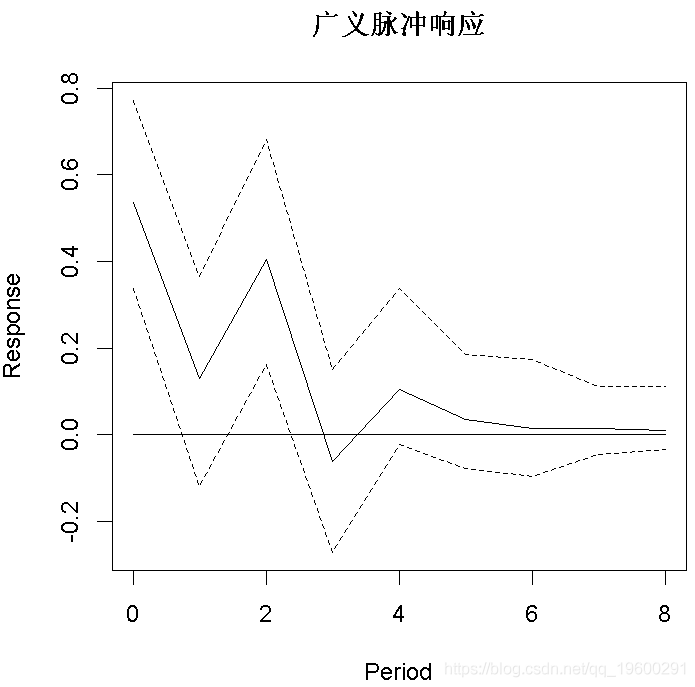
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据 【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用
【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用 视频讲解|核密度估计朴素贝叶斯:业务数据分类—从理论到实践
视频讲解|核密度估计朴素贝叶斯:业务数据分类—从理论到实践




3 comments on “R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型”