任何时间序列都可以表示为在 谐波 频率上振荡的余弦和正弦波之和= j / n,其中j = 1,2,…,n / 2。周期图给出了关于各种频率的相对强度的信息,用于解释时间序列的变化。
周期图是称为谱密度 函数的样本估计,其是群体平稳时间序列的频域表征。谱密度是与自协方差时域表示直接相关的时间序列的频域表示。本质上,谱密度和自协方差函数包含相同的信息,但以不同的方式表达。
估计光谱密度的方法
原始周期图是人口谱密度的粗略样本估计。估计是“粗略的”,部分是因为我们只使用离散的基波谐波频率用于周期图,而频谱密度是在连续的频率上定义的。
平滑方法(光谱密度的非参数估计)
在R中,可以使用命令kernel 生成m = 2 的Daniell内核的加权系数。 结果是
coef [-2] = 0.2
coef [-1] = 0.2
coef [0] = 0.2
coef [1] = 0.2
coef [2] = 0.2
coef []的下标是指与时间t的平均值中心的时差。
在R中,命令 (“daniell”,c(2,2))将提供系数,这些系数将作为权重应用于对两个平滑中m = 2 的回旋Daniell内核的原始数据值求平均值。结果是
coef [-4] = 0.04
coef [-3] = 0.08
coef [-2] = 0.12
coef [-1] = 0.16
coef [0] = 0.20
coef [ 1] = 0.16
coef [2] = 0.12
coef [3] = 0.08
coef [4] = 0.04
这会生成平滑公式
^ x t=0.04xt-4+0.08xt-3+0.12xt-2+0.16xt-1+0.20xt+0.16xt+1+0.12xt+2+0.08xt+3+0.04xt+4。x^t=0.04xt−4+0.08xt−3+0.12xt−2+0.16xt−1+0.20xt+0.16xt+1+0.12xt+2+0.08xt+3+0.04xt+4.
命令 (“modified.daniell”,c(2,2)) 给出了这些系数:
coef [-4] = 0.01563
coef [-3] = 0.06250
coef [-2] = 0.12500
coef [-1] = 0.18750
coef [0] = 0.21875
coef [1] = 0.18750
coef [2] = 0.12500
coef [3] = 0.06250
coef [4] = 0.01563
当我们平滑周期图时,我们在频率间隔而不是时间间隔上进行平滑。
带宽
带宽应该足以平滑我们的估计,但是如果我们使用太大的带宽,我们将过多地平滑周期图并且错过看到重要的峰值。在实践中,通常需要一些实验来找到提供合适平滑的带宽。
R代码
使用Daniell内核对周期图进行平均/平滑可以使用两个命令的序列在R中完成。第一个定义了Daniell内核,第二个定义了平滑周期图。
例如,假设观察到的序列被命名为x,我们希望使用具有m = 4的Daniell内核来平滑周期图。命令是
mvspec(x,k,log =“no”)
第一个命令创建平滑所需的加权系数,并将它们存储在名为k的向量中。 第二个命令要求基于系列x的周期图的谱密度估计,使用存储在k中的加权系数,该图将是普通的比例,不是对数刻度。
如果需要卷积,则可以将内核命令修改为类似k = kernel(“daniell”,c(4,4)) 。
例如,m = 4 的修改后的Daniell内核长度L = 2 m +1 = 9,因此我们可以使用该命令
mvspec(x,spans = 9,log =“no”)
可以使用每次通过m = 4 的修改的Daniell内核的两次通过
mvspec(x,spans = c(9,9),log =“no”)
可以使用命令创建原始周期图(或者可以使用第6课中给出的方法创建原始周期图)。
mvspec(x,log =“no”)

请注意,在刚刚给出的命令中,我们省略了为平滑提供权重的参数。
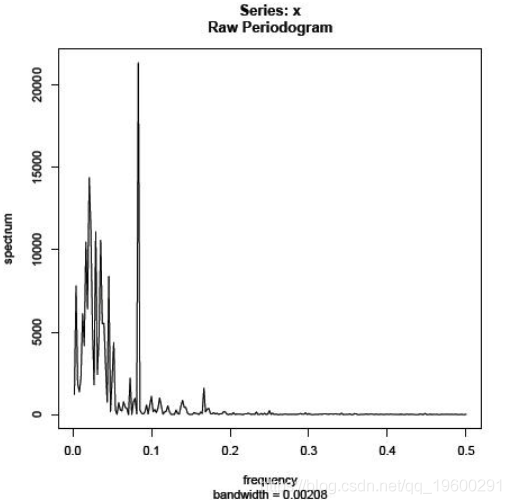

原始周期图如下:
下一个图是使用具有m = 4 的Daniell核的平滑周期图。
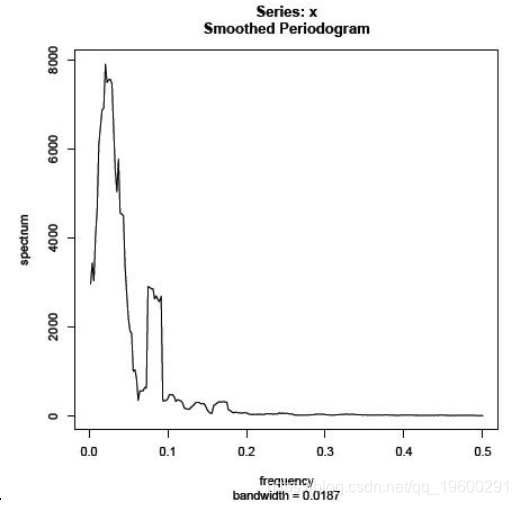

下一个图是一个平滑的周期图,使用Daniell内核的两次传递,每次传递m = 4。请注意它是如何比以前更平滑。
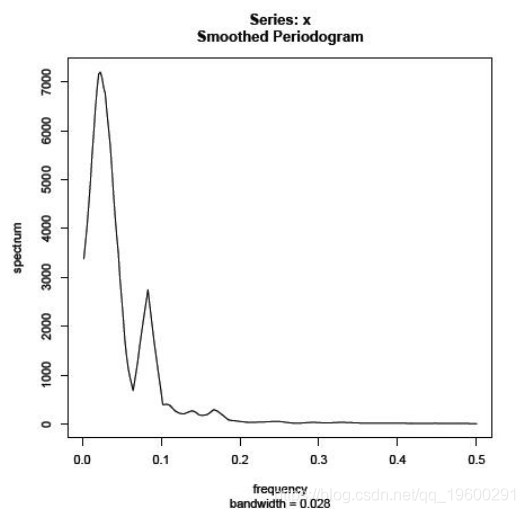

要了解两个主要峰的位置,请为mvspec输出指定一个名称,然后列出它。例如,
specvalues = mvspec(x,k,log =“no”)
specvalues $ spec
您可以筛选输出以查找峰值出现的频率。频率和频谱密度估计单独列出,但顺序相同。确定最大光谱密度,然后找到相应的频率。
这里,第一个峰值的频率≈0208。与此周期相关的周期(月数)= 1 / .0208 = 48个月。第二个峰值出现在频率≈0.083333。相关时期= 1 / .08333 = 12个月。第一个峰值与厄尔尼诺天气效应有关。第二个是通常12个月的季节性影响。
abline(v = 1/44,lty =“dotted”)
abline(v = 1/12,lty =“dotted”)
这是结果图:
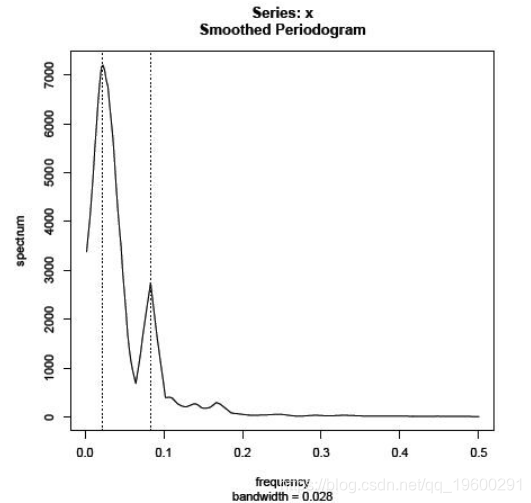

我们已经足够平滑,但出于演示目的,下一个情节是结果
mvspec(x,spans = c(13,13),log =“no”)

这使用两次修改的Daniell内核,每次长度L = 13(所以m = 6)。
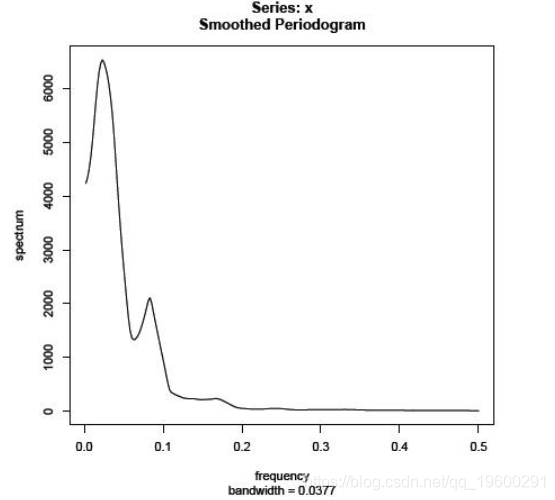

绝对有可能过度平滑。假设我们使用总长度= 73(m = 36)的修改过的Daniell内核。命令是
mvspec(x,spans = 73,log =“no”)

结果如下。高峰消失
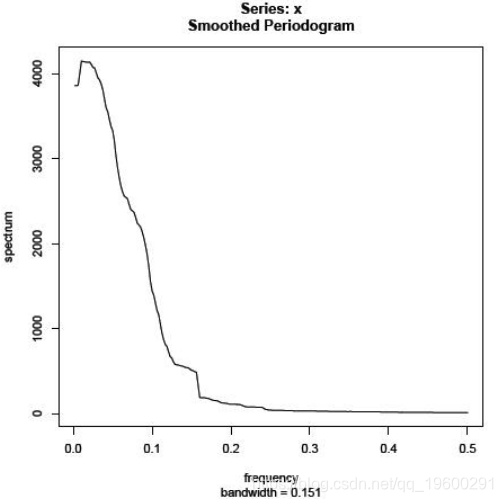

光谱密度的参数估计
谱密度估计的平滑方法称为非参数方法,因为它不使用任何参数模型用于基础时间序列过程。另一种方法是参数方法,该方法需要找到该系列的最佳拟合AR模型,然后绘制该模型的谱密度。
在R中,使用命令/功能spec.ar可以轻松完成谱密度的参数估计。
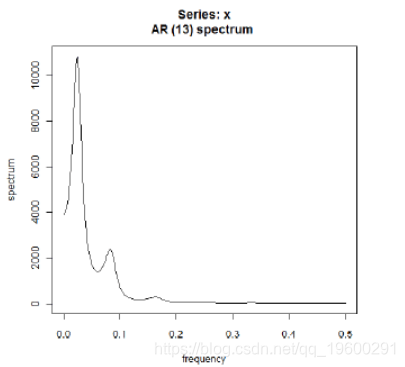

估计的谱密度的出现与以前相同。估计的厄尔尼诺峰位于略微不同的位置 – 频率约为0.024,周期约为1 / 0.024 =约42个月。
平滑器在原始数据中的应用
请注意,此处描述的平滑器也可以应用于原始数据。Daniell内核及其修改只是移动平均(或加权移动平均)平滑器。
非常感谢您阅读本文,有任何问题请在下面留言!
1
1
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据



