标准的ARIMA（移动平均自回归模型）模型允许只根据预测变量的过去值进行预测。
最近我们被客户要求撰写关于ARIMAX模型的研究报告。该模型假定一个变量的未来的值线性地取决于其过去的值，以及过去（随机）影响的值。ARIMAX模型是ARIMA模型的一个扩展版本。它还包括其他独立（预测）变量。该模型也被称为向量ARIMA或动态回归模型。
ARIMAX模型（自回归积分滑动平均模型带外生变量）是在ARIMA模型基础上引入外生变量（解释变量）的扩展模型。它结合了ARIMA模型处理时间序列数据的能力和外生变量回归模型解释变量影响的能力，使得模型可以更全面地考虑时间序列数据的特征和外部因素的影响。本文练习提供了一个进行ARIMAX模型预测的练习。还检查了回归系数的统计学意义。
可下载资源
ARIMAX模型类似于多变量回归模型，但允许利用回归残差中可能存在的自相关来提高预测的准确性。
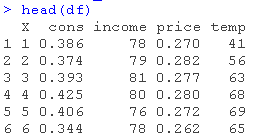
这些练习使用了冰淇淋消费数据。该数据集包含以下变量。
- 美国的冰淇淋消费（人均）
- 每周的平均家庭收入
- 冰淇淋的价格
- 平均温度。
观测数据的数量为30个。它们对应的是1951年3月18日至1953年7月11日这一时间段内的四周时间。
练习1
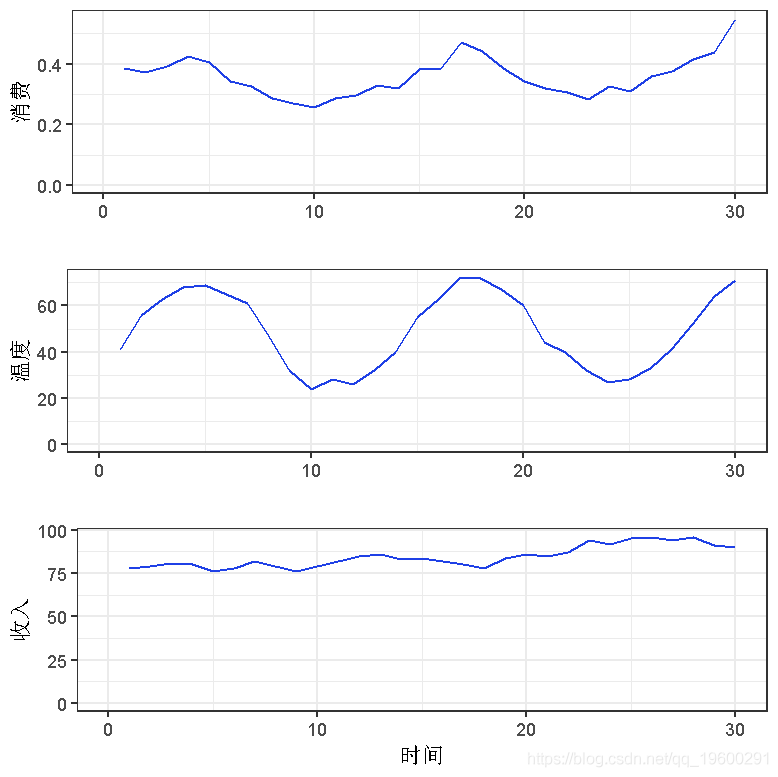
加载数据集，并绘制变量cons（冰淇淋消费）、temp（温度）和收入。
ggplot(df, aes(x = X, y = income)) +
ylab("收入") +
xlab("时间") +
grid.arrange(p1, p2, p3, ncol=1, nrow=3)
练习 2
对冰淇淋消费数据估计ARIMA模型。然后将该模型作为输入传给预测函数，得到未来6个时期的预测数据。
auto.arima(cons)
fcast\_cons <- forecast(fit\_cons, h = 6)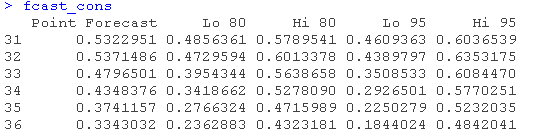
练习3
绘制得到的预测图。
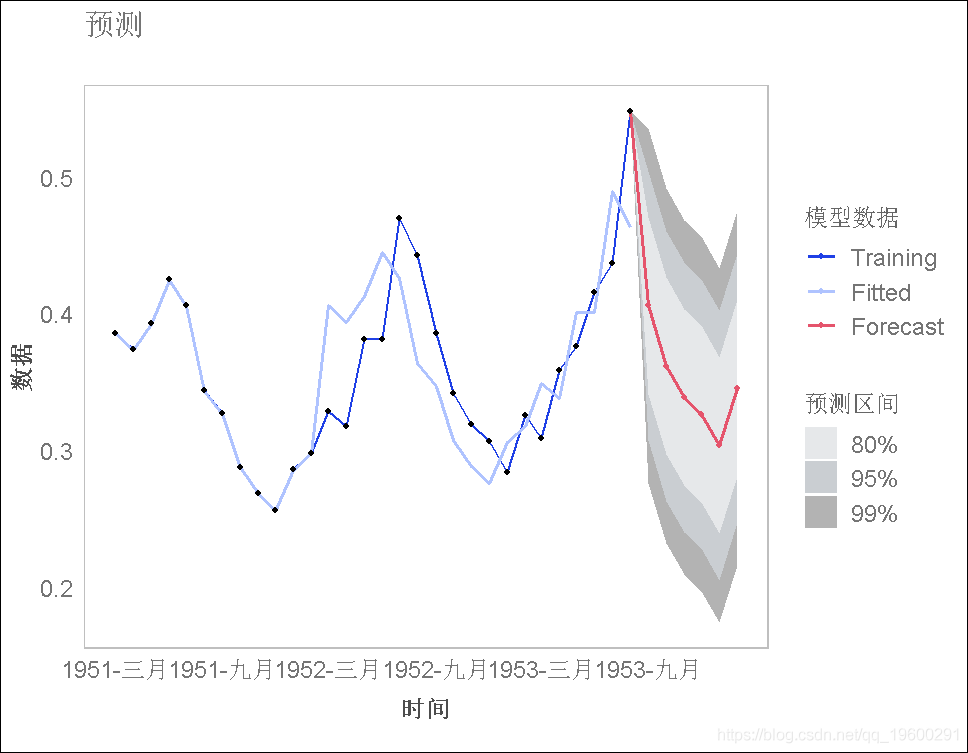
练习4
找出拟合的ARIMA模型的平均绝对误差（MASE）。
accuracy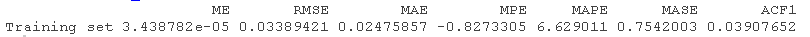
练习5
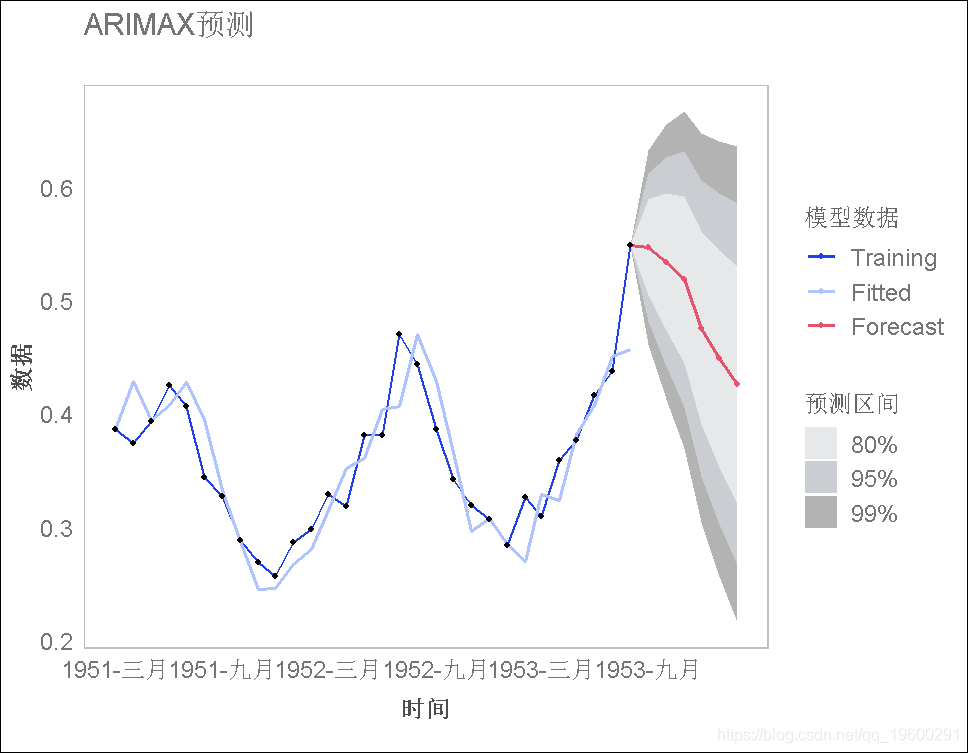
为消费数据估计一个扩展的ARIMA模型，将温度变量作为一个额外的回归因子（使用auto.arima函数）。然后对未来6个时期进行预测（注意这个预测需要对期望温度进行假设；假设未来6个时期的温度将由以下向量表示：
fcast_temp <- c(70.5, 66, 60.5, 45.5, 36, 28)）绘制获得的预测图。
随时关注您喜欢的主题
练习6
输出获得的预测摘要。找出温度变量的系数，它的标准误差，以及预测的MASE。将MASE与初始预测的MASE进行比较。
summary(fca)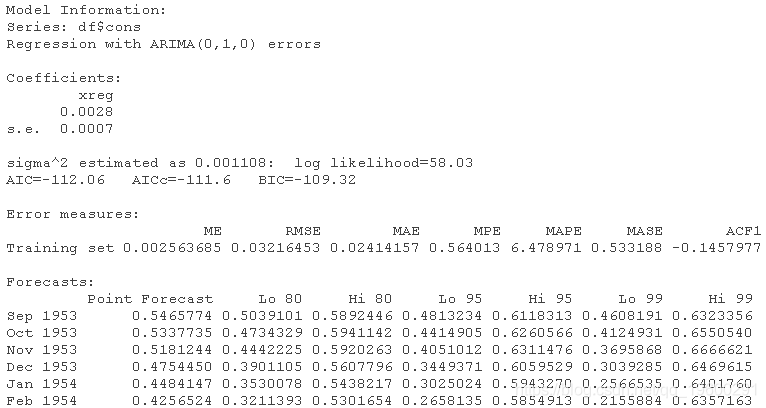
温度变量的系数是0.0028
该系数的标准误差为0.0007
平均绝对比例误差为0.7354048，小于初始模型的误差（0.8200619）。
练习7
检查温度变量系数的统计意义。该系数在5%的水平上是否有统计学意义？
test(fit)
练习8
估计ARIMA模型的函数可以输入更多的附加回归因子，但只能以矩阵的形式输入。创建一个有以下几列的矩阵。
注意：最后三列可以通过在收入变量值的向量中添加两个NA来创建，并将得到的向量作为嵌入函数的输入（维度参数等于要创建的列数）。
温度变量的值。
收入变量的值。
滞后一期的收入变量的值。
滞后两期的收入变量的值。
输出该矩阵。
vars <- cbind(temp, income)
print(vars)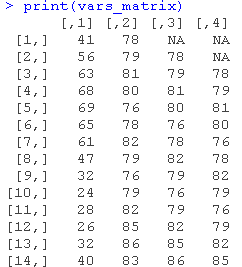
练习9
使用获得的矩阵来拟合三个扩展的ARIMA模型，使用以下变量作为额外的回归因子。
温度、收入。
温度、收入的滞后期为0、1。
温度，滞后期为0、1、2的收入。
检查每个模型的摘要，并找到信息准则（AIC）值最低的模型。
注意AIC不能用于比较具有不同阶数的ARIMA模型，因为观察值的数量不同。例如，非差分模型ARIMA（p，0，q）的AIC值不能与差分模型ARIMA（p，1，q）的相应值进行比较。
auto.arima(cons, xreg = var)
print(fit0$aic)
可以使用AIC，因为各模型的参数阶数相同（0）。
AIC值最低的模型是第一个模型。
它的AIC等于-113.3。
练习10
使用上一练习中发现的模型对未来6个时期进行预测，并绘制预测图。预测需要一个未来6个时期的期望温度和收入的矩阵；使用temp变量和以下期望收入值创建矩阵：91, 91, 93, 96, 96, 96。
找出该模型的平均绝对比例误差，并与本练习集中前两个模型的误差进行比较。
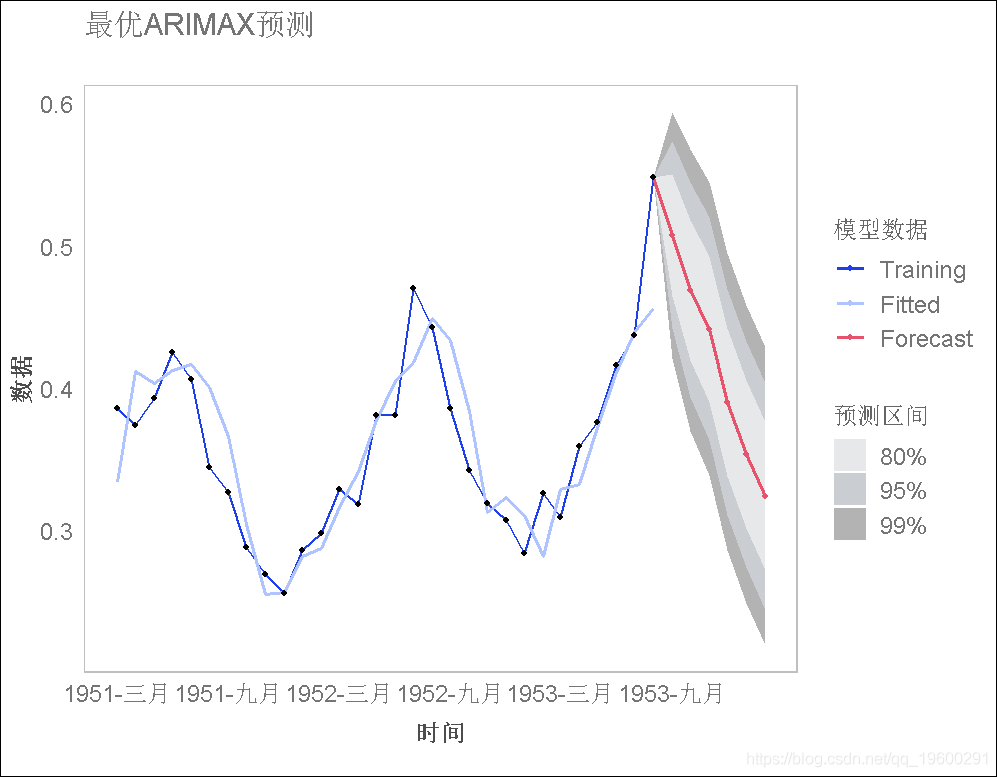
带有两个外部回归因子的模型具有最低的 平均绝对比例误差(0.528)
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python混合注意力机制-多变量-LSTM神经网络分析PM2.5、光伏电站、温度时间序列数据及RNN、ARIMAX、XGT、随机森林对比
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
R语言股价跳跃点识别：隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析
