如何用R语言在机器学习中建立集成模型？

By 大数据部落, 数理统计, 机器学习, 计算机科学与技术, ,

在本文中，我将向您介绍集成建模的基础知识。 另外，向您提供有关集合建模的实践经验。

WeChat Tencent QQ email print

由Kaizong Ye，Coin Ge撰写

通常，集成是一种组合两种或多种类似或不同类型算法的技术，称为基础学习者。


这样做是为了建立一个更加健壮的系统，其中包含了所有基础学习者的预测。可以理解为多个交易者之间的会议室会议，以决定股票的价格是否会上涨。由于他们都对股票市场有不同的理解。因此，他们应该根据自己对市场的理解对股票价格做出各种预测。

可下载资源

     完整程序、数据和文档（word）

2.集合的类型

在进一步详细介绍之前，一些基本概念是：

  • 平均：它被定义为 在回归问题的情况下或在预测分类问题的概率时从模型中获取预测的平均值。 
  • 多数投票：它被 定义为 在预测分类问题的结果的同时，从多个模型预测中以最大投票/推荐进行预测。 
  • 加权平均值：在此，不同的权重应用于来自多个模型的预测，然后取平均值 。 
×

集成学习主要围绕两个核心问题：

  • 如何选取个体学习器？

  • 如何选择结合策略？

1. 集成学习之个体学习器

个体学习器（又称为“基学习器”）的选择有两种方式：

  • 集成中只包含同种类型的个体学习器，称为同质集成 。

  • 集成中包含不同类型的个体学习器，为异质集成 。

目前同质集成 的应用最广泛，而基学习器使用最多的模型是CART决策树和神经网络。

按照个体学习器之间是否存在依赖关系可以分为两类：

  • 个体学习器之间存在强依赖关系，一系列个体学习器基本必须串行生成，代表是boosting系列算法。

  • 个体学习器之间不存在强依赖关系 ，一系列个体学习器可以并行生成，代表是bagging系列算法。

1.1 boosting算法原理

Boosting算法的工作机制是：

（1）先从初始训练集训练出一个基学习器；

（2）再根据基学习器的表现对样本权重进行调整，增加基学习器误分类样本的权重（又称重采样）；

（3）基于调整后的样本分布来训练下一个基学习器；

（4）如此重复进行，直至基学习器数目达到事先指定的个数 [公式] ，将这 [公式] 个基学习器通过集合策略进行整合，得到最终的强学习器。

Boosting系列算法里最著名算法主要有AdaBoost算法和提升树(boosting tree)系列算法。提升树系列算法里面应用最广泛的是梯度提升树(Gradient Boosting Tree)。后面我们会讲到这些优秀的算法。

1.2. 集成学习之Bagging 算法原理


bagging算法的工作机制为：

（1）对训练集利用自助采样法进行[公式]次随机采样，每次采样得到 [公式] 个样本的采样集；

（2）对于这 [公式] 个采样集，我们可以分别独立的训练出 [公式] 个基学习器；

（3）再对这 [公式] 个基学习器通过集合策略来得到最终的强学习器。

值得注意的是这里的随机采样采用的是自助采样法（Bootstrap sampling），自助采样法是一种有放回的采样。即对于 [公式] 个样本的原始训练集，我们每次先随机采集一个样本放入采样集，接着把该样本放回，这样采集 [公式] 次，最终可以得到 [公式] 个样本的采样集，由于是随机采样，这样每次的采样集是和原始训练集不同的，和其他采样集也是不同的。

对于一个样本，它每次被采集到的概率是 [公式] 。不被采集到的概率为 [公式] 。如果[公式]次采样都没有被采集中的概率是 [公式] 。则 [公式] ，即当抽样的样本量足够大时，在bagging的每轮随机采样中，训练集中大约有36.8%的数据没有被采集中。对于这部分大约36.8%的没有被采样到的数据，我们常常称之为袋外数据（Out Of Bag, 简称OOB）。这些数据未参与训练集模型的拟合，可以用来检测模型的泛化能力。

bagging对于弱学习器最常用的一般也是决策树和神经网络。bagging的集合策略也比较简单，对于分类问题，通常使用相对多数投票法。对于回归问题，通常使用算术平均法。

2. 集成学习之结合策略

上面几节主要关注于学习器，下面就对集成学习之结合策略做一个总结。我们假定我得到的T个弱学习器是 [公式]

2.1 平均法

平均法通常用于回归问题。

最简单的平均是算术平均，即：
[公式]
也可以是每个个体学习器的加权平均，即 ：
[公式]
其中 [公式] 是个体学习器 [公式] 的权重， [公式] 。

2.2 投票法

对于分类问题通常使用投票法。

假设我们的预测类别是 [公式] ，对于任意一个预测样本 [公式] ，我们的 [公式] 个弱学习器的预测结果分别是 [公式] 。主要有以下三种：

  • 相对多数投票法：也就是少数服从多数，即预测结果中票数最高的分类类别。如果不止一个类别获得最高票，则随机选择一个作为最终类别。

  • 绝对多数投票法：即不光要求获得最高票，还要求票过半数。

  • 加权投票法：每个弱学习器的分类票数要乘以一个权重，最终将各个类别的加权票数求和，最大的值对应的类别为最终类别。

2.3 Stacking

平均法和投票法仅是对弱学习器的结果做简单的逻辑处理，而stacking是再加上一层权重学习器（Meta Learner），基学习器（Base learner）的结果作为该权重学习器的输入，得到最终结果。

其中基学习器（Base learner）称为初级学习器，用于结合的学习器（Meta Learner）称为次级学习器。对于测试集，我们首先用初级学习器预测一次，将其输入次级学习器预测，得到最终的预测结果。

一些主要使用的技术：

  1. Bagging： Bagging也称为bootstrap聚合。 

增强的一些例子是XGBoost，GBM，ADABOOST等。

  1. 堆叠：在堆叠多层机器时，学习模型彼此叠加，每个模型将其预测传递给上面层中的模型，顶层模型根据模型下面的模型输出做出决策。

3.集合的优点和缺点

3.1优点

  • 集成是一种经过验证的方法，可以提高模型的准确性，适用于大多数情况。
  •  集成使模型更加稳健和稳定，从而确保在大多数情况下测试用例具有良好的性能。
  • 您可以使用集成来捕获数据中的线性和简单以及非线性复杂关系。这可以通过使用两个不同的模型并形成两个集合来完成。

视频

Boosting集成学习原理与R语言提升回归树BRT预测短鳍鳗分布生态学实例

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

3.2缺点

  • 集成减少了模型的可解释性，并且很难在最后绘制任何关键的业务见解。
  • 这非常耗时，因此可能不是实时应用程序的最佳选择。

4.在R中实施集合的实用指南

 
＃让我们看一下数据集数据的结构
 'data.frame'：614 obs。13个变量：
  
$ ApplicantIncome：int 5849 4583 3000 2583 6000 5417 2333 3036 4006 12841 ...
$ CoapplicantIncome：num 0 1508 0 2358 0 ...
$ LoanAmount：int NA 128 66 120 141 267 95 158 168 349 ...
$ Loan_Amount_Term：int 360 360 360 360 360 360 360 360 360 360 ...
$ Credit_History：int 1 1 1 1 1 1 1 0 1 1 ...
 
 
＃使用中位数填充缺失值
preProcValues < -  preProcess（data，method = c（“medianImpute”，“center”，“scale”））
 

#Spliting训练根据结果分为两部分：75％和25％
index < -  createDataPartition（data_processed $ Loan_Status，p = 0.75，list = FALSE）
trainSet < -  data_processed [index，]
testSet < -  data_processed [-index，]

我将数据分成两部分，我将用它来模拟训练和测试操作。我们现在定义训练以及预测变量和结果变量：

＃定义多个模型的训练参数
fitControl < -  trainControl（
  method =“cv”， savePredictions ='final'，
classProbs = T）

我们开始训练随机​​森林并在我们创建的测试集上测试其准确性：

 
＃检查随机森林模型的准确性 
Confusion matrix and statistics
reference
Forecast N Y.
N 28 20
Y 9 96
Accuracy: 0.8105
95% CI: (0.7393,0.8692)
No information rate: 0.7582
P value[Acc> NIR]: 0.07566
Kappa: 0.5306
Mcnemar's test P value: 0.06332
Sensitivity: 0.7568
Specificity: 0.8276
Pos Pred value: 0.5833
Neg Pred value: 0.9143
Prevalence rate: 0.2418
Detection rate: 0.1830
Detection prevalence rate: 0.3137
Balance accuracy: 0.7922

 我们使用随机森林模型获得了0.81的准确度。让我们看看KNN的表现：

最受欢迎的见解

1.从决策树模型看员工为什么离职

2.R语言基于树的方法：决策树，随机森林

3.python中使用scikit-learn和pandas决策树

4.机器学习：在SAS中运行随机森林数据分析报告

5.R语言用随机森林和文本挖掘提高航空公司客户满意度

6.机器学习助推快时尚精准销售时间序列

7.用机器学习识别不断变化的股市状况——隐马尔可夫模型的应用

8.python机器学习：推荐系统实现（以矩阵分解来协同过滤）

9.python中用pytorch机器学习分类预测银行客户流失

＃训练knn模型 
#使用knn模型预测
testSet $ pred_knn <-predict（object = model_knn，testSet [，predictors]）
＃检查随机森林模型的准确性 
reference
Forecast N Y.
N 29 19
Yes 2 103
Accuracy: 0.8627
95% CI: (0.7979, 0.913)
No information rate: 0.7974
P value[Acc> NIR]: 0.0241694
Kappa: 0.6473
Mcnemar's test P value: 0.0004803
Sensitivity: 0.9355
Specificity: 0.8443
Pos Pred value: 0.6042
Neg Pred value: 0.9810
Prevalence rate: 0.2026
Detection rate: 0.1895
Detection prevalence rate: 0.3137
Balance accuracy: 0.8899

R语言基于树的方法：决策树，随机森林，Bagging，增强树

阅读文章 ➜

 我们能够通过单独的KNN模型获得0.86的准确度。Logistic回归的表现：

#训练Logistic回归模型 
#预测使用knn模型
testSet $ pred_lr <-predict（object = model_lr，testSet [，predictors]）
＃检查随机森林模型的准确性 
Confusion matrix and statistics
reference
Forecast N Y.
N 29 19
Yes 2 103
Accuracy: 0.8627
95% CI: (0.7979, 0.913)
No information rate: 0.7974
P value[Acc> NIR]: 0.0241694
Kappa: 0.6473
Mcnemar's test P value: 0.0004803
Sensitivity: 0.9355
Specificity: 0.8443
Pos Pred value: 0.6042
Neg Pred value: 0.9810
Prevalence rate: 0.2026
Detection rate: 0.1895
Detection prevalence rate: 0.3137
Balance accuracy: 0.8899

逻辑回归也给出了0.86的准确度。

现在，让我们尝试用这些模型形成集合的不同方法，如我们所讨论的：

平均

我们将平均三个模型的预测。由于预测是“Y”或“N”，因此平均值对于此二进制分类没有多大意义。但是，我们可以对观察概率的平均值进行平均处理。

随时关注您喜欢的主题

#预测概率
testSet $ pred_rf_​​prob <-predict（object = model_rf，testSet [，predictors]，type ='prob'）
testSet $ pred_knn_prob <-predict（object = model_knn，testSet [，predictors]，type ='prob'）
testSet $ pred_lr_prob <-predict（object = model_lr，testSet [，predictors]，type ='prob'）

多数表决：在多数表决中，我们将为大多数模型预测的观察指定预测。

多数投票加权平均值

我们可以采用加权平均值，而不是采用简单平均值。通常，对于更准确的模型，预测的权重很高。让我们将0.5分配给logistic回归，将0.25分配给KNN和随机森林。 

到目前为止，我们在顶层使用了简单的公式。相反，我们可以使用另一种机器学习模型，这就是堆叠。我们可以使用线性回归来制作线性公式，用于在回归问题中进行预测，以便在分类问题的情况下将底层模型预测映射到结果或逻辑回归。

在同一个例子中，让我们尝试将逻辑回归和GBM应用为顶层模型。请记住，我们将采取以下步骤：

  1. 在训练数据上训练各个基础层模型。
  2. 预测使用每个基础层模型来训练数据和测试数据。
  3. 现在，再次对顶层模型进行训练，对底层模型进行训练数据的预测。
  4. 最后，使用顶层模型预测底层模型的预测。

首先，让我们从GBM模型开始作为顶层模型。

  • 步骤1：在训练数据上训练各个基础层模型
#定义参数
fitControl < -  trainControl（
method =“cv”， savePredictions ='final'，＃保存最佳参数组合的预测
classProbs = T＃保存预测的类概率
）
#训练随机森林模型
＃训练knn模型 
#训练逻辑回归模型  
  • 步骤2：使用每个基础层模型预测训练数据和测试数据
#预测训练数据的概率 
#预测测试数据的概率
  • 步骤3：现在再次训练顶层模型对底层模型的预测已经对训练数据进行了预测

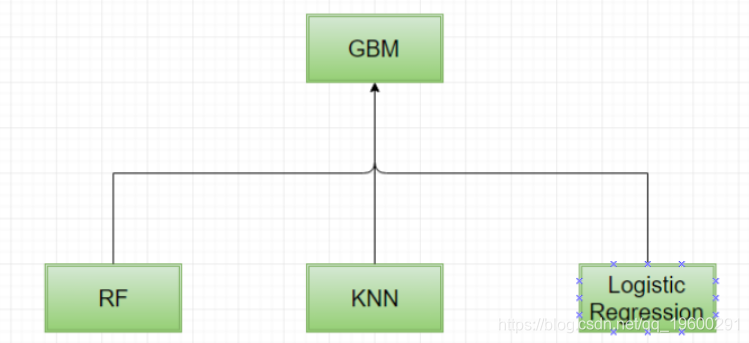
#顶层模型用于预测的变量
predictors_top <-c（ 'OOF_pred_rf'， 'OOF_pred_knn'， 'OOF_pred_lr'） 
#GBM作为顶层模型

同样，我们也可以使用逻辑回归创建一个集合作为顶层模型。

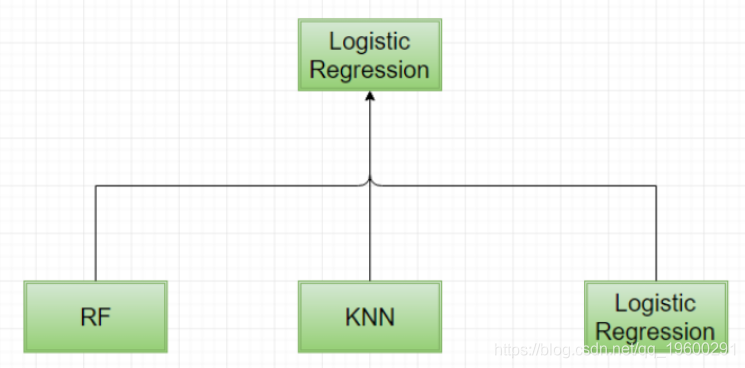
#Logistic回归作为顶层模型
model_glm < - 
 （ [，predictors_top]，  trControl = fitControl，tuneLength = 3）
  • 步骤4：最后，使用顶层模型预测
#使用GBM顶层模型预测
测试集$ gbm_stacked <-predict（model_gbm，测试集[，predictors_top]）
#使用logictic回归顶层模型预测
测试集$ glm_stacked <-predict（model_glm，测试集[，predictors_top]）

注意， 选择模型非常重要，以便从整体中获得最佳效果。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

​非常感谢您阅读本文，如需帮助请联系我们！

 
QQ在线咨询
售前咨询热线
15121130882
售后咨询热线
0571-63341498
微信扫一扫
关注拓端助手

关注有关新文章的微信公众号

永远不要错过任何见解。当新文章发表时，我们会通过微信公众号向您推送。

技术干货

最新洞察

This will close in 0 seconds