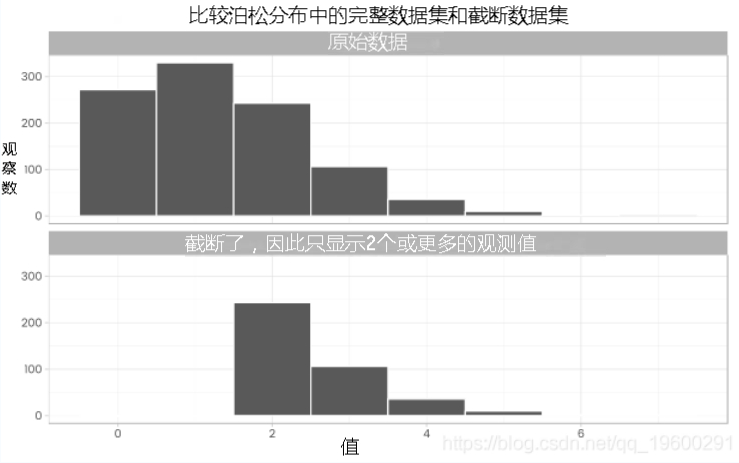
这是一个非常简化的例子。我模拟了1,000个计数观察值，平均值为1.3。
然后，如果只观察到两个或更高的观察，我将原始分布与我得到的分布进行比较。
可下载资源
由此代码生成：
# 原始数据：
set.seed(321)
a <- rpois(1000, 1.3)
# 数据的截断版本：
b <- a[ a > 1]
# 图形：
data_frame(value = c(a, b),
ggplot(aes(x = value)) +
(binwidth = 1, colour = "w
# 模型拟合原始模型效果很好：
mean(a)
(a, "Poisson")
# 截断版本效果一般
mean(b)
fitdistr(b, "Poisson")估计lambda完整数据（a）的关键参数效果很好，估计值为1.347，刚好超过1.3的真实值的一个标准误差。
最大似然
估计lambda完整数据（a）的关键参数效果很好，估计值为1.347，刚好超过1.3的真实值的一个标准误差。
最大似然
在fitdist中使用dpois和ppois函数的截断版本。
#-------------在R中使用MLE拟合-------------------
dtruncated_poisson <- function(x, lambda) {
}
ptruncated_poisson <- function(x, lambda) {
}
fitdist(b, "truncated_poisson", start = c(lambda = 0.5)) 视频
R语言中RStan贝叶斯层次模型分析示例
请注意，要执行此操作，我将下限阈值指定为1.5; 因为所有数据都是整数，这实际上意味着我们只观察2或更多的观察结果。我们还需要为估计值指定一个合理的起始值lambda，不让误差太大。
贝叶斯
对于替代贝叶斯方法，Stan可以很容易地将数据和概率分布描述为截断的。除了我x在这个程序中调用的原始数据之外，我们需要告诉它有多少观察（n），lower_limit截断，以及表征我们估计的参数的先验分布所需的任何变量。
以下程序的关键部分是：
- 在
data中，指定数据的x下界为lower_limit - 在
model中，指定x通过截断的分布T[lower_limit, ]
data {
int n;
int lower_limit;
int x[n];
real lambda_start_mu;
real lambda_start_sigma;
}
parameters {
reallambda;
}
model {
lambda ~ normal(lambda_start_mu, lambda_start_sigma);
for(i in 1:n){
x[i] ~ poisson(lambda) T[lower_limit, ];
}
}以下是从R向Stan提供数据的方式：
#-------------从R中调用Stan--------------
data <- list(
x = b,
lower_limit = 2,
n = length(),
lambda_start_sigma = 1
)
fit <- stan("0120-trunc.stan", data = data, cores = 4)
plot(fit) +
labs(y = "Estimated parameters") +
theme_minimal(base_family = "myfont")结果提供了lambda与fitdistrplus方法估计的后验分布：1.35，标准偏差为0.08。置信区间的图像：
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言宏观经济学：IS-LM曲线可视化货币市场均衡
