使用线性模型、回归决策树自动组合特征因子水平

---

可下载资源

因此我想编写一个R函数。为了说明这一点，请考虑以下内容

'data.frame':	200 obs. of  3 variables:
 $ y : num  1.345 1.863 1.946 2.481 0.765 ...
 $ x1: num  0.266 0.372 0.573 0.908 0.202 ...
 $ x2: Factor w/ 10 levels "I","A","H","F",..: 4 4 6 4 3 6 7 3 4 8 ...
table(b$x2)[LETTERS[1:10]]
 
 A  B  C  D  E  F  G  H  I  J 
11 12 23 34 23 36 12 32  3 14

没有定义一个（连续的）因变量，没有定义一个连续的协变量，也没有定义一个分类变量，此处有十个级别。我们可以使用

---

视频

从决策树到随机森林：R语言信用卡违约分析信贷数据实例

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

plot(b$x1,y,col="white",xlim=c(0,1.1))
text(b$x1,y,as.character(b$x2),cex=.5)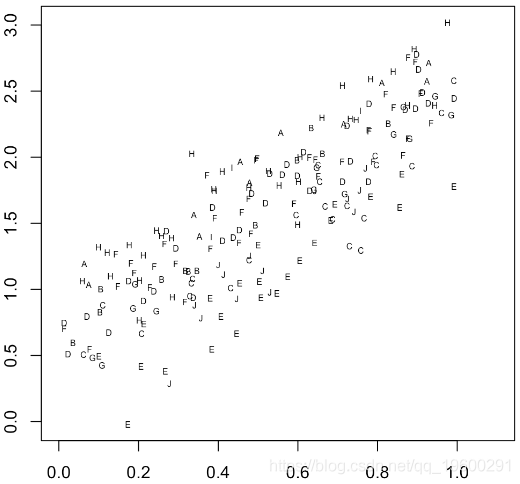

​

线性回归的输出得出以下预测

for(i in 1:10){



lines(u,v)}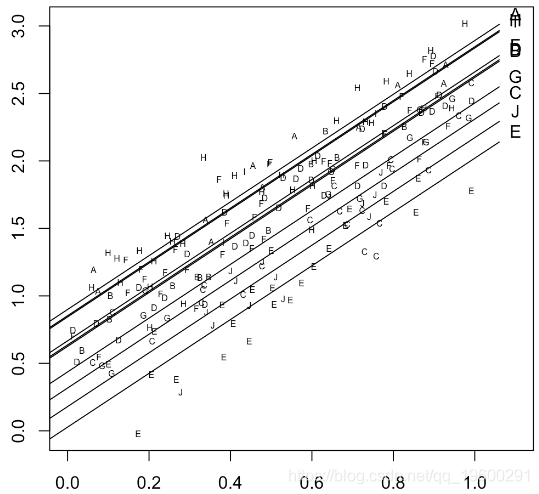

​

斜率是相同的，我们只需为每个级别添加一个不同的常数。如我们所见，某些级别非常接近，因此将它们组合为一个类别。这是线性回归的输出，

plot(1:nlevels(b$x2),1:nlevels(b$x2),col="white",xlab="",ylab="",axes=F,xlim=c(0,10.5),
     ylim=c(0,10.5))





points(((1:10))[idx],rep(i,length(idx)),pch=1,cex=2)

points(((1:10))[idx],rep(i,length(idx)),pch=19,cex=2)}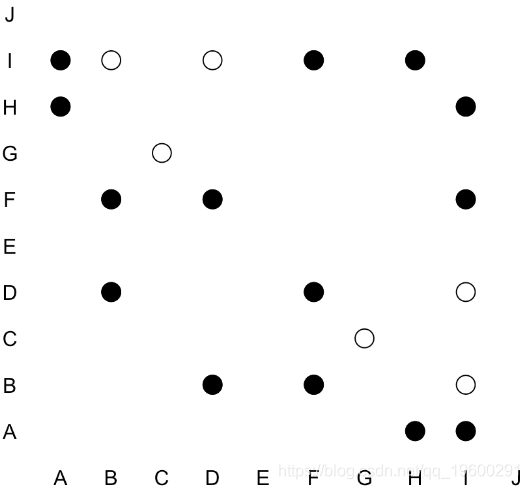

​

我们看到它是对称的：如果将“ H”与“ I”组合，则“ I”也应与“ H”组合。

我们可以手动预定义一些顺序

for(i in 1:nlevels(b$x2)){





  points(((1:10))[idx],rep(i,length(idx)),pch=1,cex=2)
  idx=which(p>.1)
  points(((1:10))[idx],rep(i,length(idx)),pch=19,cex=2)
}

我们得到

​

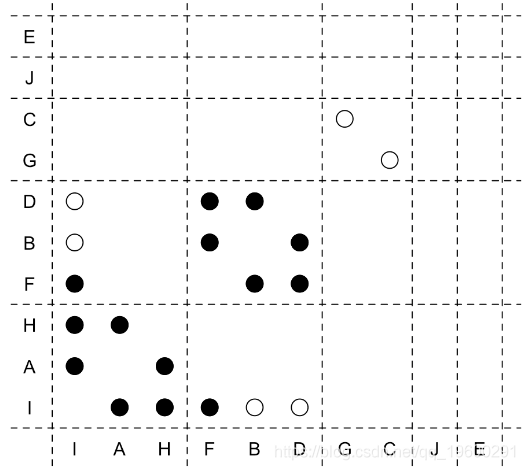
我们已经合并了类别。

实际上，可以使用其他策略。我们从某个级别开始，说“ A”。然后，我们将其与所有不显着不同的级别合并。如果“ B”不是其中之一，我们将其用作新参考。

for(i in 1:nlevels(b$x2)){
 





  b$x2=recode(b$x2, paste("c('",paste(mix,collapse = "','"),"')='",paste(mix,collapse = "+"),"'",sep=""))
}}

最后的类别是

table(b$x2)
 
A+I+H B+D+F   C+G     E     J 
   46    82    35    23    14

有以下回归输出

 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.86407    0.03950  21.877  < 2e-16 ***
x1           1.99180    0.05323  37.417  < 2e-16 ***
x2B+D+F     -0.21517    0.03699  -5.817 2.44e-08 ***
x2C+G       -0.50545    0.04528 -11.164  < 2e-16 ***
x2E         -0.83617    0.05128 -16.305  < 2e-16 ***
x2J         -0.68398    0.06131 -11.156  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 0.2008 on 194 degrees of freedom
Multiple R-squared:  0.8975,	Adjusted R-squared:  0.8948 
F-statistic: 339.6 on 5 and 194 DF,  p-value: < 2.2e-16

AIC
[1] -66.76939
BIC
[1] -43.68117

这与我们之前得到的组一致。但是，如果我们更改顺序，我们可以得到不同的组合。例如，如果我们从“ J”到“ A”，而不是从“ A”到“ J”，我们得到

for(i in nlevels(b$x2):1){





  mix=c(LETTERS[i],names(p)[idx])
  b$x2=recode(b$x2, paste("c('",paste(mix,collapse = "','"),"')='",paste(mix,collapse = "+"),"'",sep=""))
}}
table(b$x2)
 
          E         G+C I+A+B+D+F+H           J 
         23          35         128          14

这里有不同的信息标准

AIC(lm(y~x1+x2,data=b))
[1] -36.61665
BIC(lm(y~x1+x2,data=b))
[1] -16.82675

最后但重要的一点是，可以使用回归树。问题是还有另一个可能相互干扰的解释变量。所以我建议（1）拟合线性模型，计算残差（2）运行回归树，解释未定义分类变量

​

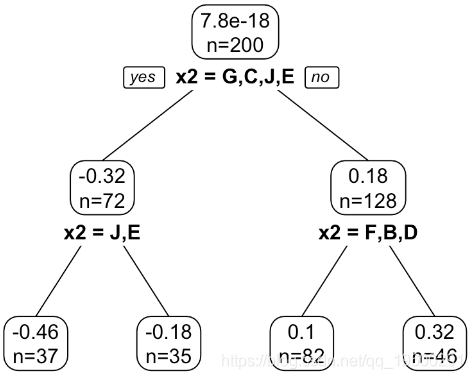
观察叶子与我们得到的叶子具有相同的组。

arbre
n= 200 
 
node), split, n, deviance, yval
      * denotes terminal node
 
1) root 200 22.563500  7.771561e-18  
  2) x2=G,C,J,E 72  4.441495 -3.232525e-01  
    4) x2=J,E 37  1.553520 -4.578492e-01 *
    5) x2=G,C 35  1.509068 -1.809646e-01 *
  3) x2=I,A,H,F,B,D 128  6.366628  1.818295e-01  
    6) x2=F,B,D 82  2.983381  1.048246e-01 *
    7) x2=I,A,H 46  2.030229  3.190993e-01 *

我想有可能改善回归的水平组合。