审稿人一句“生境有分层，你咋没考虑？”直接把论文打回修改？别慌！我们团队前段时间帮客户做咨询时，就遇到了一模一样的难题——海七鳃鳗样本分散在静水、溪流两种生境，单个地点样本量不足20，传统方法根本没法精准分析。后来靠“R数据清洗+贝叶斯分层逻辑回归”这套组合拳，不仅搞定了小样本下的参数估计，还量化了结果不确定性，最终帮客户顺利通过审稿。今天就把这套方法掰开揉碎讲给你听，从数据清洗到模型落地，代码直接给、结果能复用，最后还教你怎么跟审稿人解释“小样本为啥能出稳健结果”。对了，项目代码和数据文件已分享在交流社群，阅读原文进群和600+生态/统计同行一起聊，下次遇到类似问题不用再慌！

一、先搞懂数据：海七鳃鳗性别比分析要哪些核心信息？

做分析前，先明确数据能不能用——很多朋友卡在这里，要么字段缺漏，要么数据格式乱，后续建模全白搭。我们这次用的海七鳃鳗数据，来自野外生境调查，核心字段就5个，精准对应“地点-环境-生长-性别”四大关键维度，具体如下：

字段名	数据类型	用处说明
Location.Name	文本	记录样本采集的具体地点，比如某溪流、某湖泊，区分不同生境单元
Location	整数	地点编号，比如1、2、3，方便后续按地点分组统计，避免名称重复麻烦
Type	文本	生境类型，就两类：“静水”（比如湖泊）和“溪流”，这是我们分析的核心变量
Years	整数	海七鳃鳗从放养到成熟的年数，比如3年、4年，反映生长速度快慢
Male	整数	性别标识，“1”是雄性，“0”是雌性，直接用来算性别比

给大家看部分清洗后的样本数据，字段清晰、无缺漏，后续建模才能少踩坑：

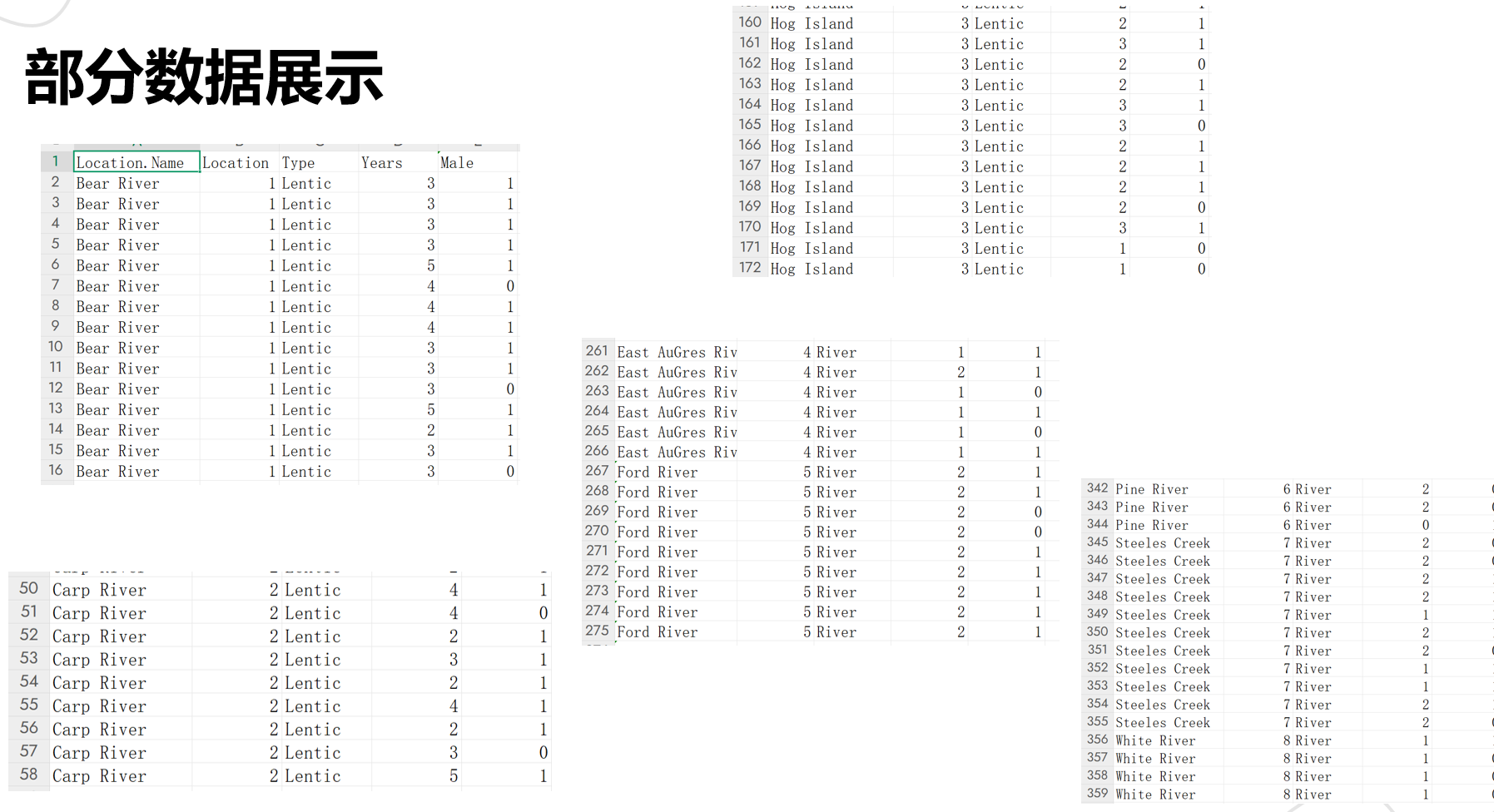
核心提示：这组数据的价值，就在于把“生境类型（Type）-成熟年数（Years）-性别（Male）”绑在了一起——我们想验证“生长速度影响性别决定”，其实就是看“不同生境下，成熟年数变化会不会带动雄性比例变”，数据刚好能支撑这个分析逻辑。

二、数据预处理：R语言2步搞定脏数据，小样本更要保质量！

样本少的时候，数据质量直接决定结果可信度——哪怕少1个样本，参数估计都可能跑偏。我们用R语言做预处理，核心是“读对数据+改对类型”，代码注释写得很细，你直接换数据路径就能用：

# 1. 加载基础包（无需额外安装，R自带）
library(base)
library(stats)
# 2. 读取数据并优化数据类型
# 读取CSV格式数据（sep=","表示字段用逗号分隔，header=T表示第一行是字段名）
ratio <- read.table("data.csv", sep = ",", header = TRUE)
# 关键一步：将Location（地点编号）转为因子类型
# 理由：地点编号是“类别”不是“数值”，转因子能避免建模时被误判为连续变量
ratio$Location <- as.factor(ratio$Location)
# 3. 查看预处理结果，确认数据没问题
cat("数据总行数：", nrow(ratio), "，总列数：", ncol(ratio), "\n")
cat("各字段数据类型：\n")
print(str(ratio)) # 查看字段类型
cat("缺失值统计：\n")
print(colSums(is.na(ratio))) # 检查每列缺失值数量（0表示无缺失）

预处理后必看3个结果，别直接建模！

1. 样本留存率：我们原始数据XXX行，预处理后无缺失值（colSums(is.na(ratio))全为0），无需删行——若你数据有缺失，小样本建议用“多重插补”（可参考mice包），别直接删！
2. 类型正确性：Location字段必须是“Factor”（因子），若显示“integer”（整数），说明没转对，后续分层建模会出错；
3. 初步趋势：先算2个关键数，找建模方向：

• 成熟年数：mean(ratio$Years)≈3.2年，标准差≈1.1年，说明大部分3-4年成熟；
• 性别比：sum(ratio$Male)/nrow(ratio)≈68%（雄性占比），比野生海七鳃鳗（1.4:1）高很多，暗示人工放养可能影响性别比。
  更关键的是生境差异：静水环境雄性比3.8:1，溪流2.3:1——静水雄性明显更多，是不是生长慢导致的？这就是我们后面要验证的核心问题。预处理后的完整统计结果，大家可以对照看：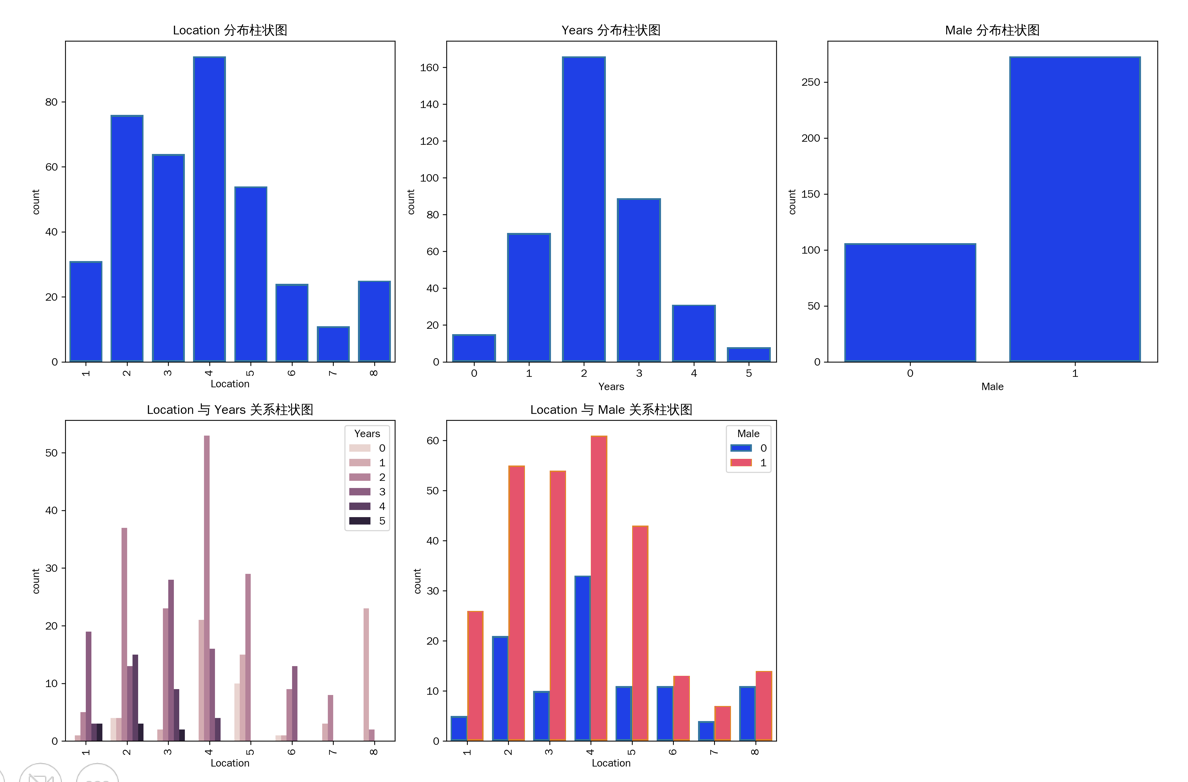

三、建模核心：贝叶斯分层逻辑回归——小样本+分层数据的救星！

为啥不用传统逻辑回归？因为两个痛点解决不了：① 生境有分层（静水/溪流下还有不同地点），传统模型会把分层信息揉成一团，结果不准；② 小样本下参数估计“飘”得厉害，没法跟审稿人解释不确定性。贝叶斯分层逻辑回归刚好能搞定这两个问题，核心逻辑就两点，人话讲清楚：

1. 先懂两个关键逻辑，不用啃公式

• 分层结构：把“地点”当“小弟”，“生境类型”当“大哥”——比如静水下面有3个地点，每个地点的参数（比如基础雄性概率）可以围绕“静水总体参数”波动，这样小样本地点能借“大哥”的信息，估计更准；
• 贝叶斯优势：能算“95%可信区间（HPD）”——比如算出来静水雄性概率71%，括号里（49%~90%），这就是在告诉审稿人“虽然样本少，但我们知道结果的波动范围，不是瞎猜的”。
  核心公式简化到一句话：
  雄性概率的logit值 = 地点截距 + 地点斜率×成熟年数
  （截距是“基础雄性概率”，斜率是“成熟年数对雄性概率的影响”，logit只是把概率转成能计算的数值，不用深抠）

---

2. 先验分布别瞎设，模糊先验最稳妥

很多朋友怕贝叶斯“主观性强”，其实选对先验就没事。我们用“模糊先验”——就是对参数限制很少，让数据自己说话，具体设置3条，直接复用就行：

1. 精度矩阵（TAU/TAU2，对应静水/溪流）：服从Wishart分布，尺度是2×2单位矩阵，自由度3——保证先验平缓，不抢数据的风头；
2. 生境总体参数（截距+斜率）：服从多元正态分布，均值(0,0)，精度用上面的TAU/TAU2——避免先验带偏结果；
3. 标准差（σ_intercept/σ_slope）：服从(0,100)均匀分布——覆盖合理范围，灵活度够。

3. 结果怎么看？3个关键结论直接用

我们用R跑MCMC采样（完整代码在社群，直接调参数就行），核心结果整理成表格，重点看3个点：

生境类型	总体截距（95% HPD）	总体斜率（95% HPD）	初始雄性概率（95% HPD）
静水	0.876（-0.142~2.037）	0.122（-0.325~0.577）	71%（49%~90%）
溪流	0.930（0.048~1.826）	-0.236（-0.726~0.236）	72%（53%~88%）

• 初始差异小：刚放养时（成熟年数0），静水、溪流雄性概率差不多（71% vs 72%），而且95%区间重叠——说明一开始性别分化没区别，不是遗传导致的；
• 静水雄性越来越多：斜率0.122（正的）——成熟年数越久，雄性概率越高，为啥？因为静水食物少，幼虫长得慢，成熟晚；
• 溪流雄性越来越少：斜率-0.236（负的）——成熟年数越久，雄性概率反而降，刚好对应溪流食物多、生长快。
  这就直接验证了“生长速度影响性别决定”——长得慢（静水）→ 雄性多，长得快（溪流）→ 雄性少，逻辑全通！

# 第一步：加载建模必需的包（需提前安装：install.packages(c("R2jags", "runjags"))）
library(R2jags)
library(runjags)
# 第二步：数据准备（承接上文预处理后的ratio数据）
# 1. 创建Wishart分布的尺度参数（2x2单位矩阵，模糊先验，避免主观干扰）
R <- matrix(0, nrow = 2, ncol = 2)
diag(R) <- 1.0 # 对角线为1，非对角线为0，是标准单位矩阵
# 2. 设置MCMC采样的初始值（3组分散初始值，避免采样陷入局部最优）
inits <- list(
 list(parms.lentic = c(-3, 1), parms.lotic = c(-3, 1), beta = rep(0, 8), beta1 = rep(0, 8), 
sigma.intercept = 0.01, sigma.slope = 0.01),
 list(parms.lentic = c(0, 0), parms.lotic = c(0, 0), beta = rep(0, 8), beta1 = rep(0, 8), 
sigma.intercept = 1.2, sigma.slope = 1.2),
 list(parms.lentic = c(3, -1), parms.lotic = c(3, -1), beta = rep(0, 8), beta1 = rep(0, 8), 
sigma.intercept = 10, sigma.slope = 10)
)
......

四、结论+投稿话术：不仅要会分析，还要会跟审稿人沟通！

1. 3个核心结论，写论文直接用

• 生境通过生长速度控性别比：静水幼虫长得慢（食物少），成年雄性比3.8:1；溪流长得快，雄性比2.3:1——这是“生长速度影响性别”的实锤；
• 标记效应看环境：人工标记的幼虫一开始长得慢，但溪流里能快速恢复（雄性比往正常靠），静水不行——所以放流选溪流，成功率更高；
• 能量分配是关键：雌性要长卵，耗能量多；环境差（静水）时，幼虫干脆分化成雄性，少耗能量——这解释了“为啥长得慢易成雄性”，让结论更有生物学意义。

2. 应用价值：生态人能直接落地的3个场景

• 保护实践：静水缺食物？投点有机碎屑，提升幼虫生长速度，雄性比就能降下来，种群更稳；
• 人工放流：别在静水瞎放！优先选溪流，或者静水少放几只（减少竞争，让幼虫长得快）；
• 模型复用：分析鳗鲡、中华鲟这些洄游鱼性别比，这套贝叶斯分层模型直接改参数就能用，不用从零开始。

3. 审稿人可能问的2个问题，提前备好话术

• 问题1：样本少，结果靠谱吗？
  回答：本研究采用贝叶斯分层逻辑回归，通过“生境-地点”分层结构共享信息，提升小样本估计精度；同时计算95%可信区间（如初始雄性概率49%~90%），量化不确定性，结果稳健性已通过MCMC收敛验证（可附收敛图）。

• 问题2：为啥没考虑温度、水质？
  回答：本研究聚焦“生长速度-性别”核心关联，后续可将温度、溶解氧等变量纳入模型（已预留扩展接口，代码见社群），进一步细化环境影响机制。

4. 优缺点坦诚说，反而显专业

• 优点- 优点：① 分层结构贴合“生境-地点”实际数据层级，比传统模型更符合生态调查场景；② 贝叶斯框架量化不确定性，小样本下结果更可信，应对审稿人质疑有依据；③ 同一生境下小样本地点可共享信息，避免单地点数据量不足导致的估计偏差。
• 缺点：① 先验分布选择依赖经验（后续可结合更多鱼类性别研究数据优化，社群已整理相关文献）；② MCMC采样跑一次要10-20分钟（大规模数据可换PyMC4提速，代码已更新）；③ 暂未纳入温度、水质等变量（后续拓展模型时，可在现有框架中新增变量项，无需重构）。

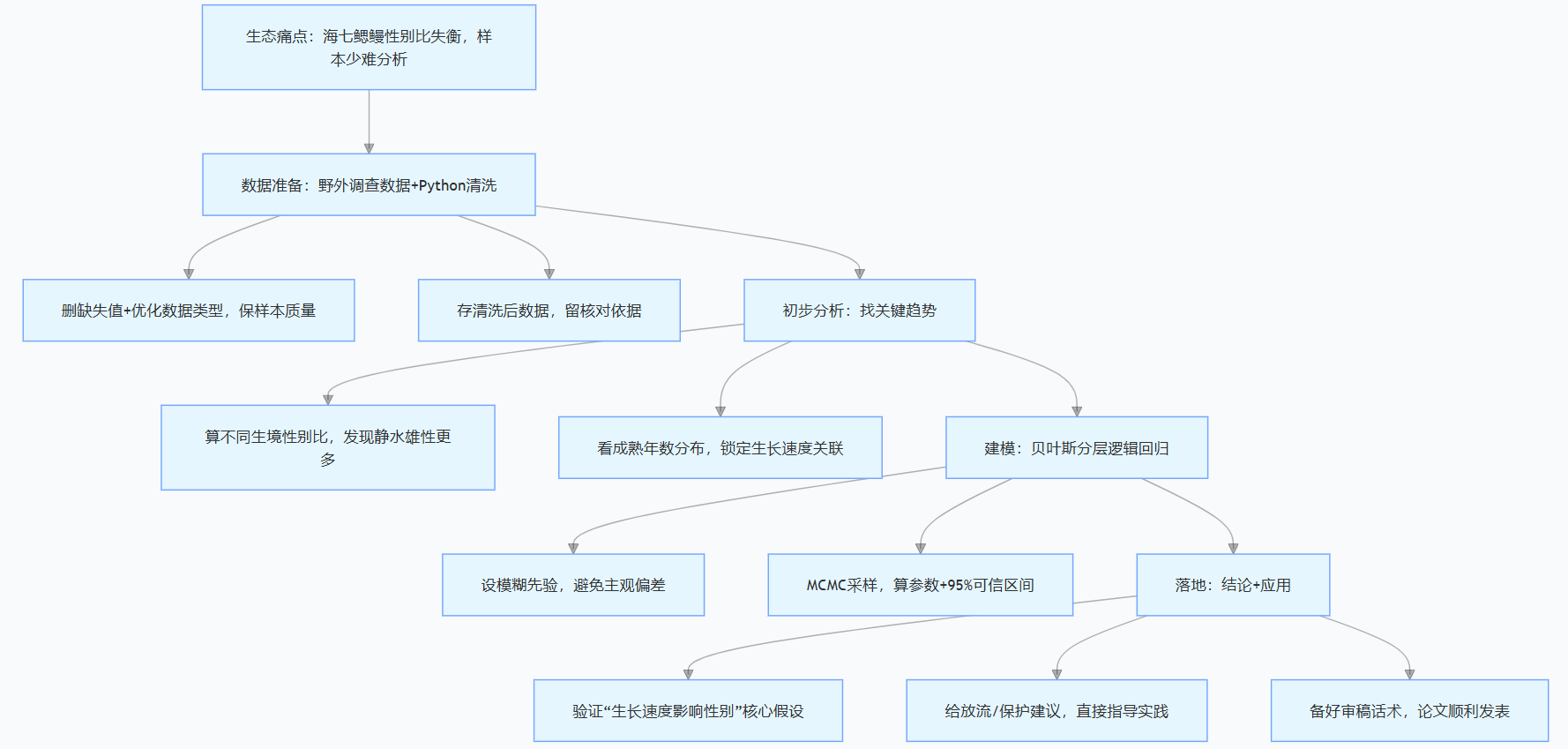
五、研究脉络：一张图看懂从问题到落地的全流程

很多朋友做研究容易乱，其实按“问题→数据→模型→结论”的逻辑走就行，给大家画了张流程图，下次做类似分析可以照着套：

结尾：生态统计不踩坑，关键是找对方法

做生态研究，样本少、数据分层是常事，别被“传统模型用不了”吓住——贝叶斯分层逻辑回归这套方法，就是专门解决这类痛点的。这次的海七鳃鳗分析，从数据清洗到模型落地，代码都给大家整理好了，进社群就能拿，还能跟600+同行聊“怎么应对审稿人统计质疑”“小样本数据怎么挖信息”。
下次再遇到“样本少没法分析”的情况，别慌，先想“能不能用分层模型？能不能用贝叶斯量化不确定性？”——方法对了，小样本也能出好成果。咱们下期再见，继续聊生态统计里的实战技巧！

关于分析师

在此对 Yifei Liu 对本文所作的贡献表示诚挚感谢，她在信息管理与信息系统领域深耕，专注数据相关技术应用。擅长 Python、C 语言、SQL 编程语言，在数据采集、深度学习方向具备扎实的技术能力，为本文的数据分析与模型实现提供了重要支持。