最近我们被客户要求撰写关于MCMC采样的研究报告。在许多情况下,我们没有足够的计算能力评估空间中所有n维像素的后验概率 。在这些情况下,我们倾向于利用称为Markov-Chain Monte Carlo 算法的程序 。
此方法使用参数空间中的随机跳跃来(最终)确定后验分布。MCMC的关键如下:
跳跃概率的比例与后验概率的比例成正比。
跳跃概率可以表征为:
概率(跳跃)*概率(接受)
从长远来看,该链将花费大量时间在参数空间的高概率部分,从而实质上捕获了后验分布。有了足够的跳跃,长期分布将与联合后验概率分布匹配。
可下载资源
MCMC本质上是一种特殊类型的随机数生成器,旨在从难以描述(例如,多元,分层)的概率分布中采样。在许多/大多数情况下,后验分布是很难描述的概率分布。
1.1 基本概念
-
从一个概率分布(目标分布
)中得到随机样本序列
-
这个序列可以用于:a) 近似估计分布
; b) 计算积分(期望)
-
用于高维分布取样
-
缺陷: MCMC固有缺点, 样本自相关性
1.2 优势
-
可以从任意的概率分布
中取样,只要满足条件:函数
成比例于
的密度。
-
更宽松的要求:
仅需要与
的密度成比例。
1.3 要点
-
生成样本值序列;样本值产生得越多,这些值的分布就越近似于
-
迭代产生样本值:下一个样本的分布仅仅取决于当前样本值(马尔科夫链特性)
-
接受/拒绝概率:接受计算出的值为下一个样本值/拒绝并重复使用当前样本值;基于
,接受概率通过比较
(当前值)和
(备选值)得出
1.4 Metropolis Algorithm (对称分布)
-
Input:
,与目标分布
成比例的函数
1. 初始化:
-
: 取任意点作为第一个样本值
-
: 任意的概率密度函数;给定上一个样本值
,计算出下一个样本值
; 一般我们设定
是对称的,即
;我们也会令
服从以
为中心的
分布,即越靠近
,概率越大
-
将样本序列制成随机游走(random walk);
: 假定密度/跳跃分布(jumping distribution)
2. 迭代
-
通过密度函数
生成备选样本值
-
计算接受备选样本值的比率:
;由于
又与
成比例,因此
。
-
若
,
比
更接近
,令
;否则,以
的概率接受备选样本值
;若备选样本值被拒绝,令
。
1.5 缺陷
-
样本自相关:相邻的样本会相互相关,虽然可以通过每
步取样的方式来减少相关性,但这样的后果就是很难让样本近似于目标分布
。
-
自相关性可通过增加步调长度(jumping width,与jumping function
的方差有关)来控制,但同时也增加了拒绝备选样本的几率
。
-
过大或过小的jumping size会导致slow-mixing Markov Chain, 即高度自相关的一组样本,以至于我们需要得到非常大的样本量
才能得到目标分布
。
-
初始值的选择:尽管Markov Chain最后都会收敛到目标分布,然而初始值的选择直接影响到运算时间,尤其是把初始值选在在了“低密度”区域。因此,选择初值时,最好加入一个“burn-in period”(预烧期,预选期)。
1.6 优势
-
抗“高维魔咒”(curse of dimensionality):维度增加,对于rejection sampling方法来说,拒绝的概率就是呈指数增长。而MCMC则成为了解决这种问题的唯一方法
-
多元分布中,为了避免多元初始值以及
选择不当而导致的问题,Gibbs sampling是另外一个更适合解决多元分布问题的MCMC 方法。Gibbs sampling从多元分布的各个维度中分别选择初始值,然后这些变量分别同时取样。
1.7 衍生算法
Metropolis-Hastings算法的目的是根据目标分布生成一个状态集。算法运用了渐进于平稳分布
的Markov过程使得
。
Markov过程由它的状态转换概率所决定的。为从任意状态
转化到另外一个任意状态
的转换概率。当它符合以下两点是,它有唯一的平稳分布
:
-
平稳分布
的存在性:充分但非必要条件为细致平衡(detailed balance):每一个转换
都是可逆的,即对任意连个状态
和
,在状态
时
的概率等于在状态
时
的概率,即
-
平稳分布
的唯一性:由Markov过程的遍历性可得,即每一个转换
需满足:
-
非周期性的(aperiodic):系统不会再某一个固定时间区间内回到原状态
-
正递归的(positive recurrent):回到同一个状态的步数的期望是有限值
Metropolis-Hastings算法需要通过构建转换概率来构建一个Markov过程且需要满足以上两点来使得Markov过程的平稳分布就是目标分布
。算法衍生从满足细致平衡条件开始:
,
即 (1)
这样就把转换的细致平衡转化为两步:提议和接受-拒绝。
提议分布为给定状态
时提出状态
的条件概率,接受分布
为接受所提出的状态
的概率。转换概率就能写成它们的乘积:
(2)
由(1)和(2)就有:
之后就要选一个满足上面条件的接受函数了。一般我们选Metropolis选项,即:
满足了Metropolis算法的基本步骤,即大于1的时候总是接受,小于1的时候按比例接受和拒绝。
则Metropolis-Hastings算法可以概述为:
-
初始化:随机选取初始状态
-
根据
随机选取状态
-
根据
选择接受或拒绝状态
;若接受,系统转换到状态
,否则停留在状态
-
返回步骤2,直到生成了
个状态
-
保存状态
,返回步骤2
原则上说,被保存的状态是从分布中生成的,因为步骤4保证了这些状态是非相关的。取值
需根据不同的特性选取,如提出的分布以及,它必须是Markov过程自相关时间的阶。
关于的选取需具体问题具体分析和调整。
MCMC使您可以从实际上不可能完全定义的概率分布中进行采样!
令人惊讶的是,MCMC的核心并不难于描述或实施。让我们看一个简单的MCMC算法。
Metropolis-Hastings算法
该算法与模拟退火算法非常相似。
MH算法可以表示为:
Prob(acceptB | A)= min(1,Posterior(B)Posterior(A)⋅Prob(b→a)Prob(a→b))
请注意,从本质上讲,这与“ Metropolis”模拟退火算法相同,后验概率代替了概率,并且 k 参数设置为1。
二元正态例子
视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
视频
什么是Bootstrap自抽样及R语言Bootstrap线性回归预测置信区间
请记住,MCMC采样器只是随机数生成器的一种。我们可以使用Metropolis-Hastings采样器来开发自己的随机数生成器,生成进行简单的已知分布。在此示例中,我们使用MH采样器从标准双变量正态概率分布生成随机数。
对于这个简单的示例,我们不需要MCMC采样器。一种实现方法是使用以下代码,该代码从具有相关参数ρ的双变量标准正态分布中绘制并可视化任意数量的独立样本。
#################
#MCMC采样的简单示例
#################
#########
# #首先,让我们构建一个从双变量标准正态分布生成随机数的函数
rbvn<-function (n, rho) #用于从二元标准正态分布中提取任意数量的独立样本。
{
x <- rnorm(n, 0, 1)
y <- rnorm(n, rho * x, sqrt(1 - rho^2))
cbind(x, y)
}
#########
# 现在,从该分布图中绘制随机抽样
bvn<-rbvn(10000,0.98)
par(mfrow=c(3,2))
plot(bvn,col=1:10000
###############
# #Metropolis-Hastings双变量正态采样器的实现...
library(mvtnorm) # 加载一个包,该包使我们能够计算mv正态分布的概率密度
metropoli<- function (n, rho=0.98){ # 双变量随机数生成器的MCMC采样器实现
mat <- matrix(ncol = 2, nrow = n) # 用于存储随机样本的矩阵
x <- 0 # 所有参数的初始值
prev <- dmvnorm(c(x,y),mean=c(0,0),sig
# 起始位置分布的概率密度
mat[1, ] <- c(x, y) # 初始化马尔可夫链
newx <- rnorm(1,x,0.5) # 进行跳转
newprob <- dmvnorm(c(newx,newy),sigma =
# 评估跳转
ratio <- newprob/prev # 计算旧位置(跳出)和建议位置(跳到)的概率之比。
prob.accept <- min(1,ratio) # 决定接受新跳跃的概率!
if(rand<=prob.accept){
x=newx;y=newy # 将x和y设置为新位置
mat[counter,] <- c(x,y) # 将其存储在存储阵列中
prev <- newprob # 准备下一次迭代
然后,我们可以使用MH采样器从该已知分布中获取随机样本…
###########
# 测试新的M-H采样器
bvn<-metropoli(10000,0.98)
par(mfrow=c(3,2))
plot(bvn,col=1:10000)
plot(bvn,type=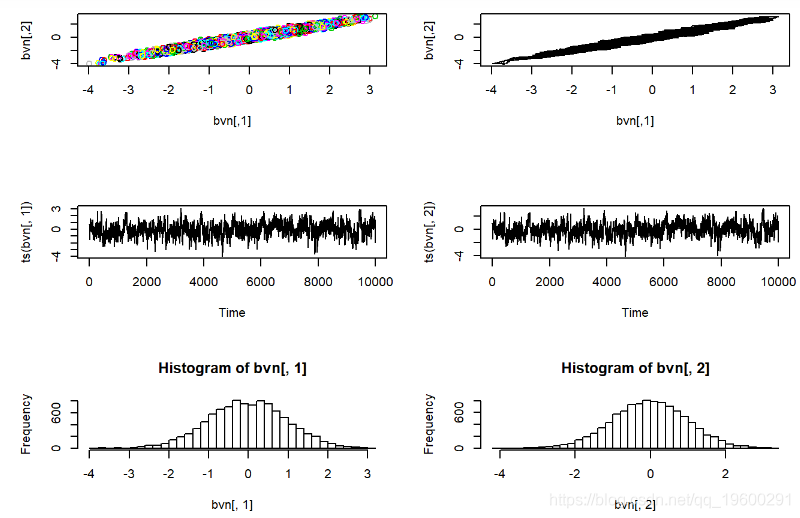
让我们尝试解决一个问题。
MCMC对粘液瘤病进行调查
############
#黏液病示例的MCMC实现
############
subset(MyxDat,grade==1## grade day titer
## 1 1 2 5.207
## 2 1 2 5.734
## 3 1 2 6.613
## 4 1 3 5.997
## 5 1 3 6.612
## 6 1 3 6.810选择使用Gamma分布。这是经验分布:
############ 第100次可视化粘液病数据
hist(Myx$titer,freq=FALSE)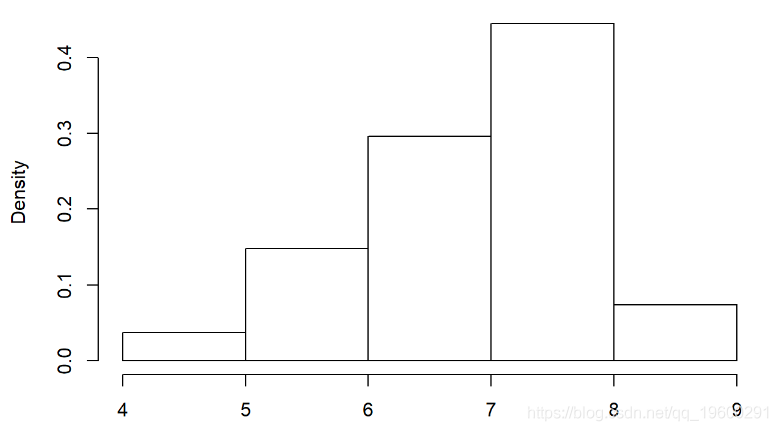
我们需要估算最适合此经验分布的伽马比率和形状参数。这是适合此分布的Gamma的一个示例:
#########
# ...覆盖生成模型的数据(伽玛分布)
curve(dgamma(x,shape=40,scale=0.15),add=T,col="red")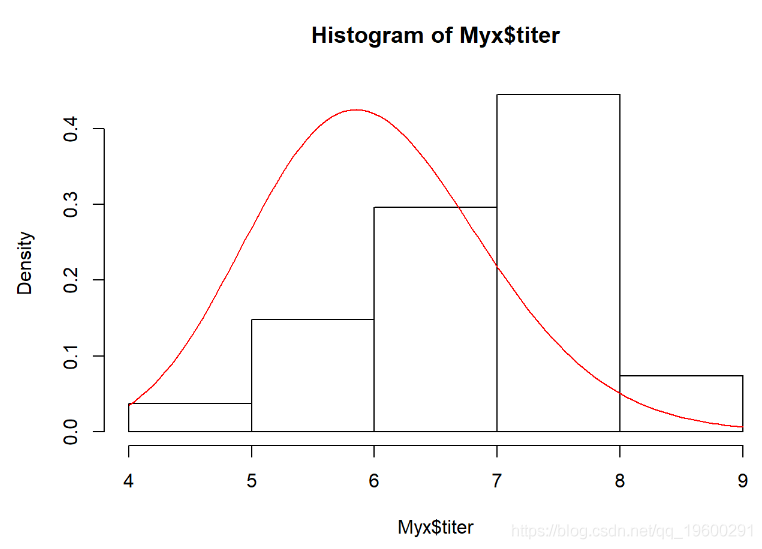
二维(对数)似然面:
##############
# 定义二维参数空间
##############
shapevec <- seq(3,100,by=0.1)
scalevec <- seq(0.01,0.5,by=0.001)
##############
# #定义参数空间内此网格上的似然面
##############
GammaLogLikelihoodFunction <- function(par
}
surface2D <- matrix(nrow=length(shapevec),ncol=length(scalevec)) #初始化存储变量
newparams <- c(sha
surface2D[i,j] <- GammaLogLikelihoodFunction(newparams)
############
# 可视化似然面
############
contour(x=shapevec,y=scalevec,z=surface2D,levels=c(-30,-40,-80,-500),add=T)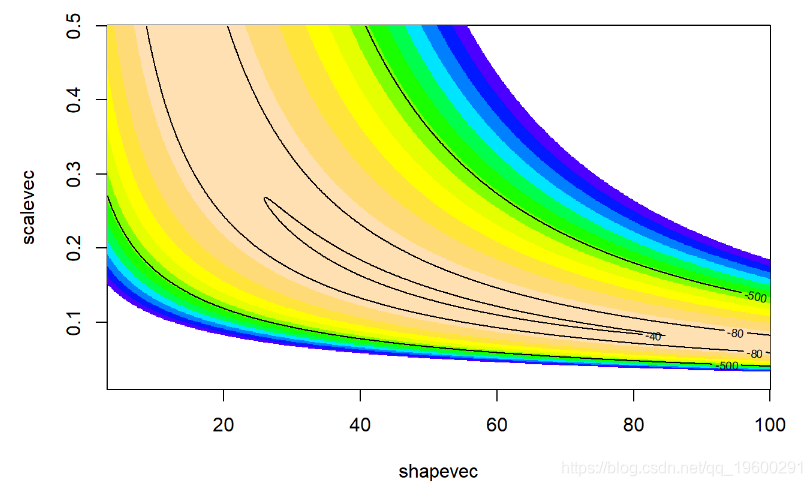
这是MH算法的实现,用于找到后验分布!
首先,我们需要一个似然函数–这次,我们将返回真实概率–而不是对数转换的概率
############
#编写非对数转换的似然函数
GammaLike- function(params){
prod(dgamma(Myx$titer,shape=params['shape']
params <- c(shape=40,## shape scale ## 40.00 0.15GammaLike(params)随时关注您喜欢的主题
## [1] 2.906766e-22GammaLogLike(params)## [1] -49.58983然后,我们需要预先分配参数!在这种情况下,我们分配gamma(shape = 0.01,scale = 100)和gamma(shape = 0.1,scale = 10)的分布(均值为1且方差略低):
#############
# 函数返回参数空间中任意点的先验概率密度
GammaPriorFunction <- function(params){
prior <- c(shape=NA,scale=NA)
],3,100)
# prior['scale'] <- dunif(params['
GammaLogPriorFunction <- function(params){
prior <- c(shape=NA,scale=NA)
'],shape=0.001,scale=1000,log=T)
# prior['shape'] <- dunif(params['shape'],3,100)
# prior['scale'] <- dunif(params['
curve(dgamma(x,shape=0.01,scale=1000),3,100)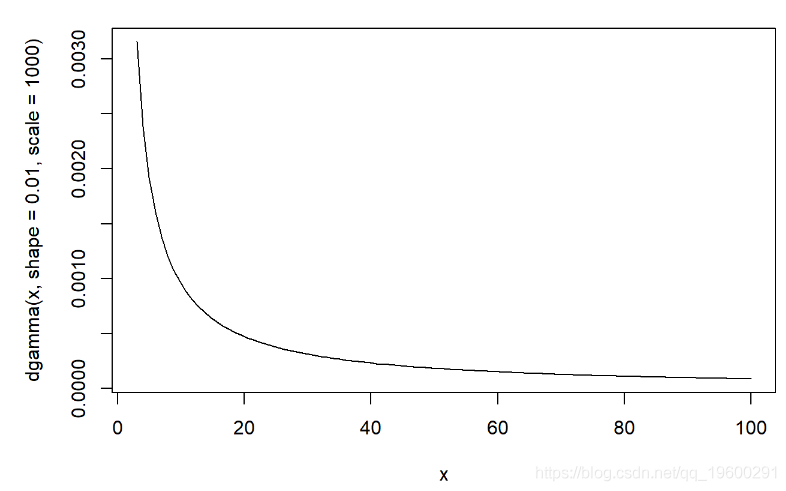
params## shape scale ## 40.00 0.15GammaPrior(params)## [1] 1.104038e-06prior2D <- matrix(nrow=length(shapevec),ncol=length(scalevec)) # 初始化存储变量
newparams <- c(shape=50,scale=0
for(j in 1:length(scalevec)){
newparams['scale'] <- sca
############
# 可视化似然面
############
image(x=shapevec,y=scalevec,z=prior2D,zlim 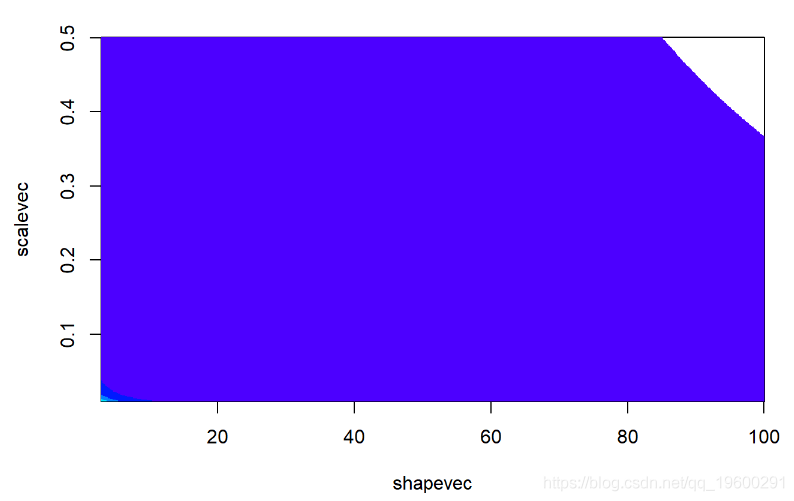
contour(x=shapevec,y=scalevec,z=prior2D,levels=c(-30,-40,-80,-500),add=T)然后,我们需要一个函数,该函数可以计算参数空间中任何给定跳转的后验概率比率。因为我们正在处理 后验概率的 比率,所以 我们不需要计算归一化常数。
我们假设形状和比例 在先验中是 独立的(联合先验的乘法概率)。然而,并没有对后验参数相关性提出相同的假设,因为概率可以反映在后验分布中。
无需归一化常数,我们只需要计算加权似然比(即先验加权的似然比)
############
# 函数用于计算参数空间中任意两点之间的后验密度比
PosteriorRatio <- function(oldguess,newguess
oldLik <- max(1e-90,GammaLikelihoodFunction(oldguess)) # 计算旧猜测的可能性和先验密度
newLik <- GammaLikelihoodFunction(newguess) # 在新的猜测值下计算可能性和先验密度
return((newLik*newPrior)/(oldLik*oldPrior)) # 计算加权似然比
}
PosteriorRatio2 <- function(oldguess,newguess){
oldLogLik <- GammaLogLikelihoodFunction(oldguess) # 计算旧猜测的可能性和先验密度
newLogLik <- GammaLogLikelihoodFunction(newguess) # 在新的猜测值下计算可能性和先验密度
return(exp((newLogLik+newLogPrior)-(oldLogLik+oldLogPrior))) # 计算加权似然比
}## [1] 0.01436301PosteriorRatio2(oldguess,newguess)## [1] 0.01436301然后,我们需要一个函数进行新的推测或在参数空间中跳转:
############
# 为参数空间中的跳转定义:使用正态分布函数进行新的推测
newGuess <- function(oldguess)
jump <- c(shape=rnorm(1,mean=0,sd=sdshapejump),scale=rnorm(1,0,sdscalejump))
newguess <- abs(oldguess + ju
}
# 在原始推测附近设置新的推测
newGuess(oldguess=params) ## shape scale
## 35.7132110 0.1576337newGuess(oldguess=params)## shape scale
## 45.1202345 0.2094243newGuess(oldguess=params)## shape scale
## 42.87840436 0.08152061现在,我们准备实现Metropolis-Hastings MCMC算法:
我们需要一个初始点:
########### 在参数spacer中设置起点
startingvals <- c(shape=75,scale=0.28) # 算法的起点测试函数
############ 尝试我们的新函数
newguess <- newGuess(startingvals)
# 在参数空间中跳跃newguess## shape scale
## 73.9663949 0.3149796PosteriorRatio2(startingvals,newguess)
# 后验比例差异## [1] 2.922783e-57现在让我们看一下Metropolis-Hastings:
###############
#可视化Metropolis-Hastings
chain.length <- 11
gth,ncol=2)
colnames(guesses) <- names(startingvals)
guesses[1,] <- startingvals
counter <- 2
post.rat <- PosteriorRatio2(oldguess,newguess)
prob.accept <- min(1,post
oldguess <- newguess
guesses[coun
#可视化
contour(x=shapevec,y=scal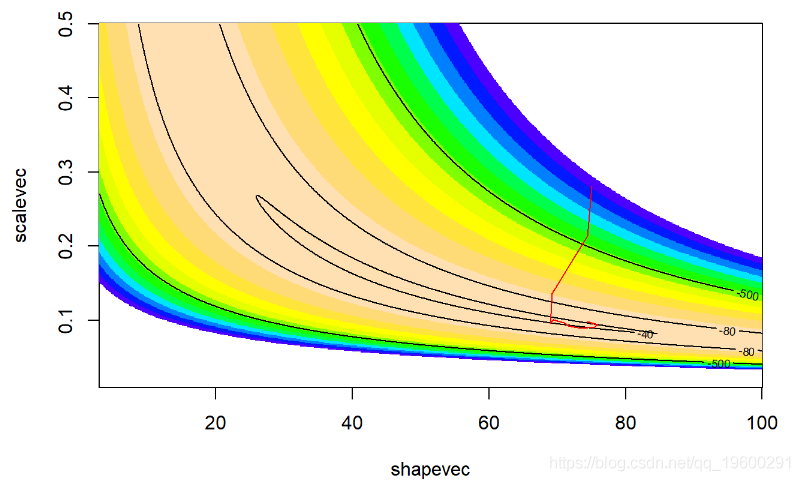
我们运行更长的时间
##########
# 获取更多MCMC示例
chain.length <- 100
oldgu
counter <- 2
while(counter <= chain.length){
newguess <- newGuess(oldguess)
post.rat <- Posterio
rand <- runif(1)
if(rand<=prob.accept){
ewguess
counter=counte
#可视化
image(x=shapevec,y=scalevec,z=su
urface2D,levels=c(-30,-40,-80,-5
lines(guesses,col="red")更长的时间
############
#更长的时间
chain.length <- 1000
oldguess <- startingvals
chain.length,ncol=2)
colnames(guesses) <- names(startingvals)
guesses[1,] <- startingva
ess)
post.rat <- PosteriorRatio2(oldguess,newguess)
prob.accept <- min(1,post.rat)
rand <- runif(1)
guesse
#可视化
image(x=shapevec,y=scalevec,
rface2D,levels=c(-30,-40,-80,-500),a看起来更好!搜索算法可以很好地找到参数空间的高似然部分!
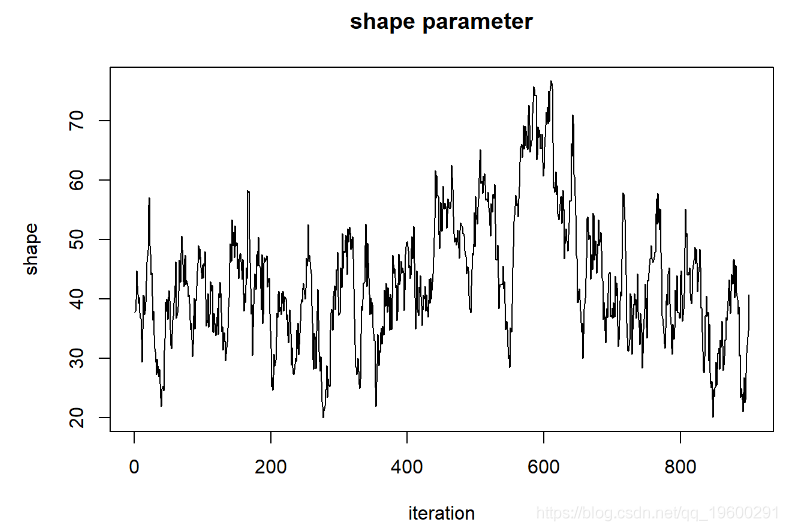
现在,让我们看一下“ shape”参数的链
#############
# 评估MCMC样本的“轨迹图” ...
##### Shape 参数
plot(1:chain.length,guesses[,'sha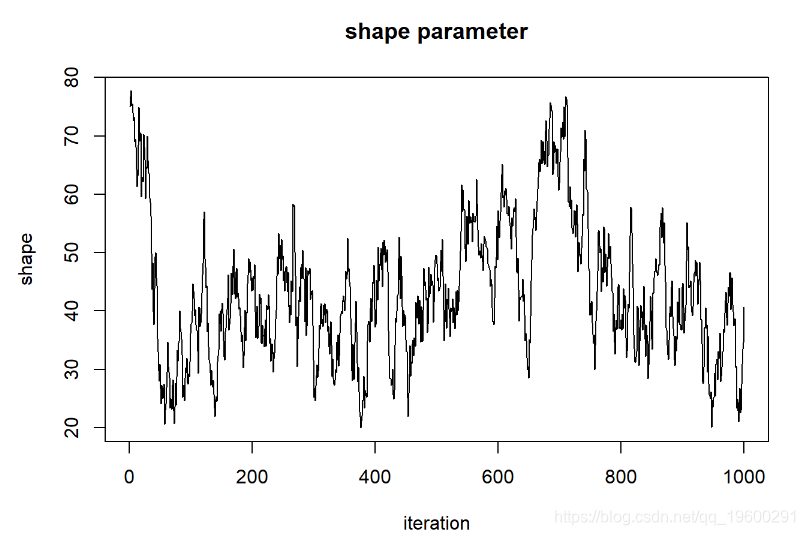
对于比例参数
###### 比例参数
plot(1:chain.length,guesses[,'scale'],type="l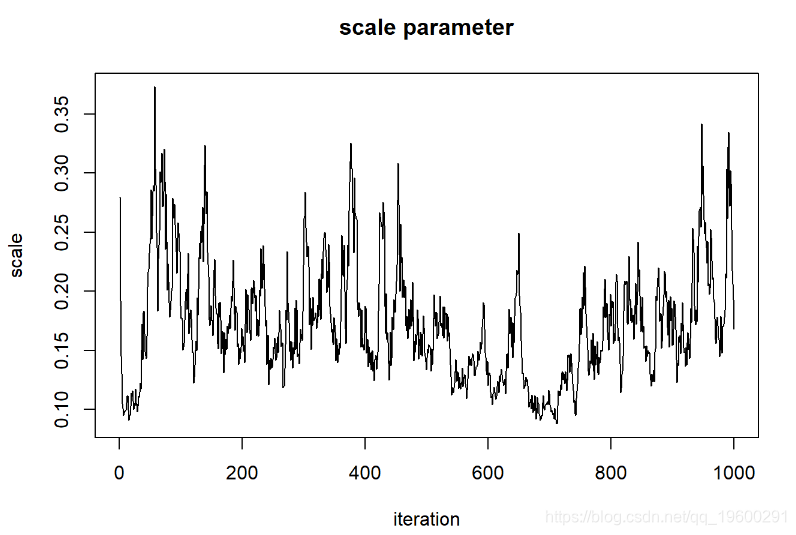
我们可以说这些链已经收敛于形状参数的后验分布吗?
首先,链的起点“记住”起始值,因此不是固定分布。我们需要删除链的第一部分。
############
# 删除预烧期(允许MCMC有一段时间达到后验概率)
burn.in <- 100
MCMCsamples <- guesses[-c(1:burn.in),]
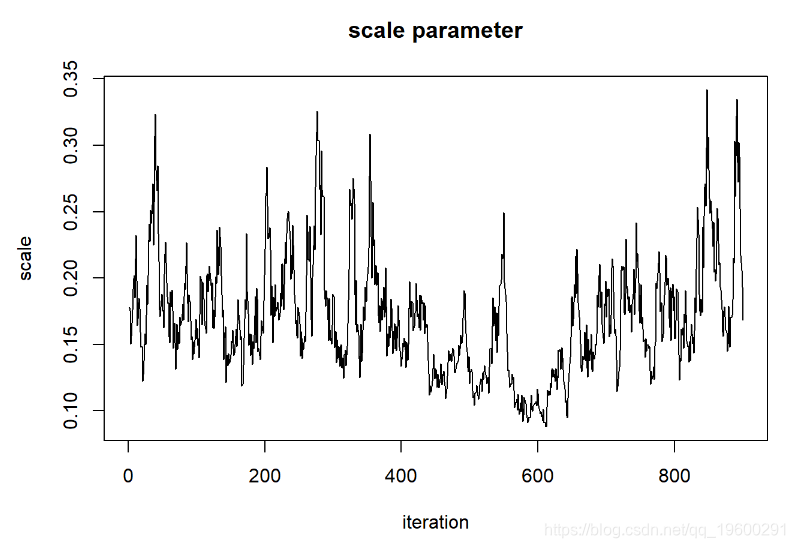
但这看起来还不是很好。让我们运行更长的时间,看看是否得到的东西看起来更像是随机数生成器(白噪声)
##########
# 再试一次-运行更长的时间
chain.length <- 20000
oldguess <- startingv
o2(oldguess,newguess)
prob.accept <- mi
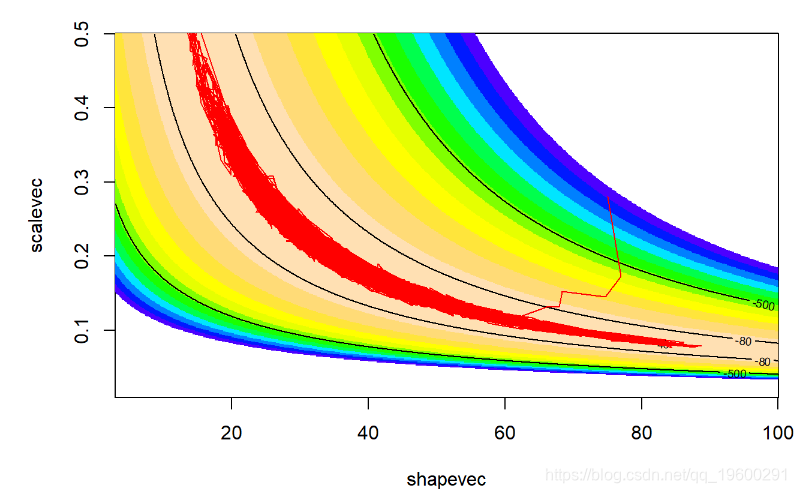
让我们首先删除前5000个样本作为预烧期
############## 使用更长的“预烧”
burn.in <- 5000
MCMCsamples <- guesses[-c(1:bur现在,让我们再次看一下链条
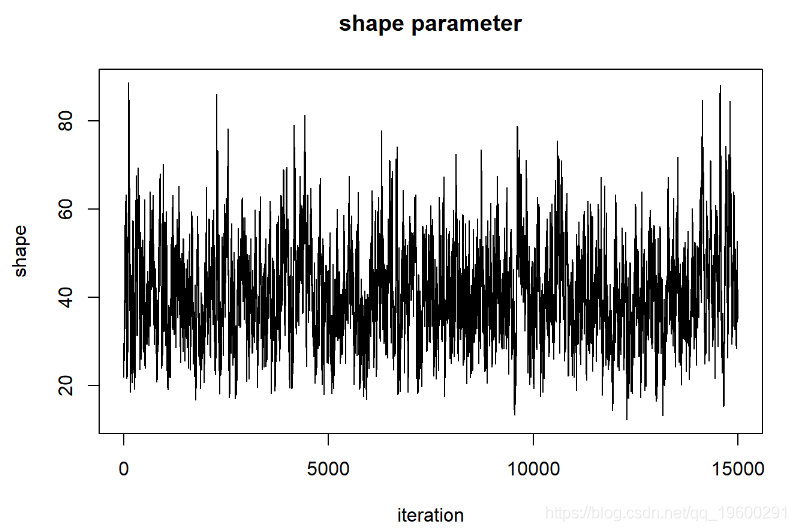
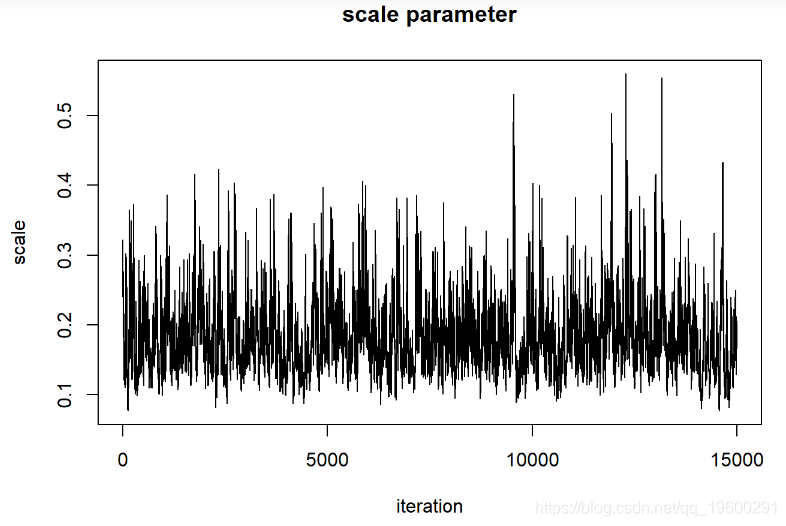
在评估这些迹线图时,我们希望看到看起来像白噪声的“平稳分布”。该轨迹图看起来可能具有一些自相关。解决此问题的一种方法是稀疏MCMC样本:
########### “稀疏” MCMC样本
thinnedMCMC <- MCMCsamples[seq(1,chain.length,by=5),]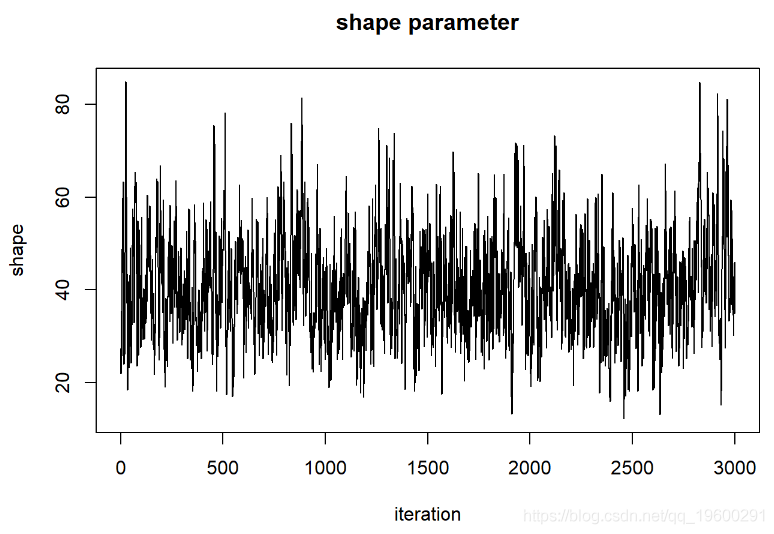
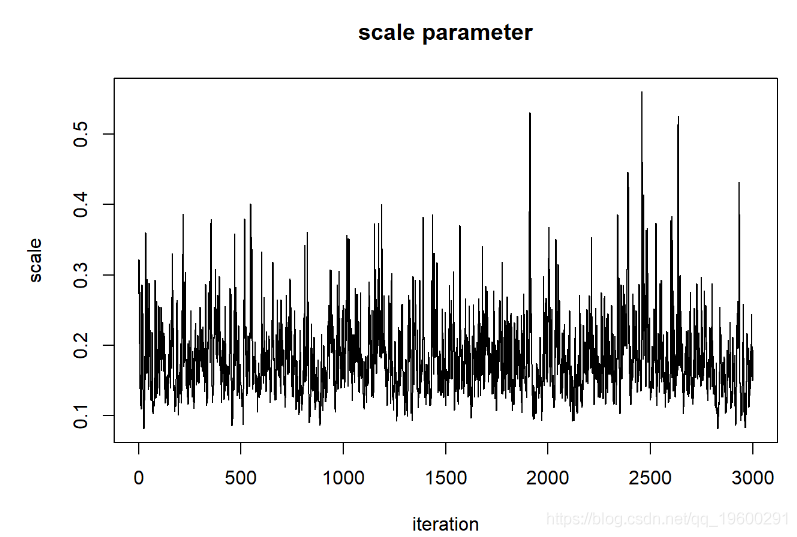
现在我们可以检查我们的后验分布!
# 可视化后验分布
plot(density(thinnedMCMC[,'scale'])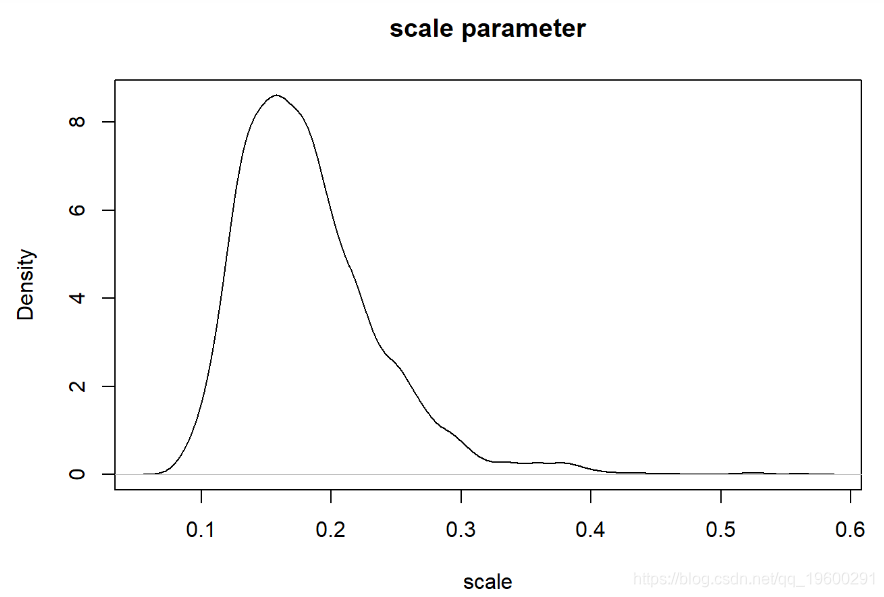
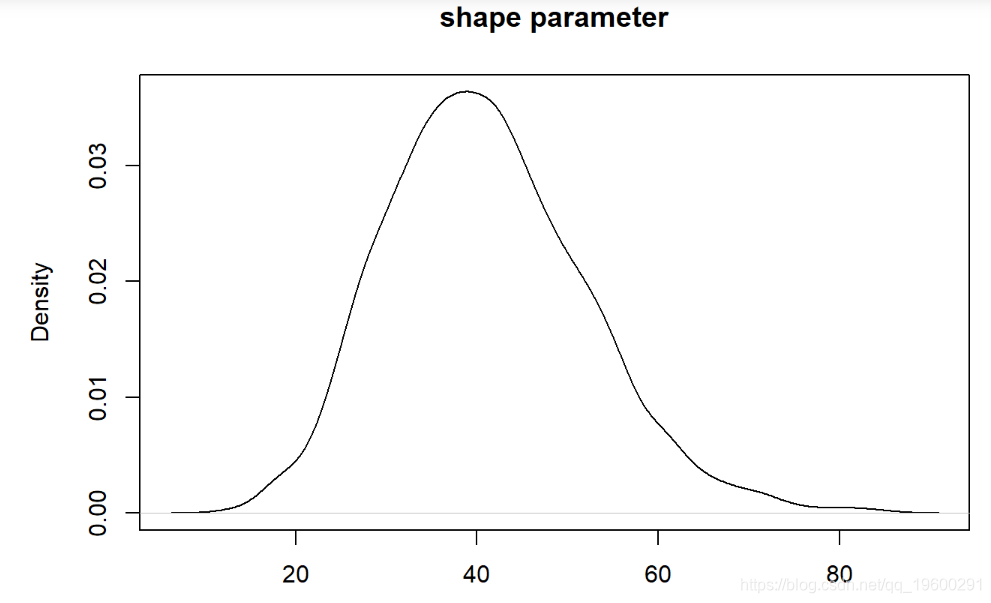
我们可以像以前一样可视化。
#########
# 更多后验概率检察
par(mfrow=c(3,2))
plot(thinnedMCMC,col=1:10000)
plot(thinnedMCMC,type="l")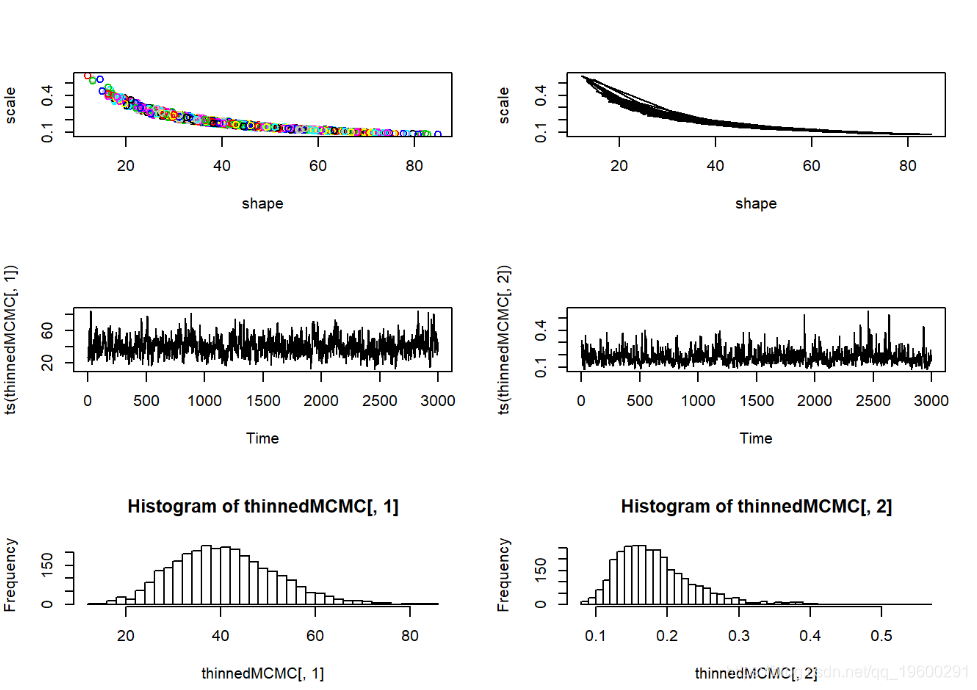
可以修改Metropolis-Hastings MCMC方法来拟合任意模型的任意数量的自由参数。但是,MH算法本身不一定是最有效和灵活的。在实验中,我们使用吉布斯采样,大多采用建模语言 BUGS 。
注意:BUGS实现(例如JAGS)实际上倾向于结合使用MH和Gibbs采样,MH和Gibbs采样器并不是唯一的MCMC例程。例如,“ stan”使用MH采样的一种改进形式,称为“ Hamiltonian Monte Carlo”。
吉布斯Gibbs采样器
Gibbs采样器非常简单有效。基本上,该算法从完整的条件 概率分布(即, 在模型中所有其他参数的已知值作为条件的条件下,对任意参数i的后验分布)中进行 连续采样 。
在很多情况下,我们不能直接制定出我们的模型后验分布,但我们 可以 分析出条件后验分布。尽管如此,即使它在分析上不易处理,我们也可以使用单变量MH程序作为最后方法。
问:为什么Gibbs采样器通常比纯MH采样器效率更高?
二元正态例子
MCMC采样器只是随机数生成器的一种。我们可以使用Gibbs采样器来开发自己的随机数生成器,以实现相当简单的已知分布。在此示例中,我们使用Gibbs采样器从标准双变量正态概率分布生成随机数。注意,吉布斯采样器在许多方面都比MH算法更简单明了。
#############
#Gibbs采样器的简单示例
#############
########
# 首先,回顾一下我们简单的双变量正态采样器
rbvn<-function (n, rho){ #f函数用于从双变量标准正态分布中提取任意数量的独立样本。
x <- rnorm(n, 0, 1)
y <- rnorm(n, rho * x, sqrt(1 - rho^2))
#############
# 现在构造一个吉布斯采样器
gibbs<-function (n, rho){ # 双变量随机数生成器的gibbs采样器实现
mat <- matrix(ncol = 2, nrow = n) # 用于存储随机样本的矩阵
mat[1, ] <- c(x, y) # initialize the markov chain
for (i in 2:n) {
x <- rnorm(1, rho * y, sqrt(1 - rho^2)) # 以y为条件的x中的样本
y <- rnorm(1, rho * x, sqrt(1 - rho^2)) # 以x为条件的y中的样本
mat[i, ] <- c(x, y)
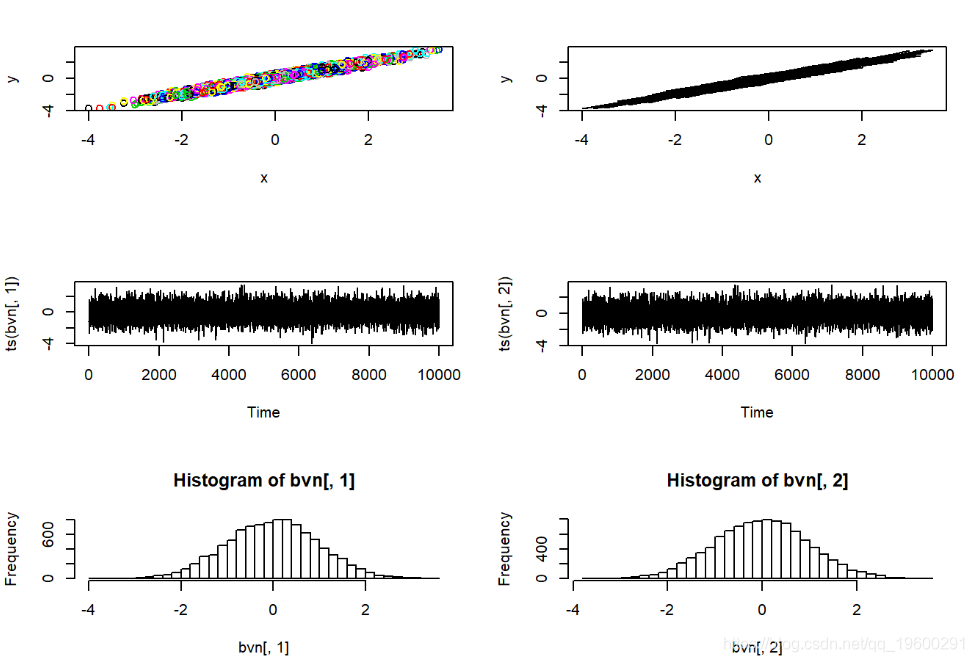
然后,我们可以使用Gibbs采样器从该已知分布中获取随机样本…
##########
# 测试吉布斯采样器
plot(ts(bvn[,2]))
hist(bvn[,1],40)
hist(bvn[,2],40)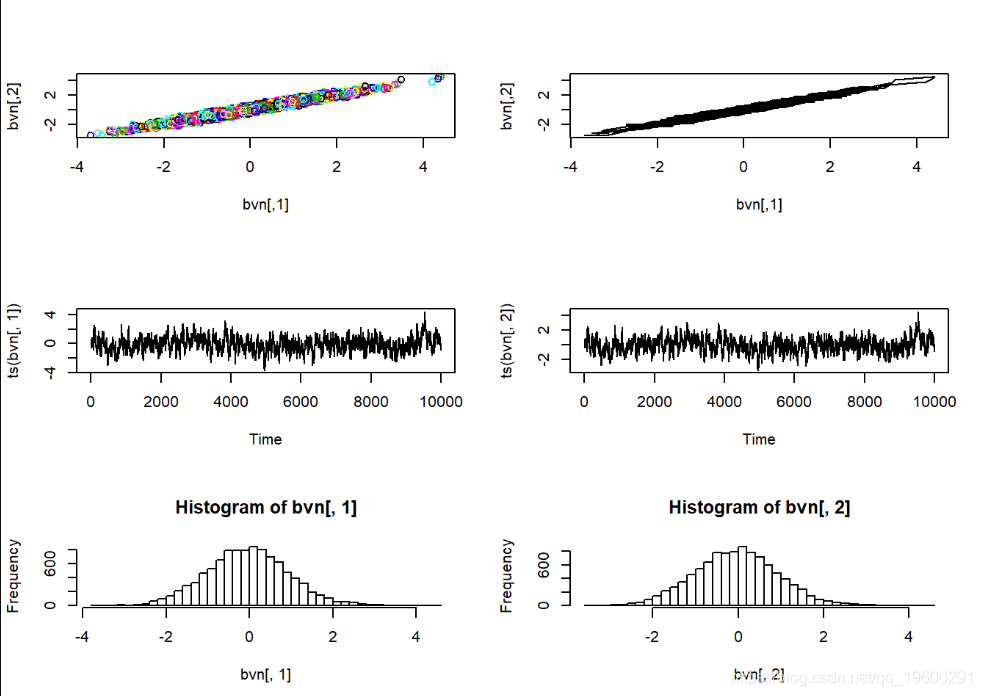
在这里,马尔可夫链的样本中有很多明显的自相关。Gibbs采样器经常有此问题。
示例
BUGS语言
最后,让我们为我们最喜欢的粘瘤病示例创建一个Gibbs采样器,为此,我们将使用BUGS语言(在JAGS中实现)来帮助我们!
JAGS,全称是Just another Gibbs sampler,是基于BUGS语言开发的利用MCMC来进行贝叶斯建模的软件包。它没有提供建模所用的GUI以及MCMC抽样的后处理,这些要在其它的程序软件上来处理,比如说利用R包(rjags)来调用JAGS并后处理MCMC的输出。JAGS相对于WinBUGS/OpenBUGS的主要优点在于平台的独立性,可以应用于各种操作系统,而WinBUGS/OpenBUGS只能应用于windows系统;JAGS也可以在64-bit平台上以64-bit应用来进行编译。
BUGS语言看起来与R类似,但是有几个主要区别:
- 首先,BUGS是一种编译语言,因此代码中的操作顺序并不重要
- BUGS不是矢量化的-您需要使用FOR循环
- 在BUGS中,几个概率分布的参数差异很大。值得注意的是,正态分布通过均值和精度(1 / Variance )进行参数化。
这是用BUGS语言实现的粘液病示例:
model {
#############
# 似然
############
for(obs in 1:n.observations){
titer[obs] ~ dgamma(shape,rate
#############
# 先验
############
rate <- 1/scale # 将BUGS的scale参数转换为“ rate”
}我们可以使用R中的“ cat”函数将此模型写到您的工作目录中的文本文件中:
###########
# BUGS建模语言中的粘液瘤示例
##########
# 将BUGS模型写入文件
cat("
model {
#############
# 似然
############
for(obs in 1:n.observations){
titer[obs] ~ dgamma(shape,rate)
#############
# 先验
############
shape ~ dgamma(0.001,0.001
file="BUGSmodel.txt")现在我们已经将BUGS模型打包为文本文件,我们将数据捆绑到一个列表对象中,该列表对象包含BUGS代码中引用的所有相关数据:
############
# 将数据封装到单个“列表”对象中
myx.data <- list(
n.observations = length(Myx$titer## $titer
## [1] 5.207 5.734 6.613 5.997 6.612 6.810 5.930 6.501 7.182 7.292 7.819
## [12] 7.489 6.918 6.808 6.235 6.916 4.196 7.682 8.189 7.707 7.597 7.112
## [23] 7.354 7.158 7.466 7.927 8.499
##
## $n.observations
## [1] 27然后,我们需要为所有参数定义初始值。将其定义为一个函数很方便,因此可以使用不同的起始值来初始化每个MCMC链。
############ 用于为所有自由参数生成随机初始值的函数 init.vals.for.bugs()## $shape
## [1] 51.80414
##
## $scale
## [1] 0.2202549init.vals.for.bugs()## $shape
## [1] 89.85618
##
## $scale
## [1] 0.2678733init.vals.for.bugs()## $shape
## [1] 69.22457
##
## $scale
## [1] 0.1728908现在我们可以调用JAGS!
###########
# 运行 JAGS
############ Loading required package: rjags## The following object is masked from 'package:coda':## ## traceplot jags.fit <- run.jags(model="BUGSmodel.txt",## Compiling rjags model...
## Calling the simulation using the rjags method...
## Adapting the model for 100 iterations...
## Running the model for 5000 iterations...
## Simulation complete
## Finished running the simulationjags.fit) # 转换为“ MCMC”对象(CODA包) ##
## Iterations = 101:5100
## Thinning interval = 1
## Number of chains = 3
## Sample size per chain = 5000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## shape 51.6013 14.36711 0.1173070 2.216657
## scale 0.1454 0.04405 0.0003597 0.006722
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## shape 28.76333 40.9574 50.1722 60.2463 82.7532
## scale 0.08346 0.1148 0.1378 0.1687 0.2389plot(jagsfit.mcmc)评估收敛
第一步是视觉检查-我们寻找以下内容来评估收敛性:
- 当视为“轨迹图”时,每个参数的链应看起来像白噪声(模糊的毛毛虫)或类似的噪声
- 多个具有不同起始条件的链条看起来应该相同
我们可能在这里可以做得更好的一种方法是使链条运行更长的时间,并丢弃初始样本我们还可以。
通过细化链来尝试减少自相关,我们每20个样本中仅保留1个。
################
#运行链更长时间
jags.fit <-
sample = 10000,n.chains = 3,adapt = 1000,burnin = 1000,
summarise = FALSE,thin=20,method = "parallel" )## Calling 3 simulations using the parallel method...
## Following the progress of chain 1 (the program will wait for all
## chains to finish before continuing):
## Welcome to JAGS 4.2.0 on Wed Oct 23 11:33:35 2019
## JAGS is free software and comes with ABSOLUTELY NO WARRANTY
## Loading module: basemod: ok
## Loading module: bugs: ok
## . . Reading data file data.txt
## . Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 27
## Unobserved stochastic nodes: 2
## Total graph size: 37
## . Reading parameter file inits1.txt
## . Initializing model
## . Adapting 1000
## -------------------------------------------------| 1000
## ++++++++++++++++++++++++++++++++++++++++++++++++++ 100%
## Adaptation successful
## . Updating 1000
## -------------------------------------------------| 1000
## ************************************************** 100%
## . . . Updating 200000
## -------------------------------------------------| 200000
## ************************************************** 100%
## . . . . Updating 0
## . Deleting model
## .
## All chains have finished
## Simulation complete. Reading coda files...
## Coda files loaded successfully
## Finished running the simulationjagsfit.mcmc <- as.mcmc.list
# 转换为“ MCMC”对象(CODA包)
##
## Iterations = 2001:201981
## Thinning interval = 20
## Number of chains = 3
## Sample size per chain = 10000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## shape 47.1460 12.9801 0.0749404 0.292218
## scale 0.1591 0.0482 0.0002783 0.001075
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## shape 25.14757 37.9988 45.9142 55.1436 75.5850
## scale 0.09147 0.1256 0.1509 0.1825 0.2773plot(jagsfit.mcmc)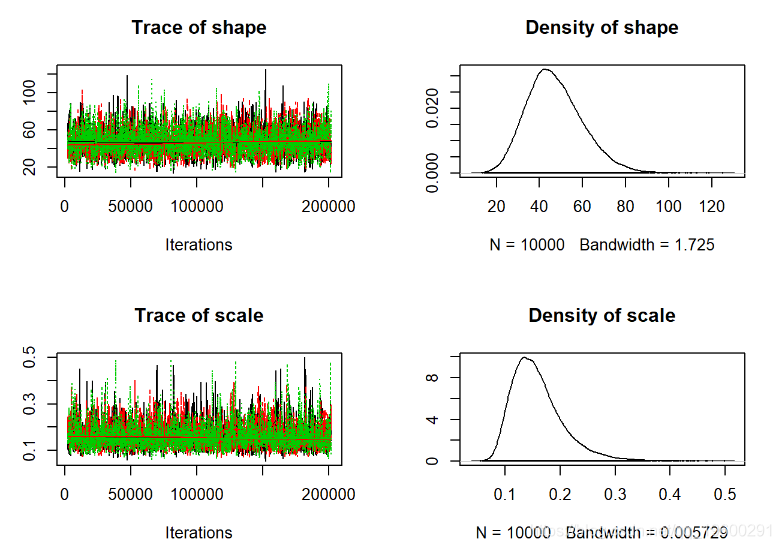
从视觉上看,这看起来更好。现在我们可以使用更多的定量收敛指标。
Gelman-Rubin诊断
一种简单而直观的收敛诊断程序是 Gelman-Rubin诊断程序,该诊断程序基于简单的蒙特卡洛误差来评估链之间是否比应有的链距更大:
##############
# 运行收敛诊断
gelman(jagsfit.mcmc)## Potential scale reduction factors:
##
## Point est. Upper C.I.
## shape 1 1.00
## scale 1 1.01
##
## Multivariate psrf
##
## 1通常,1.1或更高的值被认为收敛不佳。为模型中的所有可用参数计算GR诊断。如果测试失败,则应尝试运行更长的链!
所以这个模型看起来不错!
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据 【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用
【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用 Python电影票房预测模型研究——贝叶斯岭回归Ridge、决策树、Adaboost、KNN分析猫眼豆瓣数据
Python电影票房预测模型研究——贝叶斯岭回归Ridge、决策树、Adaboost、KNN分析猫眼豆瓣数据 视频讲解|核密度估计朴素贝叶斯:业务数据分类—从理论到实践
视频讲解|核密度估计朴素贝叶斯:业务数据分类—从理论到实践



