比如说分类变量为是否幸存、是因变量，连续变量为年龄、是自变量，这两者可以做相关分析吗？两者又是否可以做回归分析？
我们考虑泰坦尼克号数据集，考虑两个变量，年龄x（连续变量）和幸存者指标y（分类变量）
考虑泰坦尼克号数据集，
titanic = titanic[!is.na(titanic$Age),]
attach(titanic)考虑两个变量，年龄x（连续变量）和幸存者指标y（分类变量）
1.皮尔逊相关系数：
适用条件：① 连续性变量，②变量服从正态分布，③ 标准差不为0
2.斯皮尔曼相关系数：
(n为等级个数，d为等级差数）
适用条件：①连续性、分类型变量
注：连续性变量利用该算法会出现精确度下降，计算出相关系数需要查表常看对应样本下的相关系数
3.kendall相关系数：
(无结的情况下使用该计算方式)
2. (有结的情况下使用该计算方式)
，为i行中的结
,为j列中的结
3.
注： :顺序一致的变量，
顺序不一致的变量
适用条件：①连续性、分类型变量
m是min(i,j)
4.PMI点互信息指数：衡量两个二分变量之间的相关性,主要应用在文本分析中，0-1之间为相关，-1-0之间为不想关互斥，0为不不相关也不互斥
其中，条件概率公式为：
X = Age
Y = Survived年龄可能是逻辑回归中的有效解释变量，
summary(glm(Survived~Age,data=titanic,family=binomial))
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.05672 0.17358 -0.327 0.7438
Age -0.01096 0.00533 -2.057 0.0397 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 964.52 on 713 degrees of freedom
Residual deviance: 960.23 on 712 degrees of freedom
AIC: 964.23此处的显着性检验的p值略低于4％。
实际上，可以将其与偏差值（零偏差和残差）相关联。
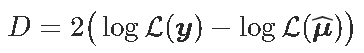
而
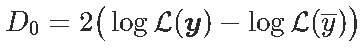
在x没有影响的假设下，D_0趋于具有1个自由度的χ2分布。我们可以计算似然比检验的p值自由度，
1-pchisq(
[1] 0.03833717与高斯检验一致。但是如果我们考虑非线性变换
glm(Survived~bs(Age)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.8648 0.3460 2.500 0.012433 *
bs(Age)1 -3.6772 1.0458 -3.516 0.000438 ***
bs(Age)2 1.7430 1.1068 1.575 0.115299
bs(Age)3 -3.9251 1.4544 -2.699 0.006961 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 964.52 on 713 degrees of freedom
Residual deviance: 948.69 on 710 degrees of freedomAge的p值更小，似乎“更重要”
[1] 0.001228712为了可视化非零相关性，可以考虑给定y = 1时x的条件分布，并将其与给定y = 0时x的条件分布进行比较，
Two-sample Kolmogorov-Smirnov test
data: X[Y == 0] and X[Y == 1]
D = 0.088777, p-value = 0.1324
alternative hypothesis: two-sided即p值大于10％时，两个分布没有显着差异。
v= seq(0,80
v1 = Vectorize(F1)(vx)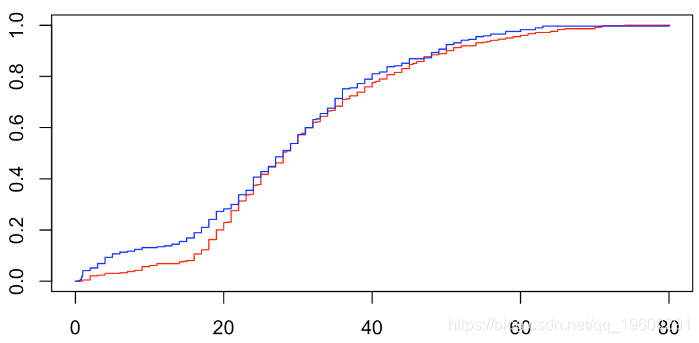
我们可以查看密度
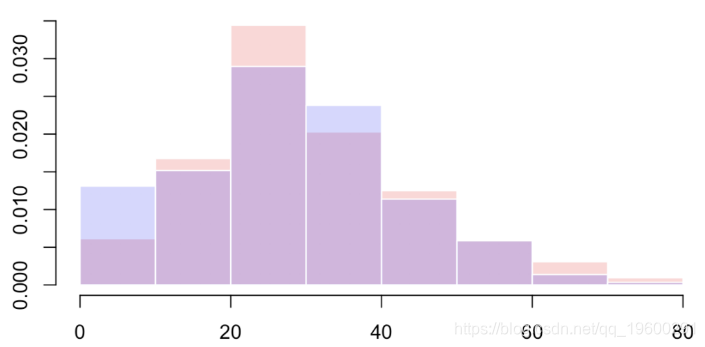
另一种方法是离散化变量x并使用Pearson的独立性检验，
table(Xc,Y)
Y
Xc 0 1
(0,19] 85 79
(19,25] 92 45
(25,31.8] 77 50
(31.8,41] 81 63
(41,80] 89 53
Pearson's Chi-squared test
data: table(Xc, Y)
X-squared = 8.6155, df = 4, p-value = 0.07146p值在此处为7％，分为年龄的五个类别。实际上，我们可以比较p值
pvalue = function(k=5){
LV = quantile(X,(0:k)/k)
plot(k,p,type="l")
abline(h=.05,col="red",lty=2)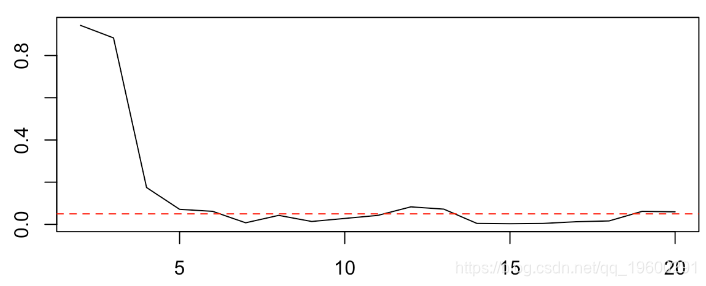
只要我们有足够的类别，P值就会接近5％。实际上年龄在试图预测乘客是否幸存时是一个重要的变量。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python酒店预订数据：随机森林与逻辑回归模型ROC曲线可视化
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
Python谷歌商店Google Play APP评分预测：LASSO、多元线性回归、岭回归模型对比研究
Python糖尿病预测融合模型构建：伯努利朴素贝叶斯、逻辑回归、决策树、随机森林、支持向量机SVM应用
