本文的目标是使用各种预测模型预测Google的未来股价,然后分析各种模型。
Google股票数据集是使用R中的Quantmod软件包从Yahoo Finance获得的。
可下载资源
视频
K近邻KNN算法原理与R语言结合新冠疫情对股票价格预测
预测算法是一种试图根据过去和现在的数据预测未来值的过程。提取并准备此历史数据点,来尝试预测数据集所选变量的未来值。在市场历史期间,一直有一种持续的兴趣试图分析其趋势,行为和随机反应。
传统上,使用统计方法(例如ARIMA模型或指数平滑)进行时间序列预测。但是,最近几十年出现了使用计算智能技术来预测时间序列。尽管人工神经网络是用于时间序列预测的最杰出的机器学习技术,但其他方法如高斯过程或KNN等也已应用。本文重点讲讲用KNN方法做时间序列预测。
KNN算法又称 k k k近邻分类(k-nearest neighbor classification)算法。它是根据不同特征值之间的距离来进行分类的一种简单的机器学习方法,它是一种简单但是懒惰的算法。他的训练数据都是有标签的数据,即训练的数据都有自己的类别。KNN算法主要应用领域是对未知事物进行分类,即判断未知事物属于哪一类,判断思想是,给出一个新的样本,KNN根据如欧氏距离等距离度量找到它最相似的 k k k个样本,称为最近的邻居,以这 k k k个样本中数目最多的类别作为新样本的归属类别。
原理分析
先讲一讲用KNN做预测的原理。假定第 i i i个训练样本的 n n n个特征向量为 ( f 1 i , f 2 i , ⋯ , f n i ) (f_1^i,f_2^i,\cdots,f_n^i) (f1i,f2i,⋯,fni),它们对应的 m m m维特征属性目标为 ( t 1 i , t 2 i , ⋯ , t n i ) (t_1^i,t_2^i,\cdots,t_n^i) (t1i,t2i,⋯,tni) 。当给定一个特征向量为 ( q 1 , q 2 , ⋯ , q n ) (q_1,q_2,\cdots,q_n) (q1,q2,⋯,qn) 的新样本时,我们用其特征寻找 k k k 个最相似的训练样本,近邻判定的标准为特征向量之间的欧式距离,新样本与第 i i i个训练样本之间的欧氏距离的计算公式如下:
∑ x = 1 n ( f x i − q x ) 2 \sqrt{\sum_{x=1}^{n}\left(f_{x}^{i}-q_{x}\right)^{2}} x=1∑n(fxi−qx)2
假定找到的 k k k个最近邻训练样本的目标向量分别为 ( t 1 , t 2 , ⋯ , t k ) (t^1,t^2,\cdots,t^k) (t1,t2,⋯,tk) ,以它们的平均值作为需要预测的新样本的目标向量:
∑ i = 1 k t i k \sum_{i=1}^{k} \frac{t^{i}}{k} i=1∑kkti
而KNN在时间序列中的应用方法为,以时间序列数据为目标值,目标值的滞后值为特征值,构造一个类似于自回归的模型。
不断关注在实际发生之前先了解发生了什么,这促使我们继续进行这项研究。我们还将尝试并了解 COVID-19对股票价格的影响。
所需包
library(quantmod) R的定量金融建模和交易框架 library(forecast) 预测时间序列和时间序列模型 library(tseries) 时间序列分析和计算金融。 library(timeseries) 'S4'类和金融时间序列的各种工具。 library(readxl) readxl包使你能够轻松地将数据从Excel中取出并输入R中。 library(kableExtra) 显示表格 library(data.table) 大数据的快速聚合 library(DT) 以更好的方式显示数据 library(tsfknn) 进行KNN回归预测
数据准备
导入数据
我们使用Quantmod软件包获取了Google股票价格2015年1月1日到2020年4月24日的数据,用于我们的分析。为了分析COVID-19对Google股票价格的影响,我们从quantmod数据包中获取了两组数据。
- 首先将其命名为data\_before\_covid,其中包含截至2020年2月28日的数据。
- 第二个名为data\_after\_covid,其中包含截至2020年4月24日的数据。
所有分析和模型都将在两个数据集上进行,以分析COVID-19的影响(如果有)。
getSymbols("GOG" fro= "2015-01-01", to = "2019-02-28")
before_covid <-dafae(GOOG)
getSymbols("GOG" , frm = "2015-01-01")
after_covid <- as.tae(GOOG)
数据的图形表示
par(mfrow = c(1,2)) plot.ts(fore_c)
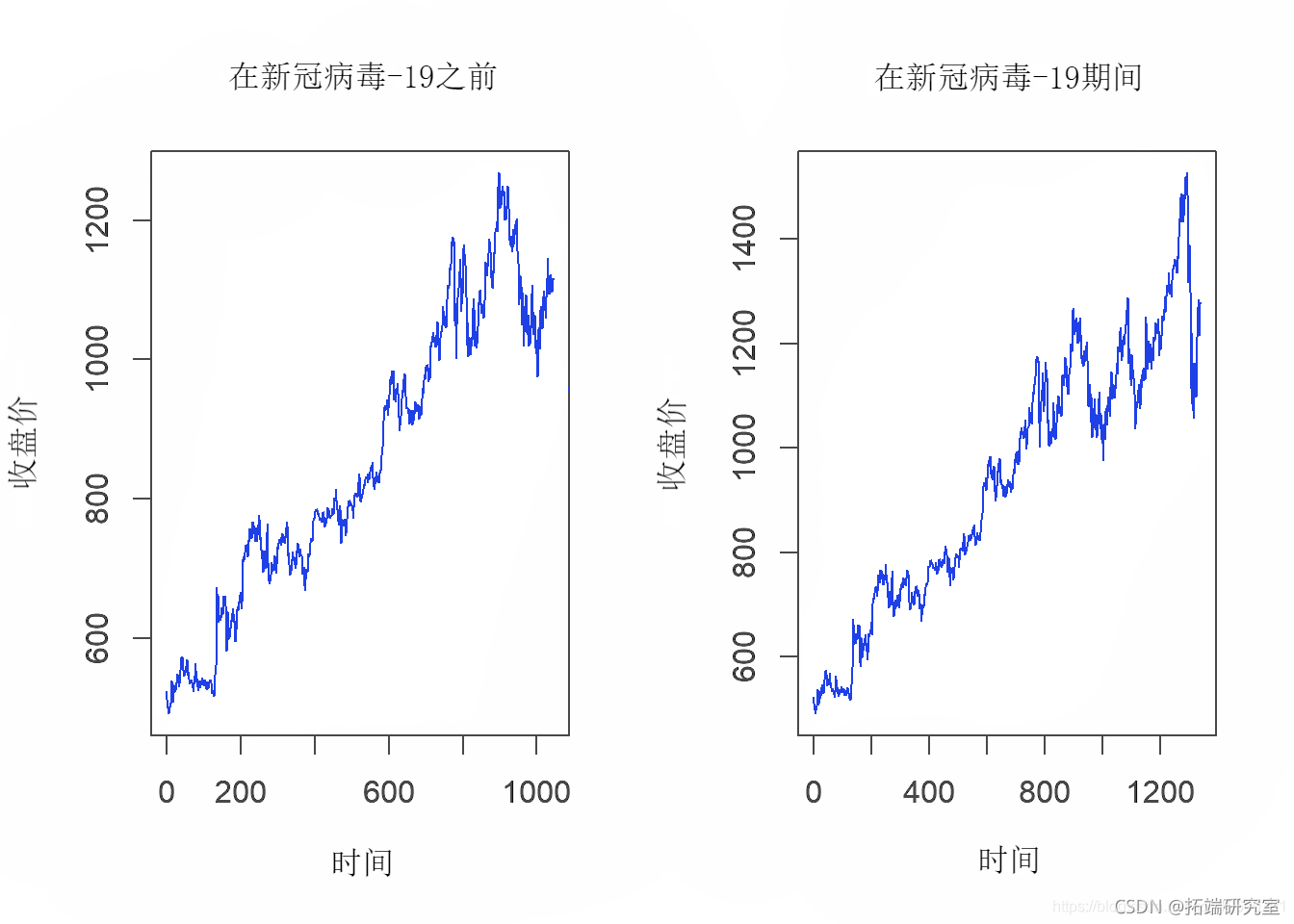
数据集预览
最终数据集可以在下面的交互式表格中找到。
table(before_covid)
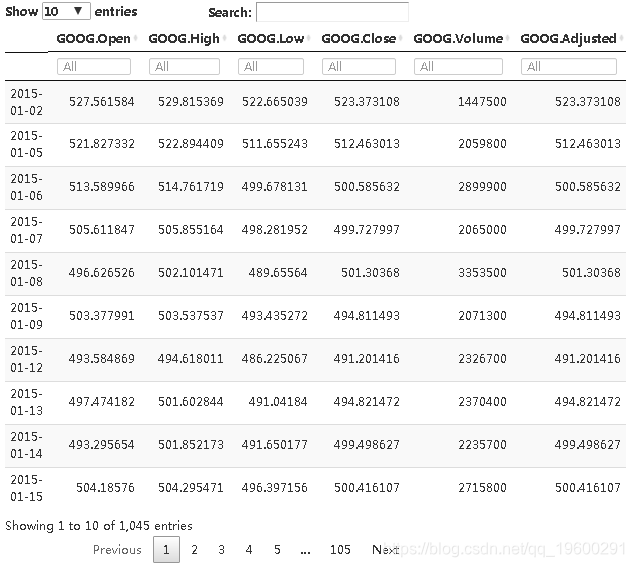
变量汇总
| 变量 | 描述 |
|---|---|
| Open | 当日股票开盘价 |
| High | 当日股票最高价 |
| Low | 当日股价最低 |
| Close | 当日股票收盘价 |
| Volumn | 总交易量 |
| Adjusted | 调整后的股票价格,包括风险或策略 |
ARIMA模型
我们首先分析两个数据集的ACF和PACF图。
par(mfrow = c(2,2)) acft(bfoe_covid) pacf(bfre_covid)
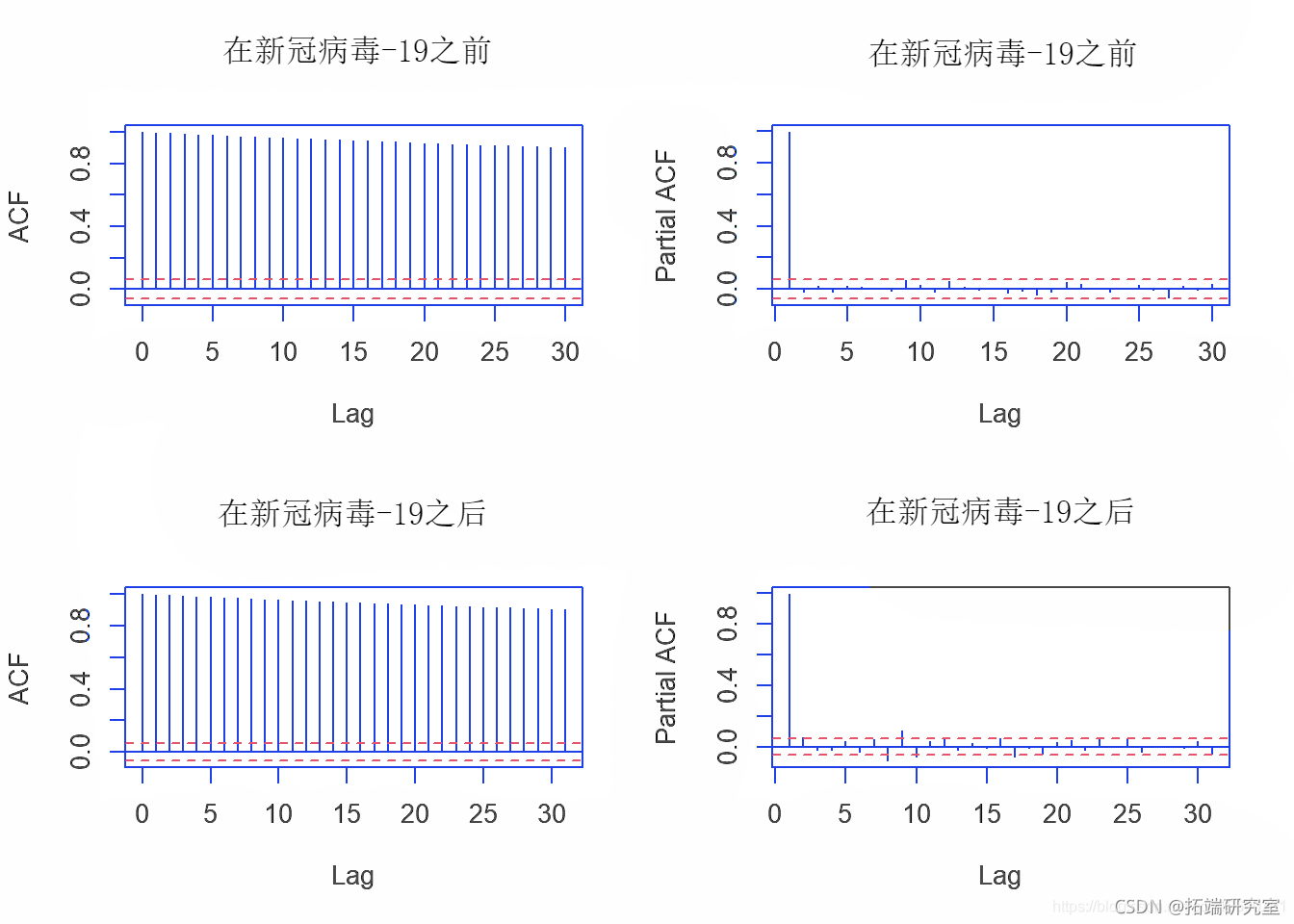
然后,我们进行 ADF(Dickey-Fuller) 检验和 KPSS(Kwiatkowski-Phillips-Schmidt-Shin) 检验,检验两个数据集收盘价的时间序列数据的平稳性。
print(adf.test)

随时关注您喜欢的主题
print(adfes(sata\_after\_covid))

通过以上ADF检验,我们可以得出以下结论:
- 对于COVID-19之前的数据集,ADF检验给出的p值为 0.2093,该值大于0.05,因此说明时间序列数据 不是平稳的。
- 对于COVID-19之后的数据集,ADF检验给出的p值为0.01974,该值 小于0.05,这说明时间序列数据是 平稳的。
print(kpss.s(t\_before\_covid))

print(kpss.est(Dafter_covid))

通过以上KPSS检验,我们可以得出以下结论:
- 对于COVID-19之前的数据集,KPSS检验得出的p值为 0.01,该值小于0.05,因此说明时间序列数据 不是平稳的。
- 对于COVID-19之后的数据集,KPSS检验给出的p值为 0.01,该值小于0.05,这说明时间序列数据 不是平稳的。
因此,我们可以从以上检验得出结论,时间序列数据 不是平稳的。
然后,我们使用 auto 函数来确定每个数据集的时间序列模型。
auto.ar(befor_covid, lamd = "auto")
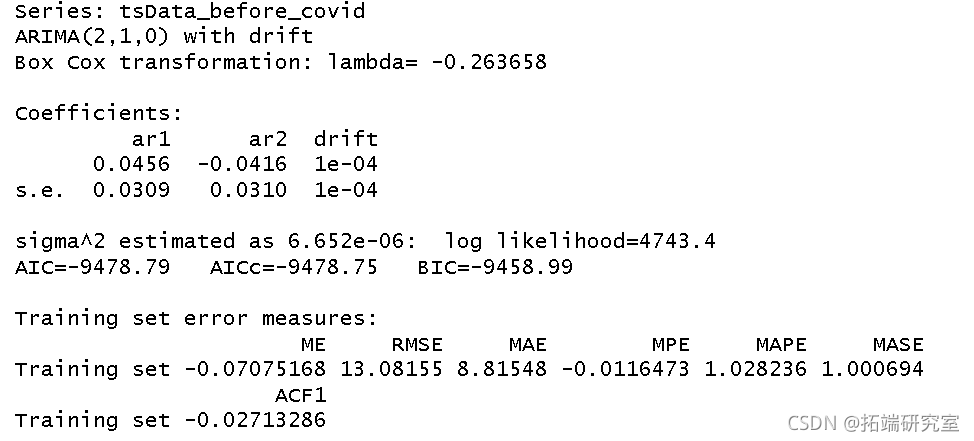
获得模型后,我们将对每个拟合模型执行残差诊断。
auto.arma(after_covid)
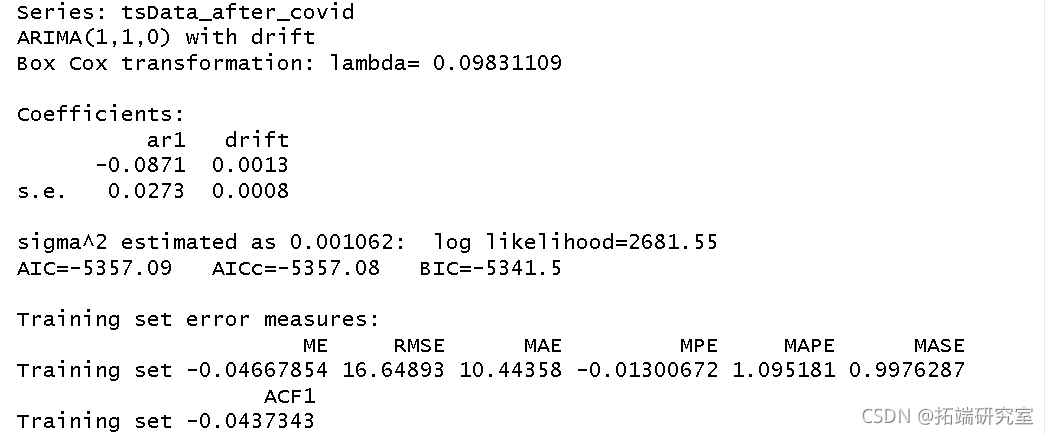
从auto函数中,我们得出两个数据集的以下模型:
- 在COVID-19之前:ARIMA(2,1,0)
- 在COVID-19之后:ARIMA(1,1,1)
par(mfrow = c(2,3)) plot(before_covidresiduals) plot(mfter_covidresiduals)
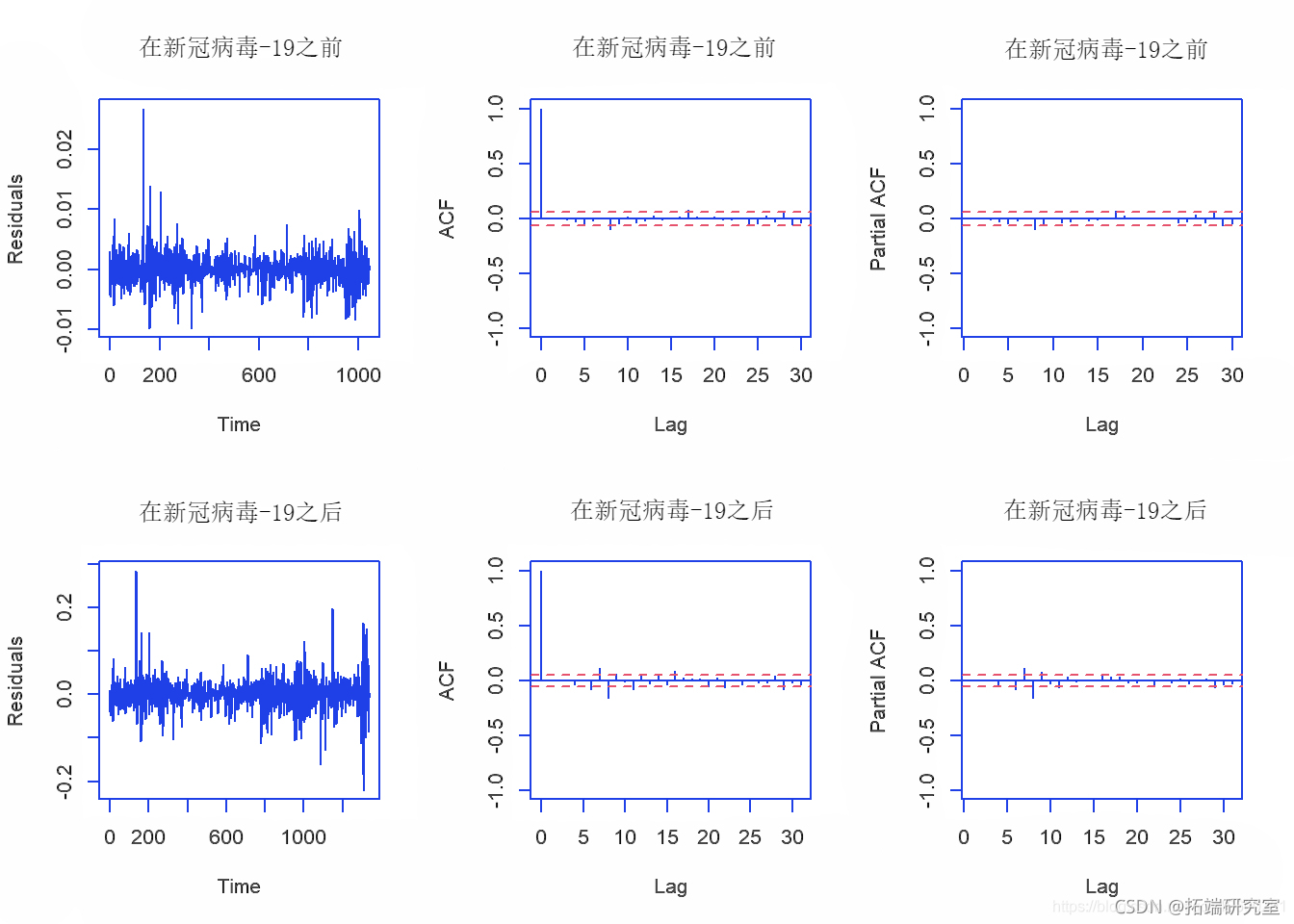
从残差图中,我们可以确认残差的平均值为0,并且方差也为常数。对于滞后> 0,ACF为0,而PACF也为0。
因此,我们可以说残差表现得像白噪声,并得出结论:ARIMA(2,1,0)和ARIMA(1,1,1)模型很好地拟合了数据。或者,我们也可以使用Box-Ljung检验在0.05的显着性水平上进行检验残差是符合白噪声。
Box.test(moderesiduals)

Box.tst(moeit\_fter\_covidreia, type = "Ljung-Box")

在此,两个模型的p值均大于0.05。因此,在显着性水平为0.05的情况下,我们无法拒绝原假设,而得出的结论是残差遵循白噪声。这意味着该模型很好地拟合了数据。
一旦为每个数据集确定了模型,就可以预测未来几天的股票价格。
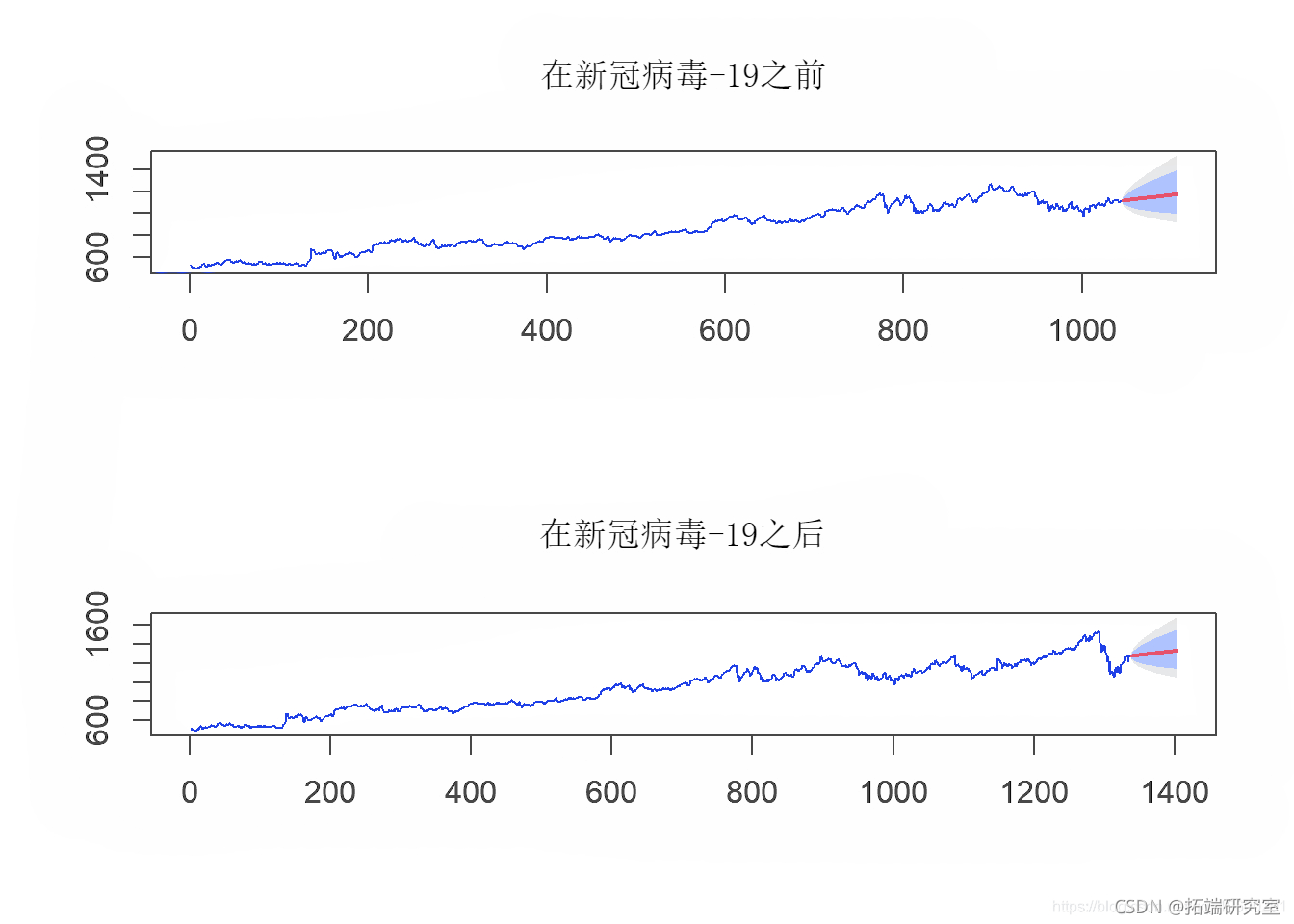
KNN回归时间序列预测模型
KNN模型可用于分类和回归问题。最受欢迎的应用是将其用于分类问题。现在,使用r软件包,可以在任何回归任务应用KNN。这项研究的目的是说明不同的预测工具,对其进行比较并分析预测的行为。在我们的KNN研究之后,我们提出可以将其用于分类和回归问题。为了预测新数据点的值,模型使用“特征相似度”,根据新点与训练集上点的相似程度为值分配新点。
第一项任务是确定我们的KNN模型中的k值。选择k值的一般经验法则是取样本中数据点数的平方根。因此,对于COVID-19之前的数据集,我们取k = 32;对于COVID-19之后的数据集,我们取k = 36。
par(mfrow = c(2,1)) knn\_before\_covid <- kn(bfrvdGO.Clse, k = 32) knn\_after\_covid <- kn(ber_oiGOG.lose ,k = 36) plot(knn\_before\_covid ) plot(knn\_after\_covid )
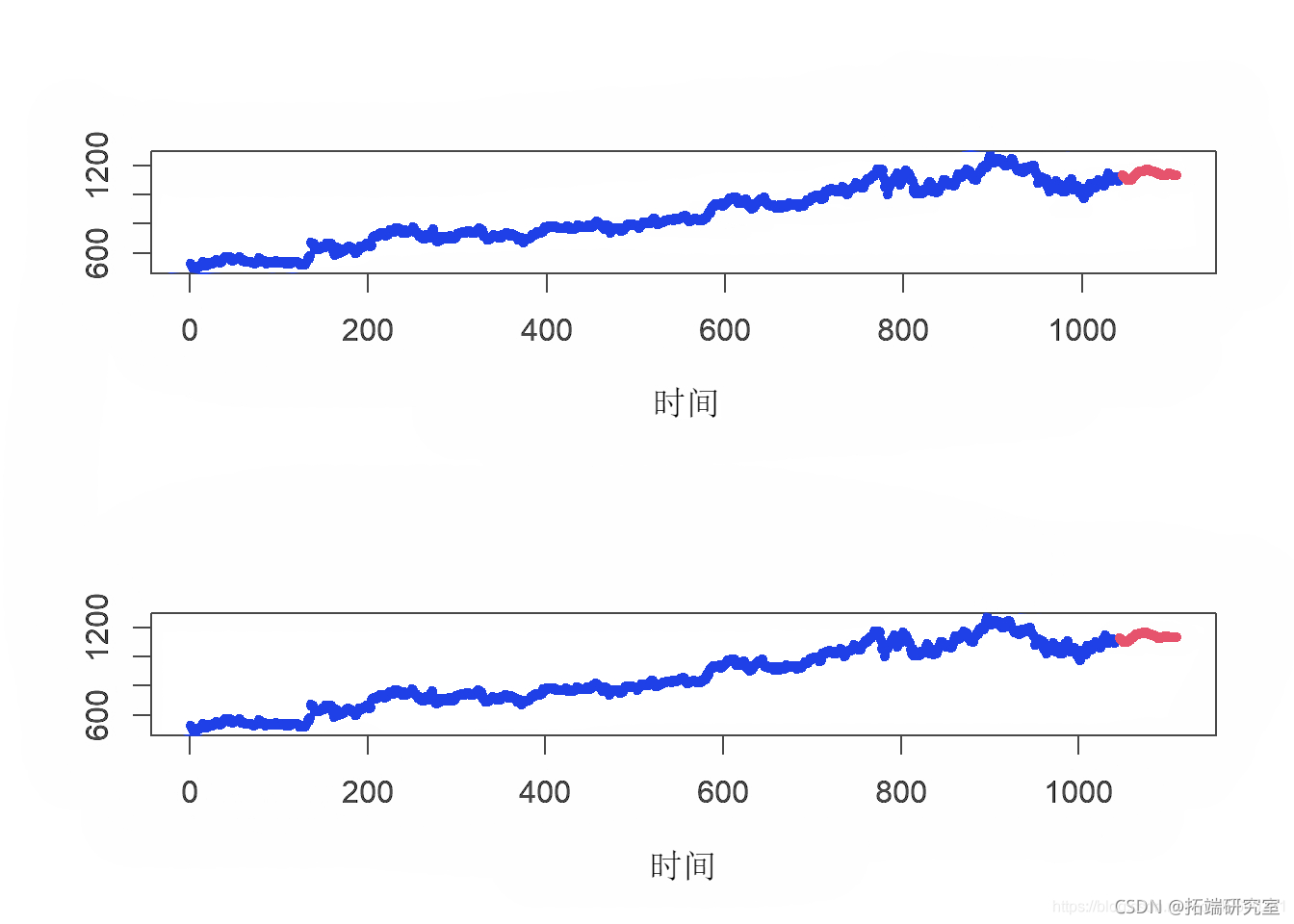
然后,我们针对预测时间序列评估KNN模型。
before\_cvid <- ll\_ig(pdn\_befr\_vid) afer\_vd<- rog\_ogn(redkn\_afer\_vd)

前馈神经网络建模
我们将尝试实现的下一个模型是带有神经网络的预测模型。在此模型中,我们使用单个隐藏层形式,其中只有一层输入节点将加权输入发送到接收节点的下一层。预测函数将单个隐藏层神经网络模型拟合到时间序列。函数模型方法是将时间序列的滞后值用作输入数据,以达到非线性自回归模型。
第一步是确定神经网络的隐藏层数。尽管没有用于计算隐藏层数的特定方法,但时间序列预测遵循的最常见方法是通过计算使用以下公式:
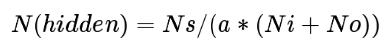
其中Ns:训练样本数Ni:输入神经元数No:输出神经元数a:1.5 ^ -10
#隐藏层的创建 hn\_before\_covid <- length(before.Close)/(alpha*(lengthGOOG.Close + 61) hn\_after\_covid <- length(after\_covidClose)/(alpha*(lengthafter\_ovdClose+65)) #拟合nn nn(before\_covid$GOOG.Close, size = hn\_beoe_cid, # 使用nnetar进行预测。 forecast(befe_cvid, h 61, I =UE) forecast(aftr_coid, h = 5, I = RE)
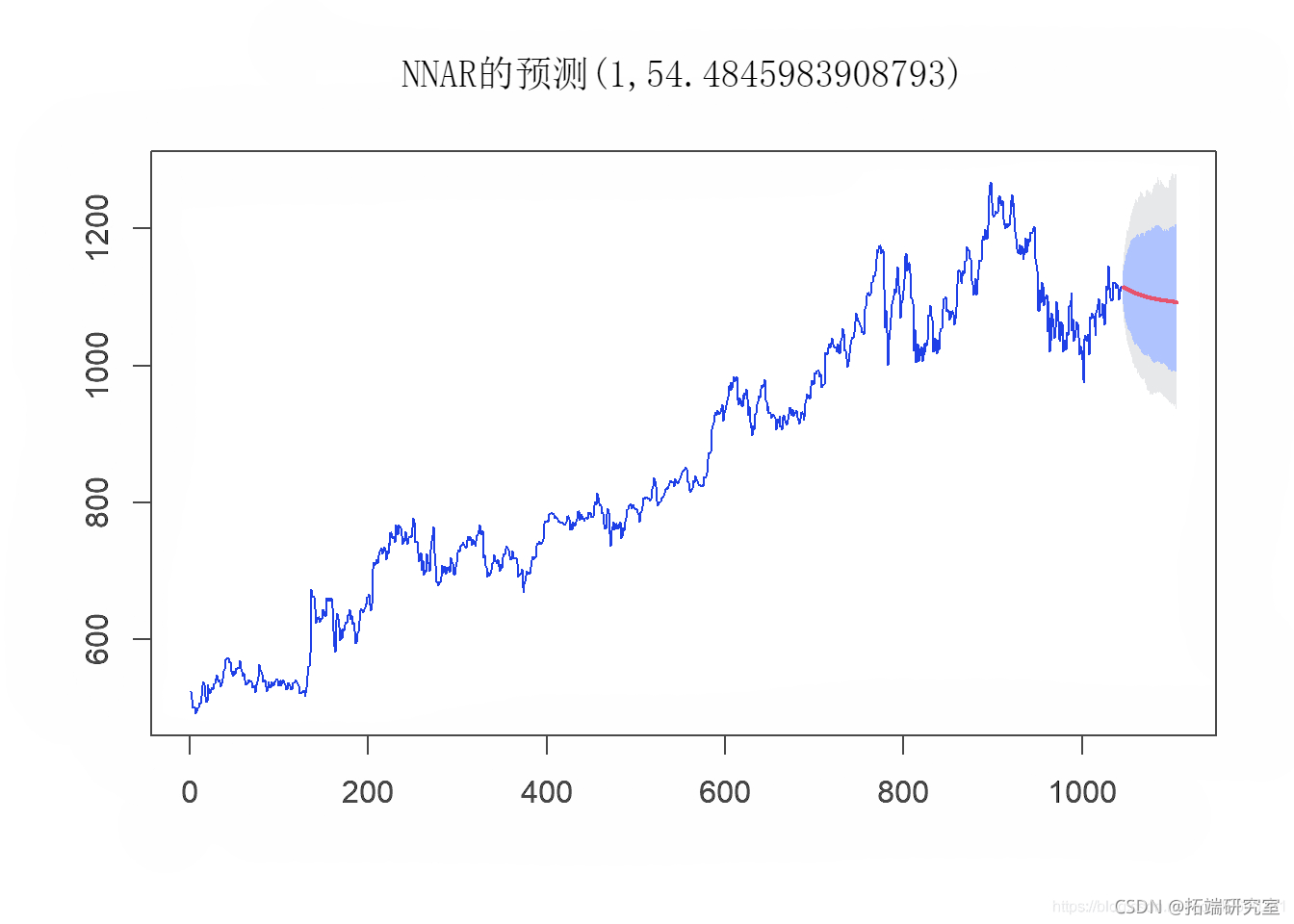
plot(nn\_fcst\_afte_cvid)
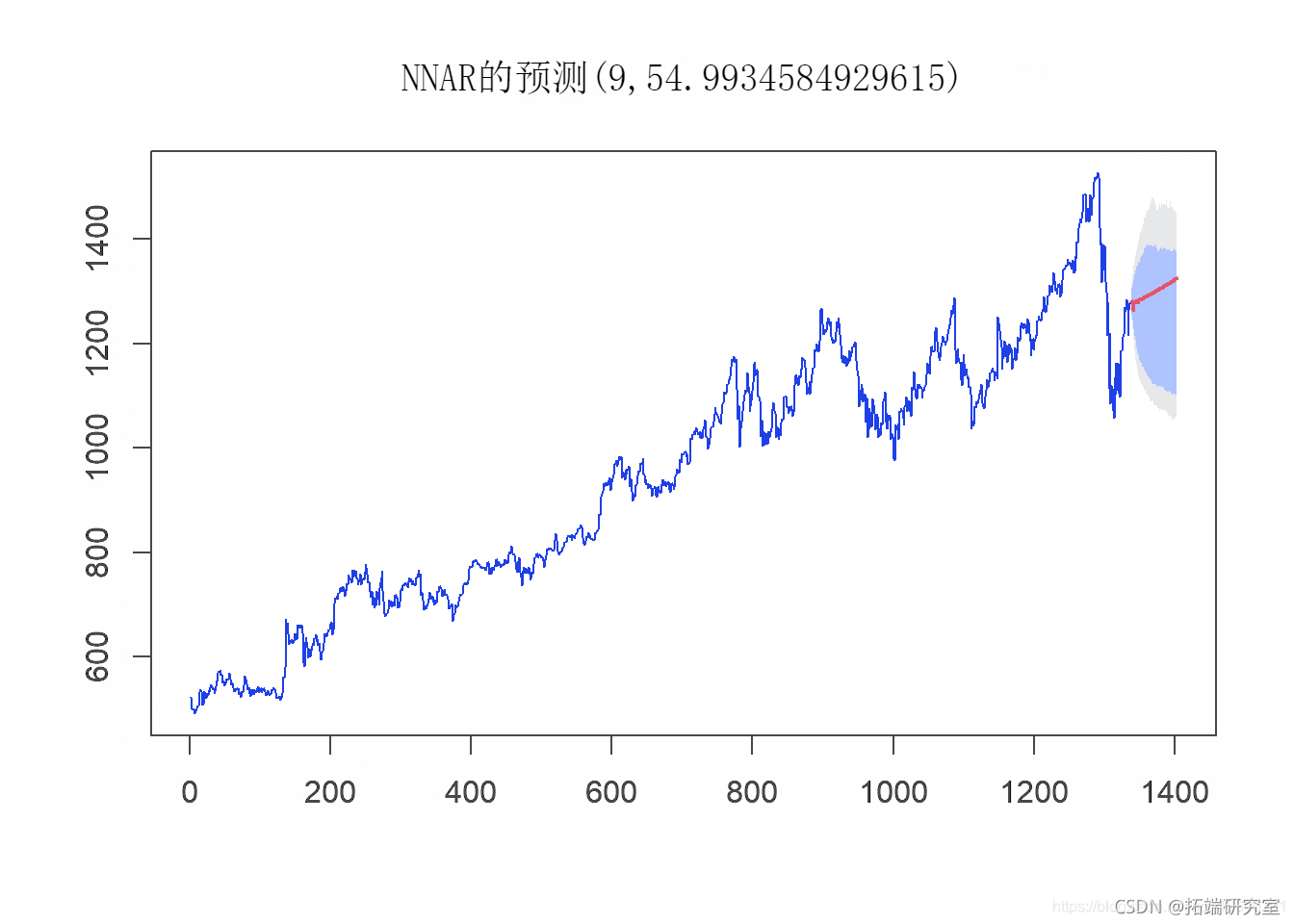
然后,我们使用以下参数分析神经网络模型的性能:
accuracy

accuracy

所有模型的比较
现在,我们使用参数诸如RMSE(均方根误差),MAE(均值绝对误差)和MAPE(均值绝对百分比误差)对所有三个模型进行分析 。
sumary\_le\_efore_oid <- data.frame(RMSE = nuerc(), MAE = uer(), MAPE = numric(), snsAsacrs = FALSE) summ\_tabe\_fter_ovd <- data.fame(RMSE = umeri(), MAE = nmei(), MAPE = numeic()) kable(smary\_abe\_eor_oid )
COVID-19之前的数据模型汇总
| 模型 | RMSE | MAE | MAPE |
|---|---|---|---|
| ARIMA | 13.0 | 8.8 | 1.0 |
| KNN | 44.0 | 33.7 | 3.1 |
| 神经网络 | 13.0 | 8.7 | 1.0 |
kable(sumary\_tbl\_aft_ci fulith = F, fixdtead = T )
COVID-19之后的数据模型汇总
| 模型 | RMSE | MAE | MAPE |
|---|---|---|---|
| ARIMA | 16.6 | 10.4 | 1.0 |
| KNN | 45.9 | 35.7 | 3.3 |
| 神经网络 | 14.7 | 9.8 | 1.0 |
因此,从以上模型性能参数的总结中,我们可以看到神经网络模型在两个数据集上的性能均优于ARIMA和KNN模型。因此,我们将使用神经网络模型来预测未来两个月的股价。
最终模型:COVID-19之前
现在,我们使用直到2月的数据来预测3月和4月的值,然后将预测价格与实际价格进行比较,以检查是否由于COVID-19可以归因于任何重大影响。
foestdungcvid<- datafame("De
"Actua Values" =
datatable(foestdungcvid, ilte= 'to')
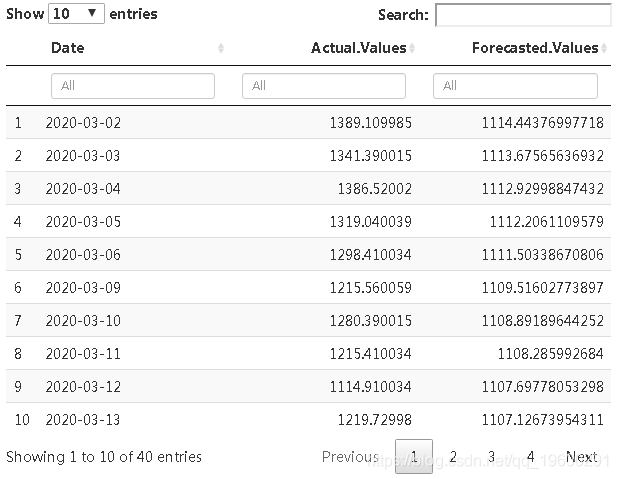
从表中我们可以看到,3月和4月期间,Google股票的实际价值通常比预测值要高一些。因此,可以说,尽管发生了这种全球性大流行,但Google股票的表现仍然相当不错。
最终模型:COVID-19之后
现在,我们使用直到4月的数据预测5月和6月的值,以了解Google的未来股价。
foreataov <- data.frae(dn_reataeimean ) table(foreataov )
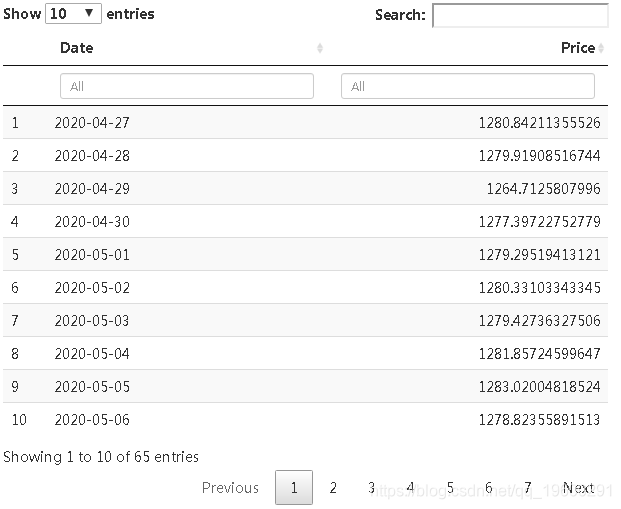
从表中可以得出结论,在5月和6月的接下来的几个月中,Google股票的价格将继续上涨并表现良好。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 SPSS与Python用Resblock优化BP神经网络分析慢性胃炎病历数据聚类K-means/AGNES、关联规则挖掘及预测
SPSS与Python用Resblock优化BP神经网络分析慢性胃炎病历数据聚类K-means/AGNES、关联规则挖掘及预测 Python、Flask、ECharts及MySQL疫情数据可视化系统设计与实现——多模块联动实时展示优化|附代码数据
Python、Flask、ECharts及MySQL疫情数据可视化系统设计与实现——多模块联动实时展示优化|附代码数据 Python用Ridge、Lasso、KNN、SVM、决策树、随机森林、XGBoost共享单车数据集需求预测及动态资源调配策略优化|附代码数据
Python用Ridge、Lasso、KNN、SVM、决策树、随机森林、XGBoost共享单车数据集需求预测及动态资源调配策略优化|附代码数据



