在本文中，我们使用了逻辑回归、决策树和随机森林模型来对信用数据集进行分类预测。
最近我们被客户要求撰写关于信用数据的研究报告，包括一些图形和统计输出。在本文中，我们使用了逻辑回归、决策树和随机森林模型来对信用数据集进行分类预测并比较了它们的性能。
数据集是
credit=read.csv("german_credit.csv", header = TRUE, sep = ",")看起来所有变量都是数字变量，但实际上，大多数都是因子变量，
> str(credit)
'data.frame': 1000 obs. of 21 variables:
$ Creditability : int 1 1 1 1 1 1 1 1 1 1 ...
$ Account.Balance : int 1 1 2 1 1 1 1 1 4 2 ...
$ Duration : int 18 9 12 12 12 10 8 ...
$ Purpose : int 2 0 9 0 0 0 0 0 3 3 ...Step 1 数据准备
– 积累一个足够大的数据样本，且每个样本有足够的特征数。比如需要100个借款人的10个特征（年龄、性别等）。需要充分考虑到样本的时效性和代表性。
– 那么多大才为”足够大“？应该说，没有一个放之天下皆准的答案，取决于数据质量、模型复杂性等等。
来自Google工程师的说，想知道要多少数据才够建模，得建个模型跑跑才知道：How-much-training-data-do-you-need（他建模得出的结论是，一个优秀的性能模型需要训练数据的数量10倍于该模型中参数的数量。）
– 界定这些数据样本的观察期和表现期。观察期是指在设定的观察日之前的一段时间，表现期是指客户观察日之后的一段时间。对于信用评分而言，需要用观察期内申请人的信用历史及表现（X），以及表现期内申请人的还款表现（Y），通过模型拟合出X与Y之间的关系。
Step 2 数据处理
从生产环境导出的数据往往并不完美，有大量影响分析的缺失值和异常值。我们需要剔除缺失率太高的变量，剔除按业务逻辑完全不可解释的变量等等。这是一个听起来很简单但实际上需要耗费大量精力的过程，会极大影响到模型准确性。
Step 3 变量分析
– 单变量分析，如应用统计学方法筛选出预测能力较高的变量，获取自变量中对违约状态影响最显著的指标。经过筛选的变量将进入信用评分模型。再比如需要分析变量的分布是否大致呈正态分布，才能够满足后续分析的条件。
– 变量之间相关性的分析，如两两之间的相关性、VIF多重共线性。如果变量之间相关性显著，会影响模型的预测效果。
“在数据分析和模型开发中，数据集合往往包含着几百上千个潜在的、具有预测力的变量……许多变量之间往往存在高度的相关性、反映潜在的共同的信息维度。选择代表变量的标准是该变量与其所属的信息维度尽可能的高度相关，而与其他信息维度尽可能的低度相关。”
——《信用评分模型技术与应用》
Step 4 评分卡构建
现在我们已经拥有了一些非常“优秀”的变量，那我们怎么利用这些变量得到我们所需要的答案呢？这是一个已知X求Y的问题，我们需要选择一个合适的模型方法去解决和预测。常见的模型方法有线性回归、非线性回归分析、决策树等等。
逻辑回归是在信用评分卡开发中非常有代表性的模型方法。在这个模型中，经过上述筛选的每一个变量会进行证据权重转换，逻辑回归可以将我们所熟知的借款人特征转化为一个标准的评分卡，当我们输入这些变量的具体值的时候，可以得到相应的分数。
让我们将分类变量转换为因子变量，
> F=c(1,2,4,5,7,8,9,10,11,12,13,15,16,17,18,19,20)
> for(i in F) credit[,i]=as.factor(credit[,i])现在让我们创建比例为1：2 的训练和测试数据集
视频
从决策树到随机森林：R语言信用卡违约分析信贷数据实例
视频
逻辑回归Logistic模型原理和R语言分类预测冠心病风险实例
> i_test=sample(1:nrow(credit),size=333)
> i_calibration=(1:nrow(credit))[-i_test]我们可以拟合的第一个模型是对选定协变量的逻辑回归
> LogisticModel <- glm(Creditability ~ Account.Balance + Payment.Status.of.Previous.Credit + Purpose +
Length.of.current.employment +
Sex...Marital.Status, family=binomia基于该模型，可以绘制ROC曲线并计算AUC（在新的验证数据集上）
> AUCLog1=performance(pred, measure = "auc")@y.values[[1]]
> cat("AUC: ",AUCLog1,"\n")
AUC: 0.7340997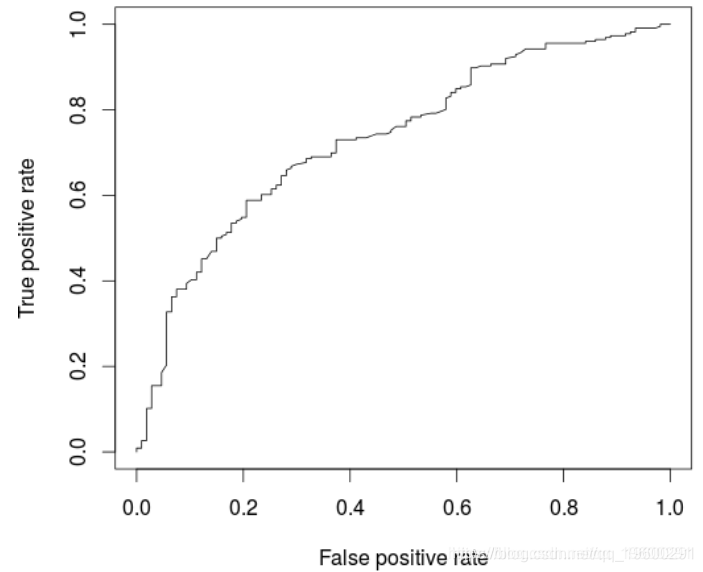
一种替代方法是考虑所有解释变量的逻辑回归
glm(Creditability ~ .,
+ family=binomial,
+ data = credit[i_calibrat我们可能在这里过拟合，可以在ROC曲线上观察到
> perf <- performance(pred, "tpr", "fpr
> AUCLog2=performance(pred, measure = "auc")@y.values[[1]]
> cat("AUC: ",AUCLog2,"\n")
AUC: 0.7609792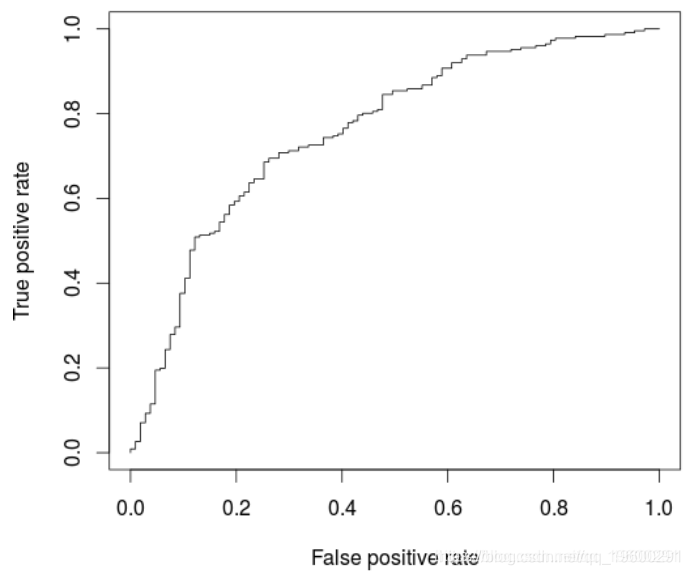
与以前的模型相比，此处略有改善，后者仅考虑了五个解释变量。
现在考虑回归树模型（在所有协变量上）
我们可以使用
> prp(ArbreModel,type=2,extra=1)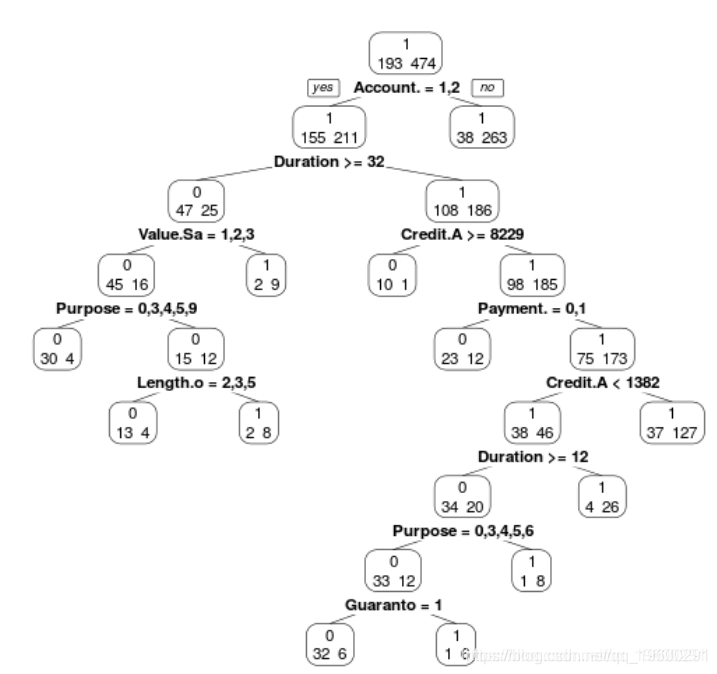
模型的ROC曲线为
(pred, "tpr", "fpr")
> plot(perf)
> cat("AUC: ",AUCArbre,"\n")
AUC: 0.7100323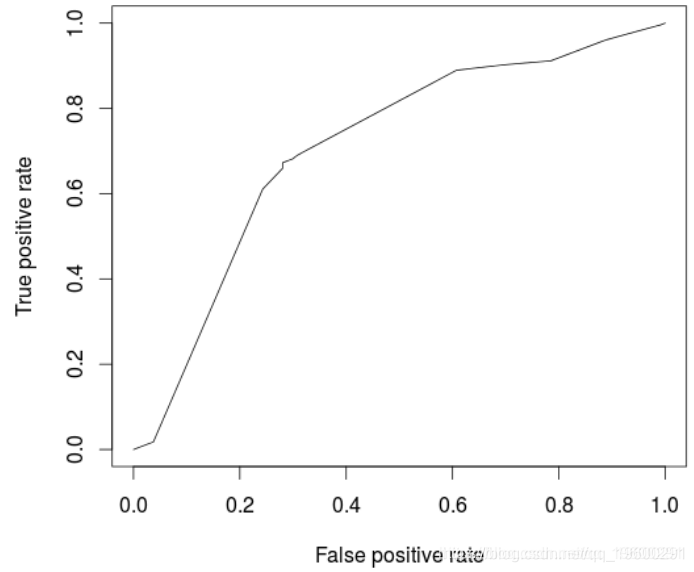
不出所料，与逻辑回归相比，模型性能较低。一个自然的想法是使用随机森林优化。
> library(randomForest)
> RF <- randomForest(Creditability ~ .,
+ data = credit[i_calibration,])
> fitForet <- predict(RF,
> cat("AUC: ",AUCRF,"\n")
AUC: 0.7682367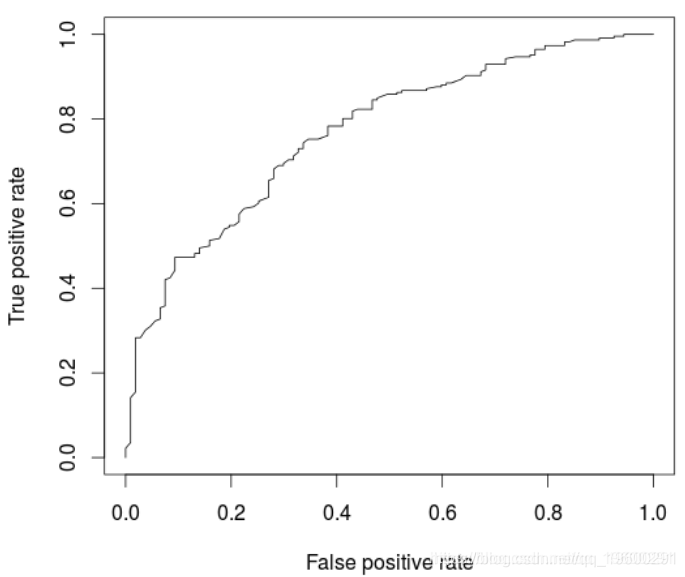
在这里，该模型（略）优于逻辑回归。实际上，如果我们创建很多训练/验证样本并比较AUC，平均而言，随机森林的表现要比逻辑回归好，
> AUCfun=function(i){
+ set.seed(i)
+ i_test=sample(1:nrow(credit),size=333)
+ i_calibration=(1:nrow(credit))[-i_test]
+ summary(LogisticModel)
+ fitLog <- predict(LogisticModel,type="response",
+ newdata=credit[i_test,])
+ library(ROCR)
+ pred = prediction( fitLog, credit$Creditability[i_test])
+ RF <- randomForest(Creditability ~ .,
+ data = credit[i_calibration,])
+ pred = prediction( fitForet, credit$Creditability[i_test])
+ return(c(AUCLog2,AUCRF))
+ }
> plot(t(A))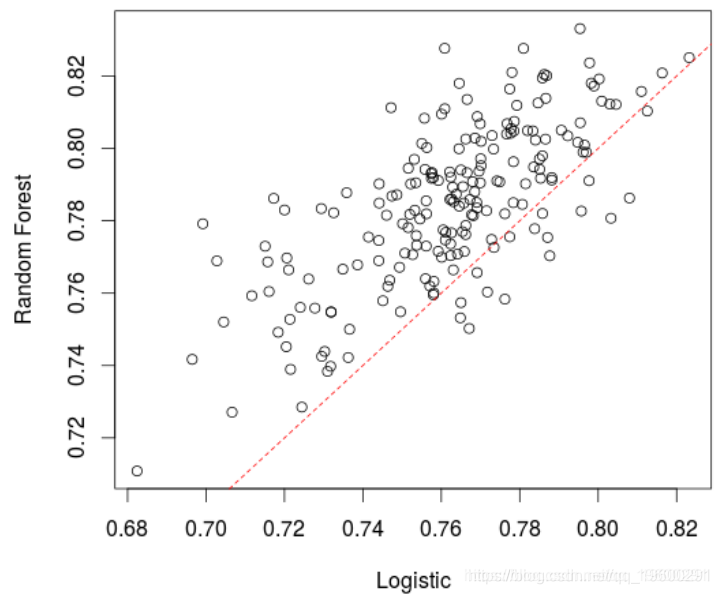
Python古代文物成分分析与鉴别研究：灰色关联度、岭回归、K-means聚类、决策树分析
Python酒店预订数据：随机森林与逻辑回归模型ROC曲线可视化
视频讲解|Python图神经网络GNN原理与应用探索交通数据预测
