在最近的一篇文章中,我们展示了一个LSTM模型,通过假近邻(FNN)损失进行正则化,可以用来重建一个非线性动态系统。
在这里,我们探讨了同样的技术是如何协助预测的。与 “普通LSTM “相比,FNN-LSTM在数据集上提高了性能,特别是在多步骤预测的初始阶段。
深度学习与时间序列的结合:生成经验性时间序列数据的预测。
LSTM(Long-short time memory,LSTM)模型,亦即是长段时间模型。LSTM的原理这篇博客讲的十分的清楚,建议英语好的小伙伴直接去看原文,我这里就大致的翻译精简一下。
人类天生具备的一个能力就是记忆的持久性,可以根据过往经验,从而推断出当前看到的内容的实际含义。如看电影的时候可以通过先前时间去推断后续事件;看一篇文章的时候,同样可以通过过往的知识积累去推断文章中每个词语的含义。而传统的神经网络并没有“持久性”,每一个神经元不能通过前面神经元的结果进行推断,为了解决这一问题科学家提出了递归神经网络(Recurrent Neural Networks,RNN)。RNN是包含循环的神经网络(如图所示),允许信息的持久化。其中A可以看作神经网络的一个缩影,接受某时刻的输入X t 然后输出对应的结果h t ,一个回路可以允许信息从一步传递到另一步。
简而言之,解决的问题如下。对一个已知或假定为非线性且高度依赖初始条件的系统进行观测,得出一系列标量的测量结果。这些测量结果不仅仅有噪声,而且,它们是多维状态空间对一条线的投影。
通常在非线性时间序列分析中,这种标量系列的观测值是通过在每个时间点上补充同一系列的滞后测量值来增加的–这种技术称为滞后坐标嵌入(Sauer, Yorke, and Casdagli 1991)。例如,我们可以有一个由向量X1、X2和X3组成的矩阵,而不是只有一个向量X1,X2包含与X1相同的值,但从第三个观测点开始,而X3则从第五个观测点开始。在这种情况下,滞后将是2,而嵌入维度是3。各种定理指出,如果这些参数被充分选择,就有可能重建完整的状态空间。但是有一个问题。这些定理假定真实状态空间的维度是已知的,而在许多现实世界的应用中,情况并非如此。
训练一个自动编码器,它的中间表示法封装了系统的吸引子。但不是任何MSE优化的自动编码器。潜在表征通过假近邻(FNN)损失进行规范化,这是一种常用于延迟坐标嵌入的技术,以确定适当的嵌入维度。假近邻是指那些在n维空间中接近,但在n+1维空间中明显相距较远的样本。
我们首先描述设置,包括模型定义、训练程序和数据准备。
设置
从重建到预测
像通常的自动编码器一样,训练时的目标与输入相同,这意味着整体损失由两部分组成。FNN损失,仅在潜像上计算,以及输入和输出之间的均方误差损失。现在,对于预测来说,目标由未来的值组成,只要我们想预测,就有很多。换句话说。架构保持不变,但我们以标准的RNN方式进行预测,而不是重建。通常的RNN设置只是直接连接所需数量的LSTM,我们有一个LSTM编码器,输出一个(无时间步长的)潜在代码,和一个LSTM解码器,从该代码开始,根据需要重复多次,预测所需数量的未来值。
这当然意味着,为了评估预测性能,我们需要与仅有LSTM设置的模型进行比较。这
我们在四个数据集上进行这些比较。
模型定义和训练设置
在所有四个实验中,我们使用相同的模型定义和训练程序,唯一不同的参数是LSTMs中使用的时间步数。
两种架构都简单明了,并且在参数数量上具有可比性–基本上都是由两个具有32个单元的LSTM组成(所有实验中n_recurrent将被设置为32)。
FNN-LSTM
我们把编码器LSTM分成了两个,最大潜在状态维度保持为10。
# DL-相关软件包
library(tensorflow)
library(keras)
keras_custom(name = ne,) {
self$noe <- layer_gausise(stddev = 0.5)
selfst <- layelstm(
units = nrecent,
input\_se = c(n\_times, n_features),
return_seces = TRUE
)
self$bm1 <- layer_bation()
self$l2 <- lstm(
uni = n_le,
return_= FALSE
)
self$bato<- layer_batcn()
latent <- 10L
features <- 1
hidden <- 32
正则器,FNN损失,没有变化。
lossnn <- function(x) {
# 改变这些参数就相当于
# 改变正则器的强度,所以我们保持这些参数固定(这些值
#对应于Kennel等人1992年使用的原始值)。)
rtol <- 10
atol <- 2
k_frac <- 0.01
k <- max(1, floor(k\_frac * batch\_size))
##距离矩阵计算的矢量版本
tri_mask <-
tf$linalg$band_part(
tf$ones(
shape
dtype
),
num_lower = -1L,
num_upper = 0L
)
# 潜在的x batch_size x 1
x_squared <-
tf$reduce\_sum(batch\_masked * batch_masked,
axis = 2L,
keepdims = TRUE)
#(latent, batch\_size, batch\_size)
all\_dists <- pdist\_vector
# 避免在有零的情况下出现奇异现象
#(latent, batch\_size, batch\_size)
all_dists <-
tf$clip\_by\_value(all\_dists, 1e-14, tf$reduce\_max(all_dists))
# L2正则化
activations\_batch\_averaged <-
sqrt(ce_mean(tf$square(x), axis = 0L))
loss <-reduce\_sum(multiply(reg\_weights, acti\_batch\_averaged))
损失
训练也没有变化,只是现在除了损失之外,我们还不断地输出潜变量的变异。这是因为在FNN-LSTM中,我们必须为FNN的损失部分选择一个适当的权重。一个 “适当的权重 “是指在前n个变量之后方差急剧下降,n被认为与吸引子维度相对应。这些方差是这样的。

如果我们把方差作为重要性的一个指标,前两个变量显然比其他变量更重要。例如,相关维度被估计为位于2.05左右(Grassberger和Procaccia 1983)。
因此,在这里我们按照常规训练。
code <- encoder(batch\[\[1\]\] )
l\_mse <- mse\_loss(batch\[\[2\]\], prediction)
l\_fnn <- loss\_false_nn(code)
loss<- l\_mse + fnn\_weight * l_fnn
decoder\_gradients, decoder$trainable\_variables
tf$print("损失: ", train_loss$result()
tf$print("MSE: ", train_mse$result()
tf$print("FNN损失。", train_fnn$result())
# 学习率可能也需要调整
optimizer <- optimizer_adam(lr = 1-3)
随时关注您喜欢的主题
我们将用什么作为比较的基线?
VANILLA LSTM
这里是vanilla LSTM,堆叠两个层,每个层的大小也是32。每个数据集都单独选择了丢弃Dropout 和递归丢弃Dropout ,学习率也是如此。
lstm( dropout = 0.2, recurrent_dropout = 0.2)
数据准备
对于所有的实验,数据是以同样的方式准备的。
这里是第一个数据集–间歇泉的数据准备代码–所有其他的数据集都以同样的方式处理。
# 标准化
geyser <- scale(geyser)
# 每个数据集的情况不同
n_timesteps <- 60
batch_size <- 32
# 转化为RNN所需的\[batch_size, timesteps, features\]格式
purrr::map(seq_along(x),
function(i) {
start <- i
end <- i + n_time - 1
out <- x\[start:end\]
出
})
) %>%
na.omit()
}
# 分成输入和目标
x\_train <- train\[, 1:n\_time , ,\]
y\_train <- train\[, (n\_time + 1):(2*n_time ), , \]
# 创建 tfdatasets
slices(list(x\_train, y\_train)) %>%
shuffle(nrow(x_train)) %>%
现在我们准备看看在我们的四个数据集上如何进行预测。
实验
间歇泉数据集
从事时间序列分析工作的人可能听说过Old Faithful,这是一个间歇泉,自2004年以来,每隔44分钟至2小时就会持续喷发。
就像我们上面说的,geyser.csv是这些测量结果的一个子集,包括前10000个数据点。为了给LSTM选择一个适当的时间步长,我们以不同的分辨率检查这个系列。
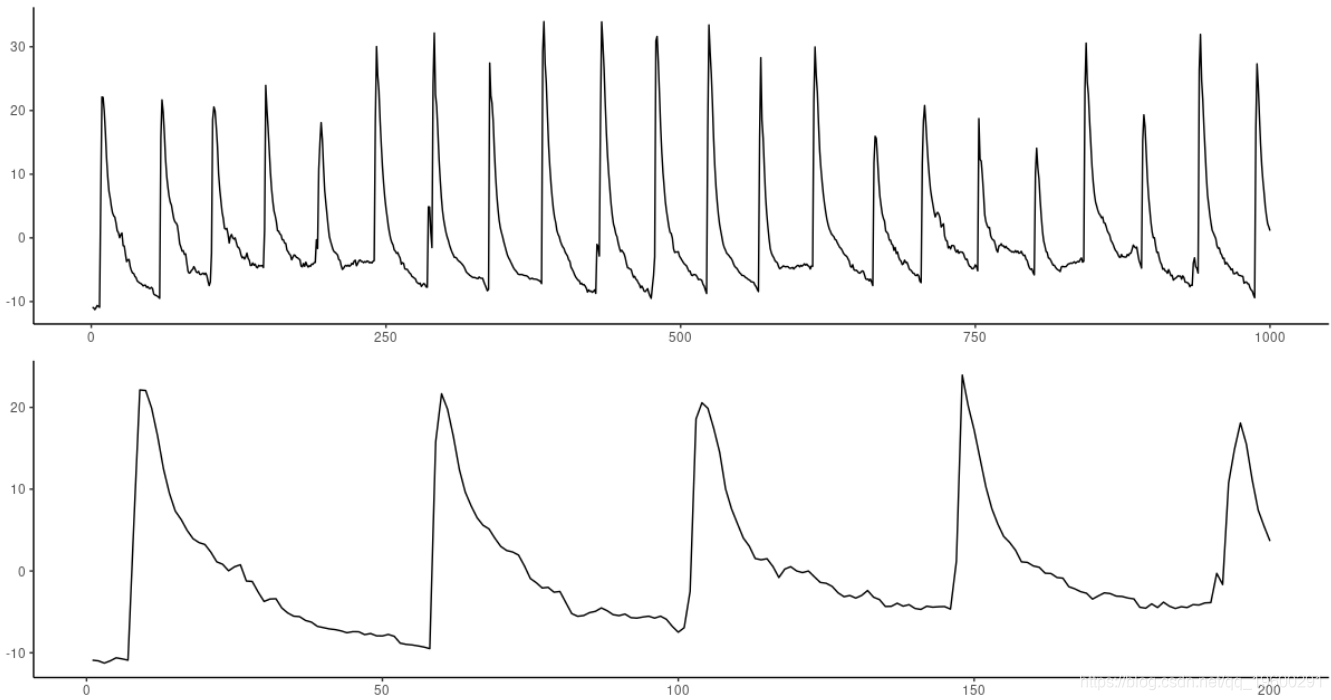
图1:Geyer数据集。顶部:前1000个观测值。底部:放大前200个。
看起来行为是周期性的,周期约为40-50;因此,60个时间步长似乎是个不错的尝试。
在训练了FNN-LSTM和vanilla LSTM 200次后,我们首先检查了测试集上潜变量的方差。这次运行对应的fnn_multiplier的值是0.7。
现在,比较两个模型的预测误差是很有意思。
coded %>% summarise_all(var)

前两个变量和其他变量之间的重要性有所下降;V1和V2的方差也有一个数量级的差异。
以下是用于计算两个模型的每时间段预测误差的代码。同样的代码将用于所有其他数据集。
mse\_fnn <- get\_mse(te\_batch, prediion\_fnn) mse\_lstm <- get\_mse(tesbatch, prediion_lstm) ggplot(mses, aes(step, mse, color = type)) + geom_point() + theme_classic() + theme(legend.position = "none")
而这里是实际的比较。可以看到FNN-LSTM的预测误差在初始时间段明显较低,首先是最开始的预测,从这张图上看,我们发现它是相当不错的!
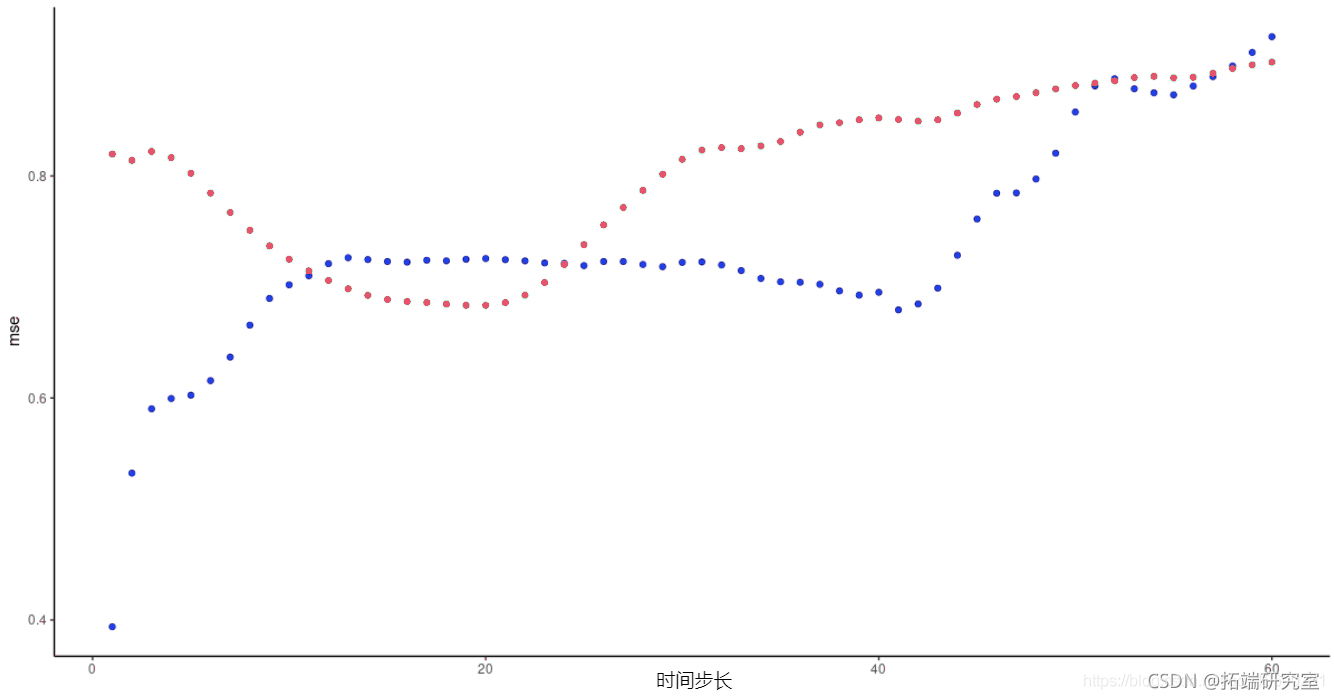
图2:FNN-LSTM和vanilla堆叠LSTM得到的每时间段预测误差,绿色:LSTM,蓝色:FNN-LSTM。
有趣的是,我们看到FNN-LSTM的预测误差在第一次预测和第二次预测之间 “跳跃”,然后在第二次预测和随后的预测之间 “跳跃”,让人想起潜在代码的变量重要性的类似跳跃。在前10个时间步骤之后,vanilla LSTM已经赶上了FNN-LSTM,我们不会仅仅根据一次运行的输出来解释损失的发展。
相反,让我们检查一下实际的预测结果。我们从测试集中随机挑选序列,并要求FNN-LSTM和vanilla LSTM进行预测。其他数据集也将遵循同样的程序。
bind_rows(given, lstm, fnn) ggplot(comp\_preds\_df, aes(num, .data, color = type)) + geom_line() +
这里有16个随机抽取的测试集的预测结果。基本事实显示为粉红色;蓝色预测来自FNN-LSTM,绿色预测来自vanilla LSTM。
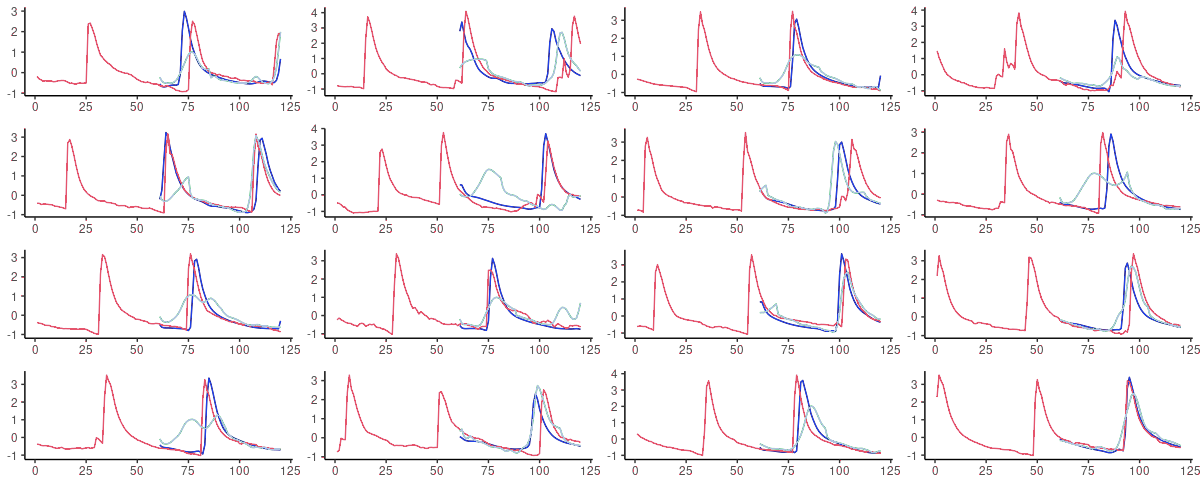
图3:FNN-LSTM(蓝色)和vanilla LSTM(天蓝色)对测试集中随机选择的序列进行的60步提前预测。粉红色:基础事实数据。
我们从误差检查中所期望的结果是真实的。FNN-LSTM对一个给定序列的即时连续性产生了明显更好的预测。
电力数据集
这是一个关于电力消耗的数据集,聚集了321个不同的家庭和15分钟的时间间隔。
数据对应的是2012年至2014年期间321个家庭的平均耗电量,单位为15分钟内消耗的千瓦数。
在这里,我们看到一个非常有规律的模式。
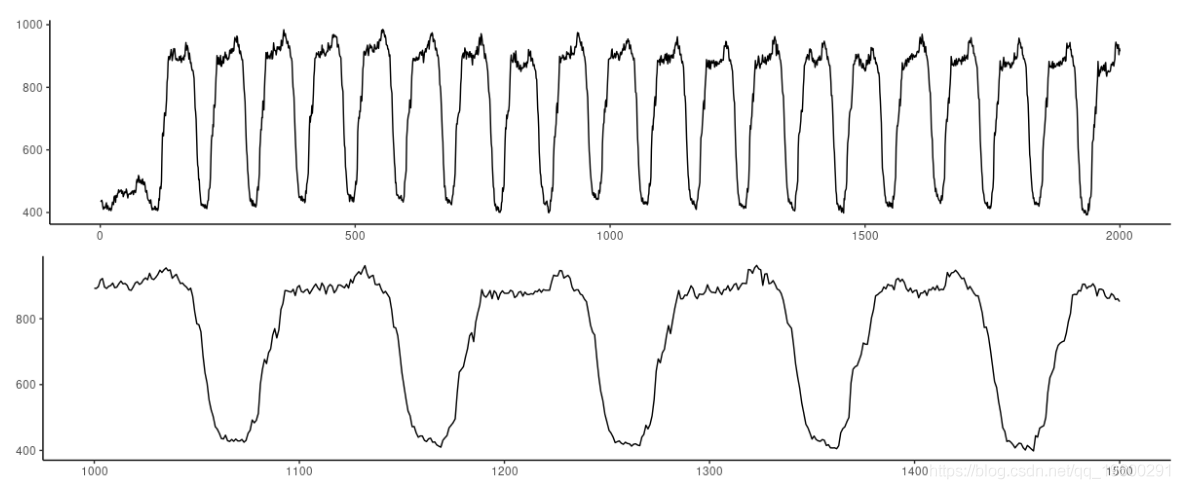
图4:电力数据集。顶部:前2000个观测值。底部。放大500个观测值。
发现这样有规律的模式,我们立即尝试预测更多的时间步数(120)。
对于fnn_multiplier为0.5,潜变量方差看起来是这样的。

我们肯定看到在第一个变量之后已经有了急剧的下降。
两种架构上的预测误差如何比较?
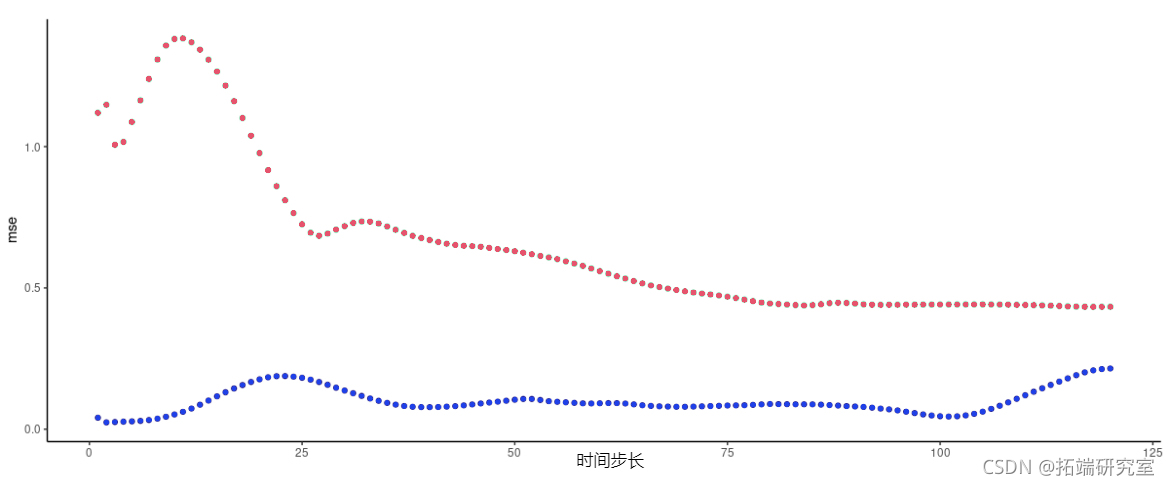
图5:FNN-LSTM和vanilla堆叠LSTM得到的每时间段预测误差。天蓝色:LSTM,蓝色:FNN-LSTM。
在这里,FNN-LSTM在很长的时间段内表现得更好,但同样,这种差异在即时预测中是最明显的。对实际预测的检查能否证实这一观点?
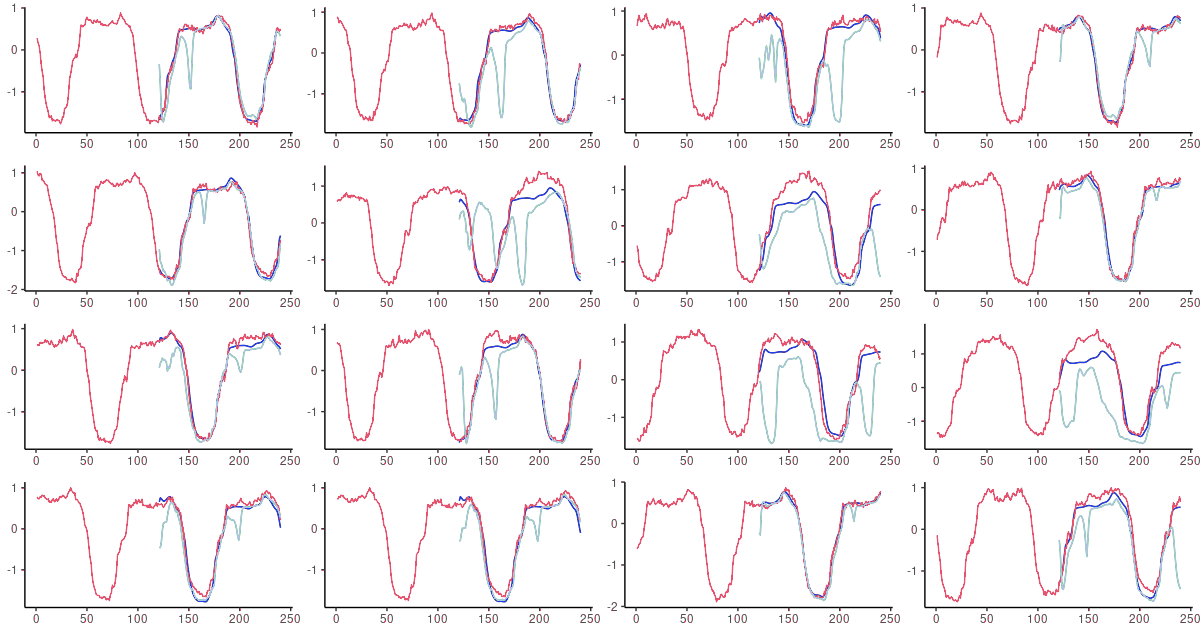
图6:FNN-LSTM(蓝色)和vanilla LSTM(天蓝色)对测试集中随机选择的序列的60步超前预测。粉红色:基础事实。
FNNN-LSTM的预测在所有时间尺度上都表现不错。
现在我们已经看到了简单和可预测的情况,让我们来看看其他情况。
心电图数据集
对应的是两个不同病人的心电图测量结果。
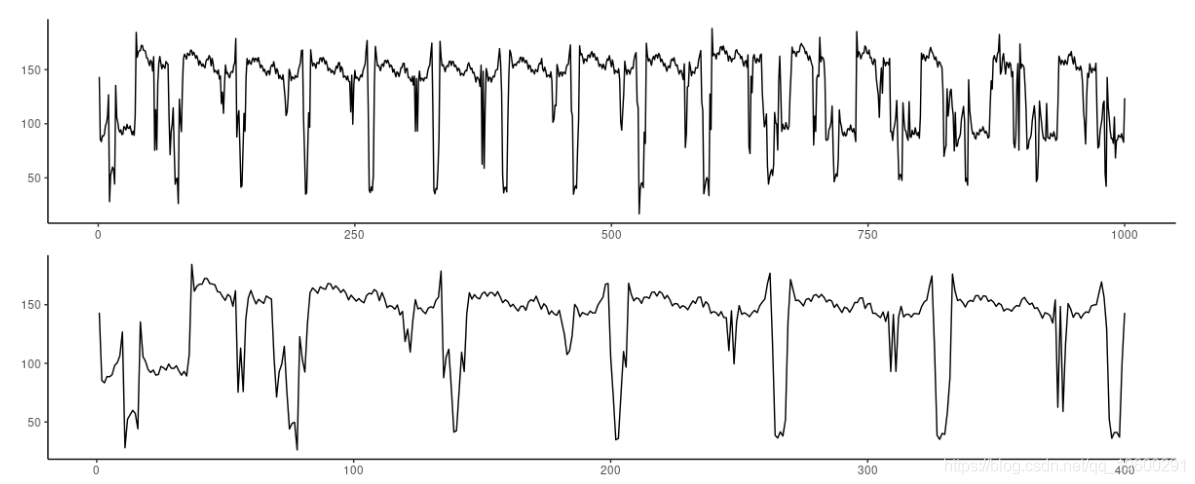
图7:心电图数据集。顶部:前1000个观测值。底部:放大前400个观测值。
看起来并不像预期的那样有规律。第一次实验表明,两个架构都无法处理大量的时间段。在每一次尝试中,FNN-LSTM在最开始的时间步数上表现更好。
n\_timesteps=12的情况也是如此,这是最后一次尝试(120、60和30之后)。在fnn\_multiplier为1的情况下,所获得的潜在方差为:

第一个变量和所有其他变量之间存在差距;但V1也没有解释多少方差。
除了第一次预测,vanilla LSTM这次显示了较低的预测误差;但是,我们必须补充一点,在试验其他时间步长设置时,并没有持续观察到这一点。
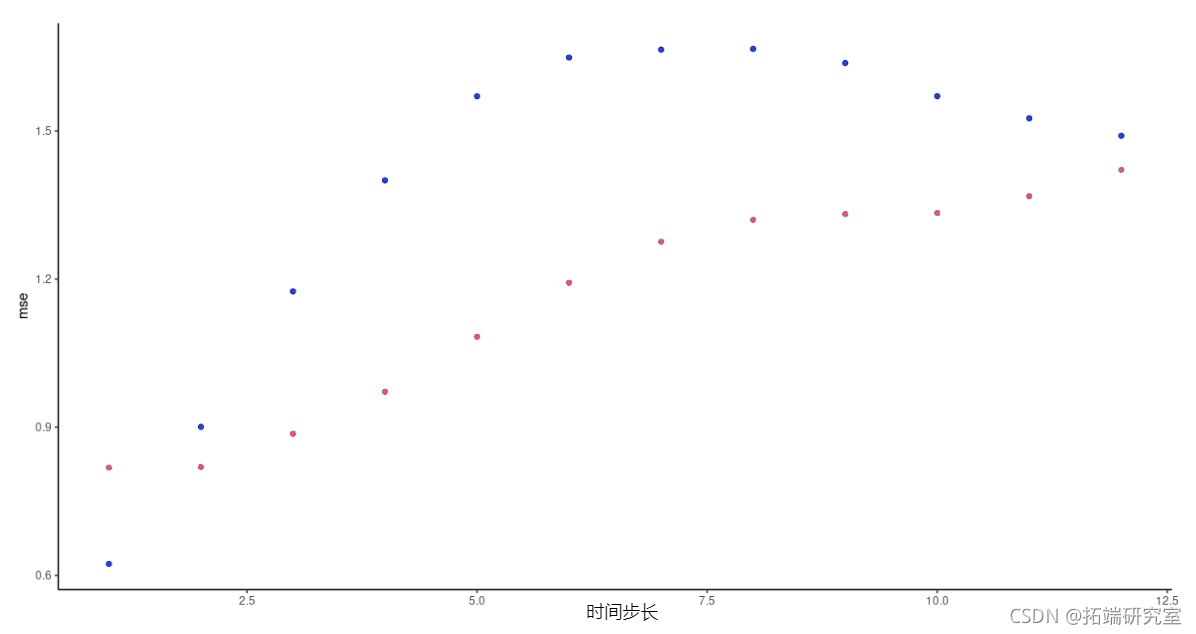
图8:FNN-LSTM和vanilla堆叠LSTM得到的每个时间段的预测误差。绿色:LSTM。蓝色:FNN-LSTM。
从实际预测来看,这两种架构在持久性预测充分的情况下表现最好–事实上,即使在不充分的情况下,它们也会产生一个预测。
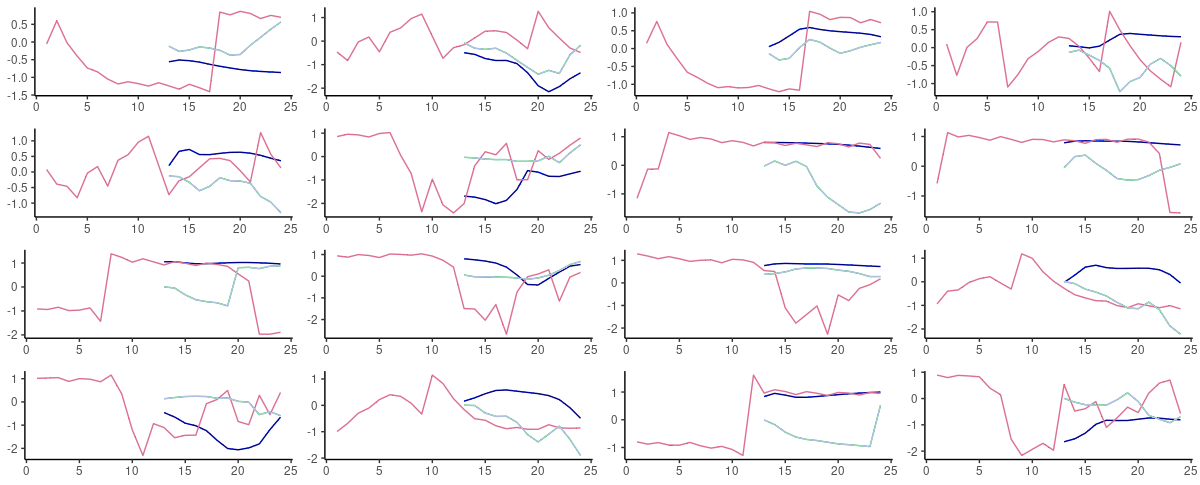
图9:FNN-LSTM(蓝色)和vanilla LSTM(绿色)对测试集中随机选择的序列的60步超前预测。粉红色:基础事实。
在这个数据集上,我们当然希望探索其他能够更好地捕捉数据中的高低频率的架构,比如混合模型。但是–如果我们选择可以做一步到位的滚动预测,我们会选择FNN-LSTM。
小鼠数据集
“小鼠”,这是从小鼠丘脑中记录的尖峰率。
小鼠丘脑中一个神经元的尖峰率时间序列。
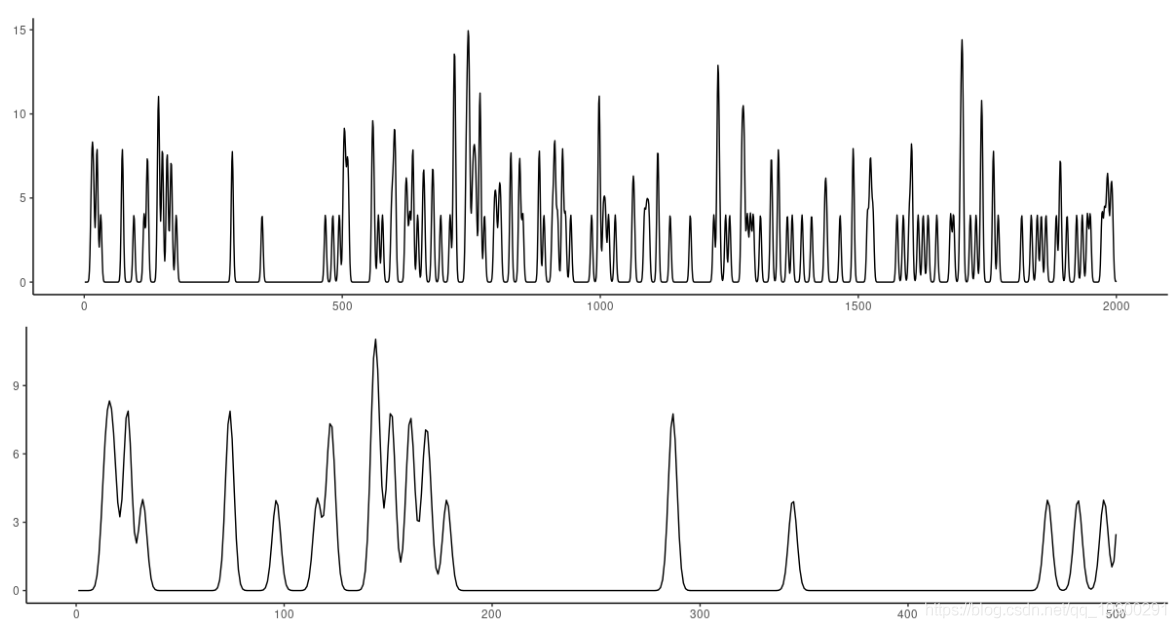
图10:小鼠数据集。顶部:前2000个观察值。底部:放大前500个观测值。
很明显,这个数据集将是很难预测的。
像往常一样,我们检查潜在的代码变异(fnn_multiplier被设置为0.4)。

同样,我们没有看到第一个变量解释了很多方差。不过,有趣的是,当检查预测误差时,我们得到的情况与我们在第一个喷泉数据集上得到的情况非常相似。
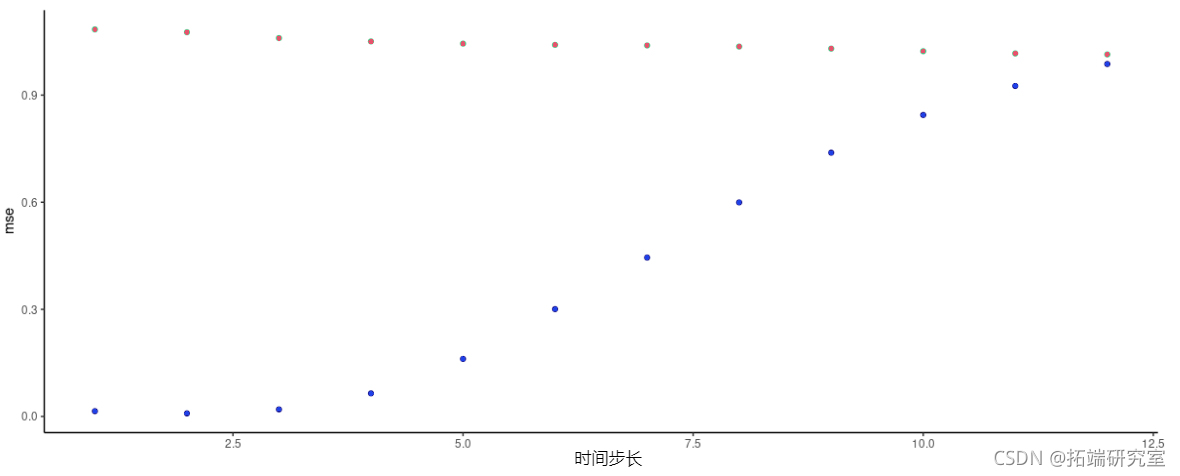
图11:FNN-LSTM和vanilla堆叠LSTM得到的每时间段预测误差。天蓝色:LSTM。蓝色:FNN-LSTM。
因此,在这里,潜在代码似乎绝对是有帮助的, 随着我们试图预测的时间步数 “增加”,预测性能不断下降–或者反过来说,短时预测应该是相当好的!我们可以看到:在一个小时内,我们的预测结果是:
让我们来看看。
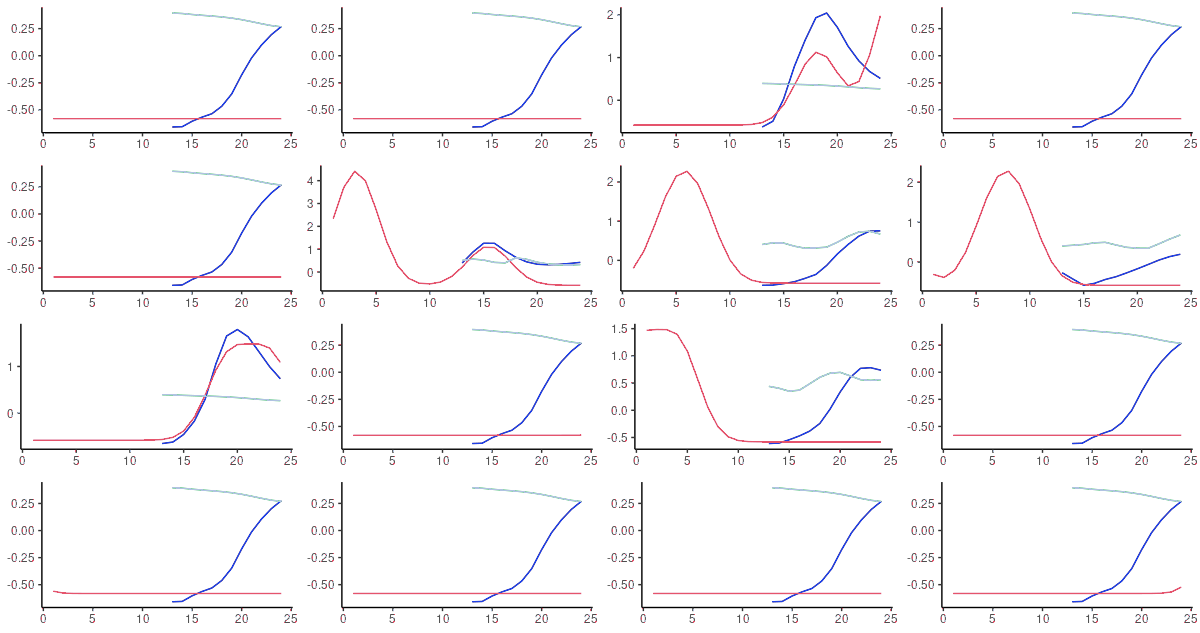
图12:FNN-LSTM(蓝色)和vanilla LSTM(天蓝色)对测试集中随机选择的序列进行的60步超前预测。粉红色:基础事实。
事实上,在这个数据集上,两个架构之间的行为差异是惊人的。vanilla LSTM在数据的平均值附近产生 “平坦 “的曲线,而FNN-LSTM在收敛到平均值之前接近实际值。选择FNN-LSTM–如果我们要从这两者中选择一个–对这个数据集来说是一个明显的决定。
讨论
在整个文本中,我们一直强调实用性–如何使用这种技术来改善预测?但是,看了上述结果,我们想到了一些有趣的问题。我们已经猜测,潜在代码中高变量的数量是否与我们能合理预测未来的程度有关。然而,更耐人寻味的是,数据集本身的特点如何影响FNN的效率。
这些特征可能是:
- 数据集的非线性程度如何?(换句话说,如某种形式的测试算法所示,它与数据生成机制是线性机制的假设有多不兼容?)
- 该系统在多大程度上对初始条件有敏感依赖?
- 它的(估计的)维度是什么,例如,在相关维度方面?
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 时序预测、深度强化学习与蒙特卡洛模拟融合:LSTM、GRU、Attention、DQN及多策略智能体的股票交易决策体系构建——以Google股价为例 | 附代码数据
时序预测、深度强化学习与蒙特卡洛模拟融合:LSTM、GRU、Attention、DQN及多策略智能体的股票交易决策体系构建——以Google股价为例 | 附代码数据 CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据
CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据 Python可口可乐股票交易数据分析:KMeans-RF-LSTM多模型融合聚类、随机森林回归价格预测与交易模式识别
Python可口可乐股票交易数据分析:KMeans-RF-LSTM多模型融合聚类、随机森林回归价格预测与交易模式识别 Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据



