极值理论关注风险损失分布的尾部特征,通常用来分析概率罕见的事件,它可以依靠少量样本数据,在总体分布未知的情况下,得到总体分布中极值的变化情况,具有超越样本数据的估计能力。
因此,基于GPD(generalized pareto distribution)分布的模型可更有效地利用有限的巨灾损失数据信息,从而成为极值理论当前的主流技术。
针对巨灾发生频率低、损失高、数据不足且具有厚尾性等特点,利用GPD模型对火灾经济损失数据进行了统计建模;并对形状参数及尺度参数进行了估计。
可下载资源
视频
R语言极值理论EVT：基于GPD模型的火灾损失分布分析
模型检验表明,GPD模型对巨灾风险厚尾特点具有较好的拟合效果和拟合精度,为巨灾风险估计的建模及巨灾债券的定价提供了理论依据。
对数据进行参数化分布拟合有时会导致模型与数据在高密度区域拟合很好，但在低密度区域拟合很差。对于单峰分布，例如正态分布或者 Student t 分布，这些低密度区域称为分布的“尾部”。模型可能在尾部拟合不佳的原因之一在于，尾部的数据显然较少，不足以作为选择模型的依据，因此通常会基于模型拟合众数附近数据的能力来选择模型。另一个原因可能在于，实际数据的分布通常要比常见的参数化模型更复杂。
但是，在许多应用中，尾部数据拟合是主要问题所在。广义帕累托分布 (GP) 应运而生，它能够基于理论参数对各种分布的尾部进行建模。一种使用到 GP 的分布拟合方法是在观测值密集的区域使用非参数化拟合（例如经验累积分布函数），而在数据尾部使用 GP 拟合。
火灾损失数据
本文使用的数据是在再保险公司收集的，包括1980年至1990年期间的2167起火灾损失。已对通货膨胀进行了调整。总索赔额已分为建筑物损失、利润损失。
base1=read.table( "dataunivar.txt",
header=TRUE)
base2=read.table( "datamultiva.txt",
header=TRUE)考虑第一个数据集（到目前为止，我们处理的是单变量极值），
> D=as.Date(as.character(base1$Date),"%m/%d/%Y")
> plot(D,X,type="h")图表如下：
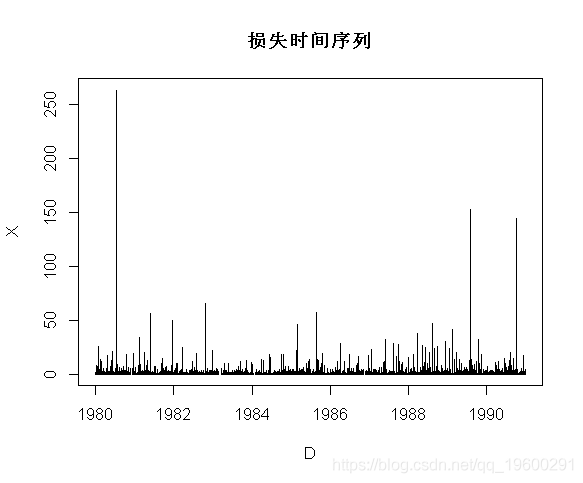
然后一个自然的想法是可视化
例如
> plot(log(Xs),log((n:1)/(n+1)))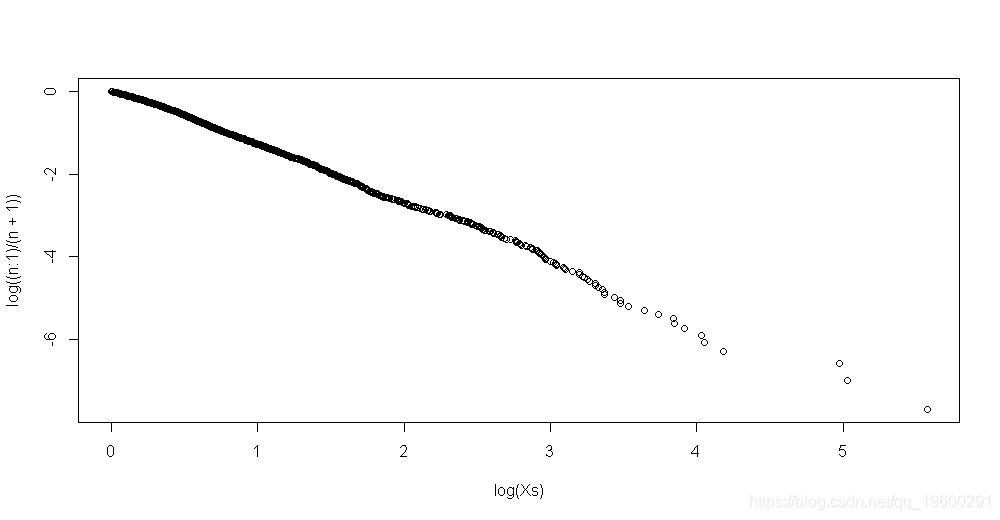
线性回归
这里的点在一条直线上。斜率可以通过线性回归得到，
lm(formula = Y ~ X, data = B)
lm(Y~X,data=B[(n-500):n,])
lm(formula = Y ~ X, data = B[(n - 100):n, ])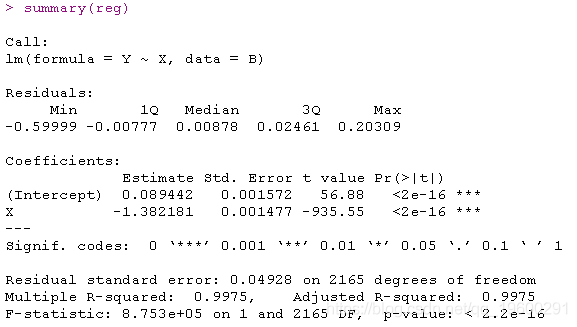 
重尾分布
这里的斜率与分布的尾部指数有关。考虑一些重尾分布
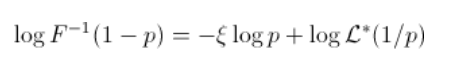
由于自然估计量是阶次统计量，因此直线的斜率与尾部指数相反 . 斜率的估计值为（仅考虑最大的观测值）
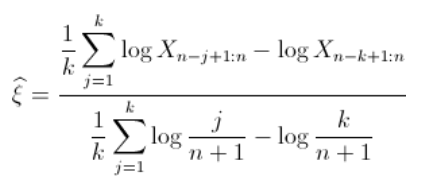
希尔估算量
希尔估算量基于以下假设：上面的分母几乎为1（即等于）。
随时关注您喜欢的主题
那么可以得到收敛性假设。进一步
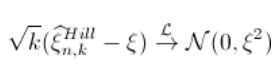
基于这个（渐近）分布，可以得到一个（渐近）置信区间
> xi=1/(1:n)*cumsum(logXs)-logXs
> xise=1.96/sqrt(1:n)*xi
> polygon(c(1:n,n:1),c(xi+xise,rev(xi-xise)),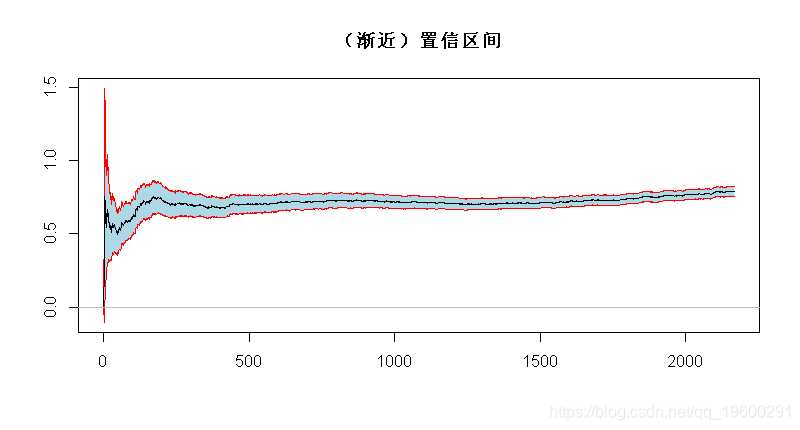 
增量方法
与之类似（同样还有关于收敛速度的附加假设）
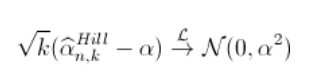
（使用增量方法获得）。同样，我们可以使用该结果得出（渐近）置信区间
> alphase=1.96/sqrt(1:n)/xi
> polygon(c(1:n,n:1),c(alpha+alphase,rev(alpha-alphase)),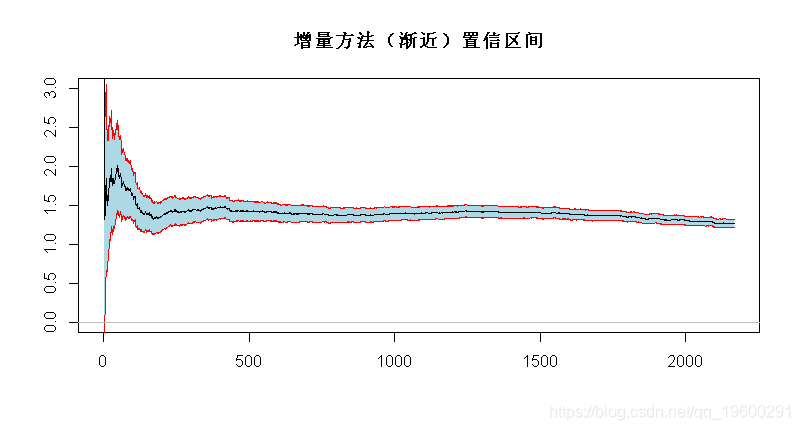 
Deckers-einmal-de-Haan估计量
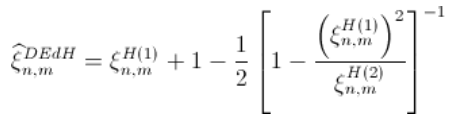
然后（再次考虑收敛速度的条件，即），
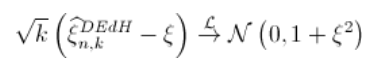
Pickands估计
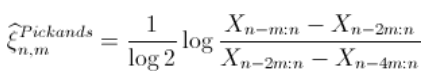
由于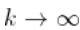 
,
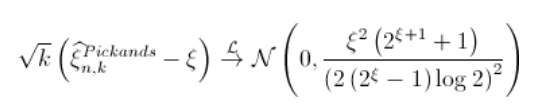
代码
> xi=1/log(2)*log( (Xs[seq(1,length=trunc(n/4),by=1)]-
+ Xs[seq(2,length=trunc(n/4),by=2)])/
> xise=1.96/sqrt(seq(1,length=trunc(n/4),by=1))*
+sqrt( xi^2*(2^(xi+1)+1)/((2*(2^xi-1)*log(2))^2))
> polygon(c(seq(1,length=trunc(n/4),by=1),rev(seq(1,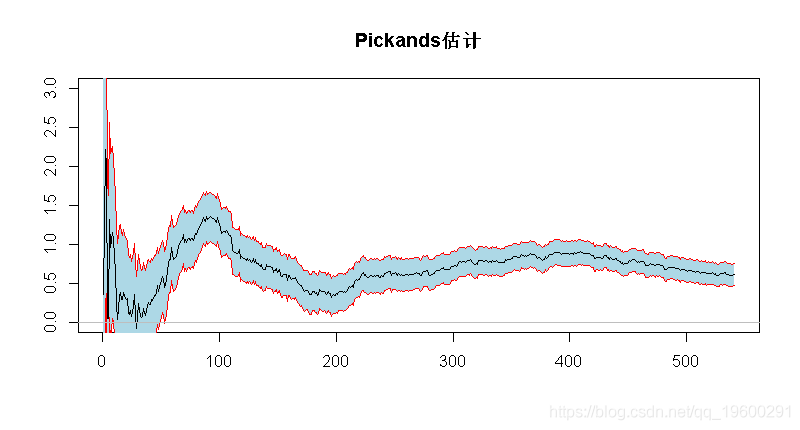 
拟合GPD分布
也可以使用最大似然方法来拟合高阈值上的GPD分布。
> gpd
$n
[1] 2167
$threshold
[1] 5
$p.less.thresh
[1] 0.8827873
$n.exceed
[1] 254
$method
[1] "ml"
$par.ests
xi beta
0.6320499 3.8074817
$par.ses
xi beta
0.1117143 0.4637270
$varcov
[,1] [,2]
[1,] 0.01248007 -0.03203283
[2,] -0.03203283 0.21504269
$information
[1] "observed"
$converged
[1] 0
$nllh.final
[1] 754.1115
attr(,"class")
[1] "gpd"或等效地
> gpd.fit
$threshold
[1] 5
$nexc
[1] 254
$conv
[1] 0
$nllh
[1] 754.1115
$mle
[1] 3.8078632 0.6315749
$rate
[1] 0.1172127
$se
[1] 0.4636270 0.1116136它可以可视化尾部指数的轮廓似然性，
> gpd.prof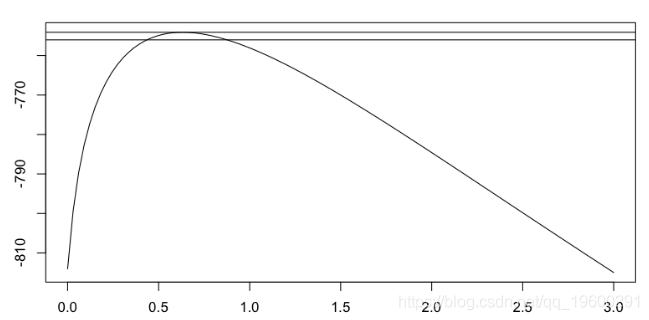
或者
> gpd.prof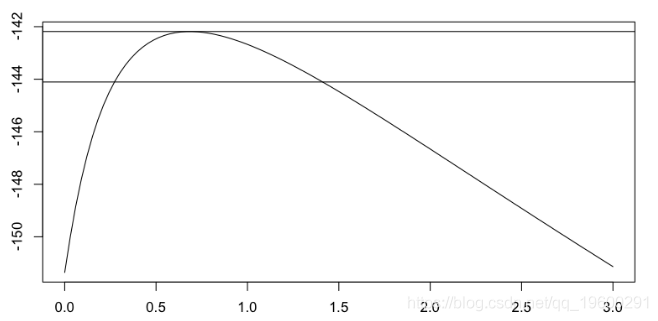
因此，可以绘制尾指数的最大似然估计量，作为阈值的函数（包括置信区间），
Vectorize(function(u){gpd(X,u)$par.ests[1]})
plot(u,XI,ylim=c(0,2))
segments(u,XI-1.96*XIS,u,XI+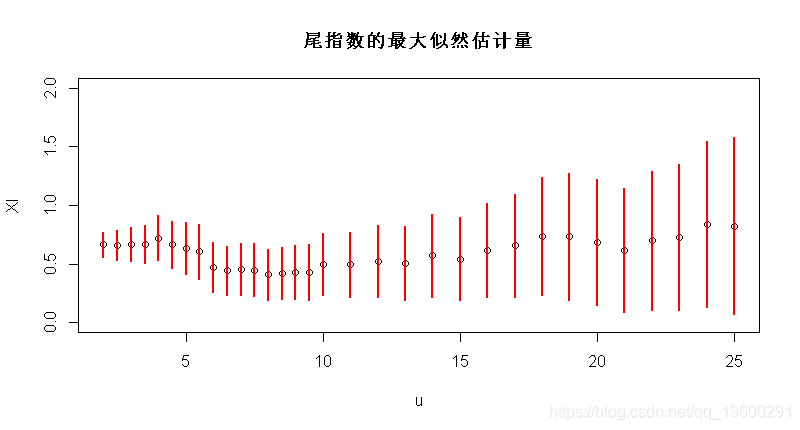 
最后，可以使用块极大值技术。
gev.fit
$conv
[1] 0
$nllh
[1] 3392.418
$mle
[1] 1.4833484 0.5930190 0.9168128
$se
[1] 0.01507776 0.01866719 0.03035380尾部指数的估计值是在这里最后一个系数。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
R语言极值分析：GEV与GPD模型与MCMC的海洋观测数据极值模拟可视化研究
Python用GARCH对ADBL股票价格时间序列趋势滚动预测、损失、可视化分析
