在回归模型研究中，我们将讨论优化，而经典工具就是所谓的共轭。给定函数f：Rp→R，其共轭值为函数f ⋆：Rp→R使得
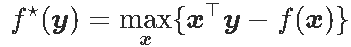
可视化考虑一个简单的抛物线函数（在维度1中）f（x）= x ^ 2 / 2，然后f ⋆（2）是线x↦2x与函数f（x）之间的最大距离。
f = function(x) x^2/2
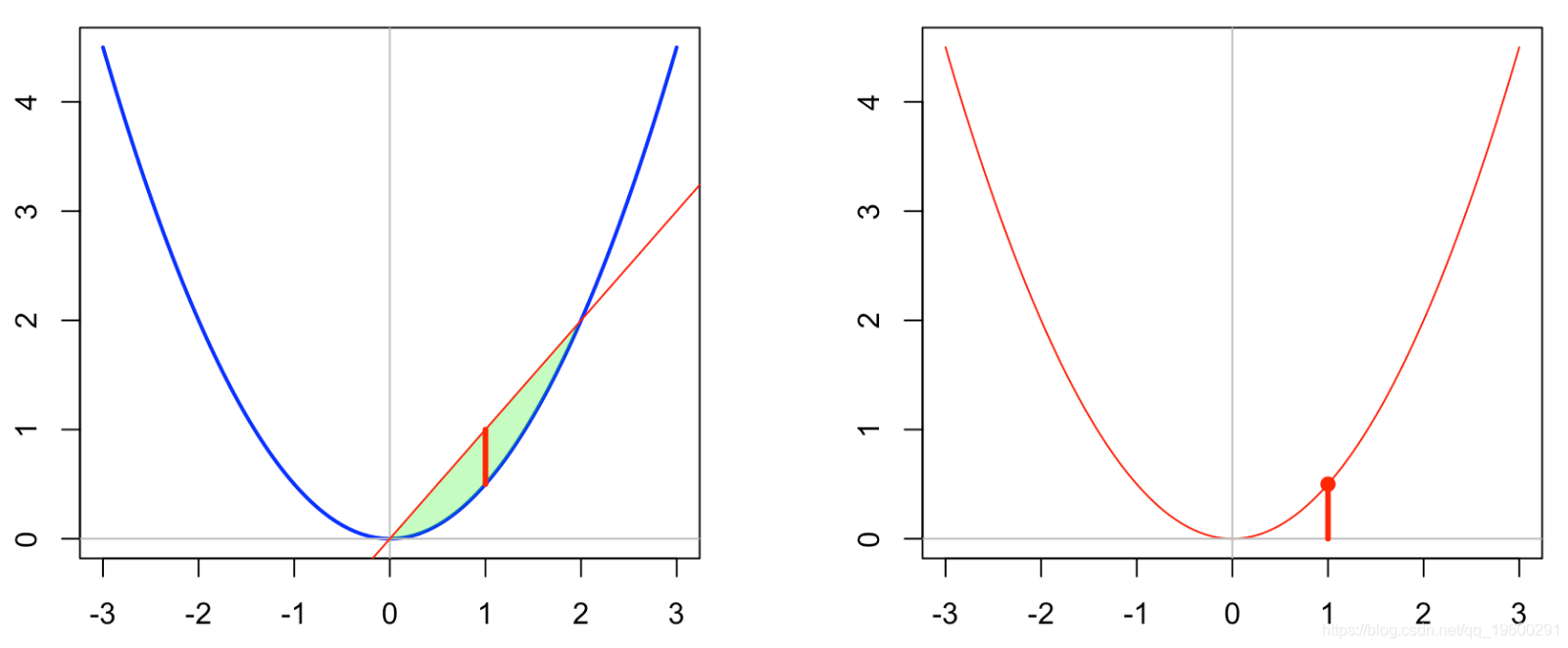
fstar = function(y) max(y*x-vf)我们可以在下图上看到。
polygon(c(x[idx2],rev(x[idx2])),c(vf[idx2],rev(x0*x[idx2],col=rgb(0,1,0,.3,border=NA)
abline(a=0,b=x0,col="red")
segments(x[i],x0*x[i],x[i],f(x[i]),lwd=3,col="red")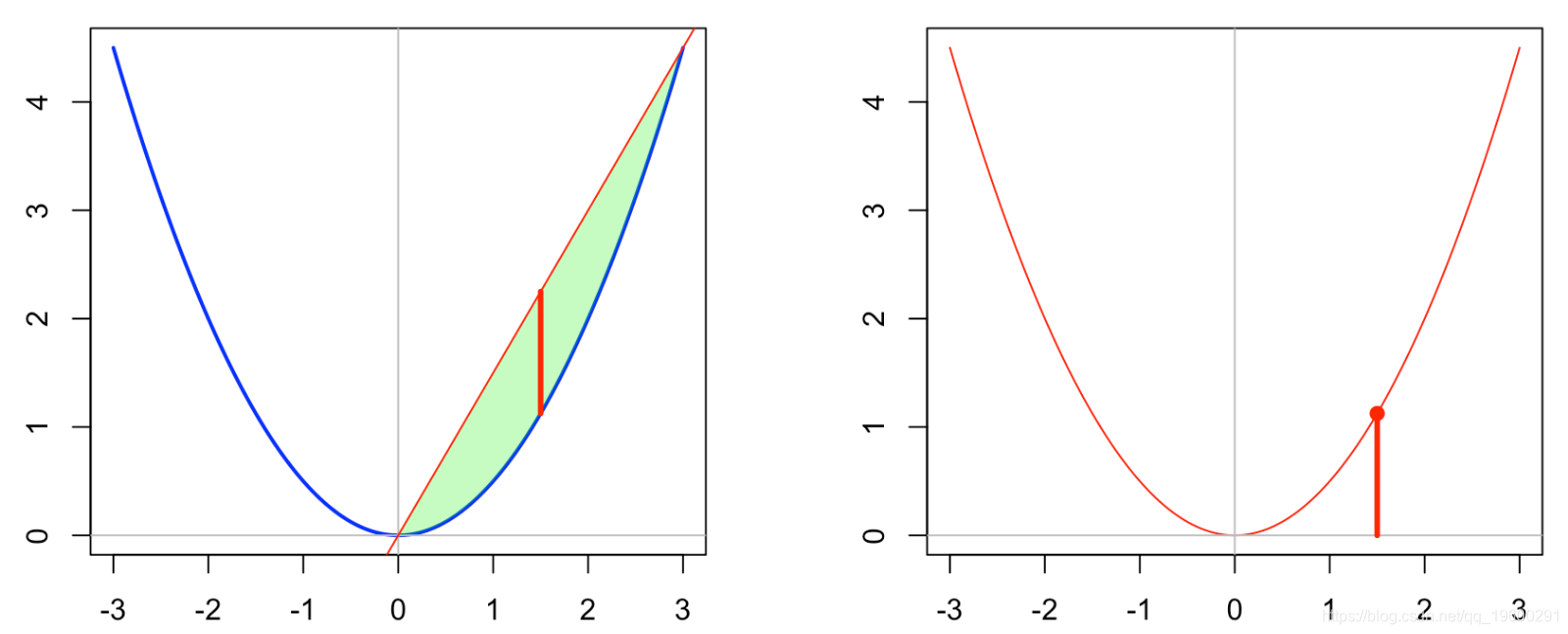
在这种情况下，我们实际上可以计算f⋆，因为
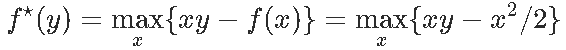
一阶条件是x⋆= y，因此
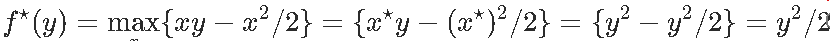
实际上，对于ℓp的共轭，我们可以使用以下代码对其进行可视化
f = function(x) abs(x)^p/p
fstar = function(y) max(y*x-vf)
vi(1.5)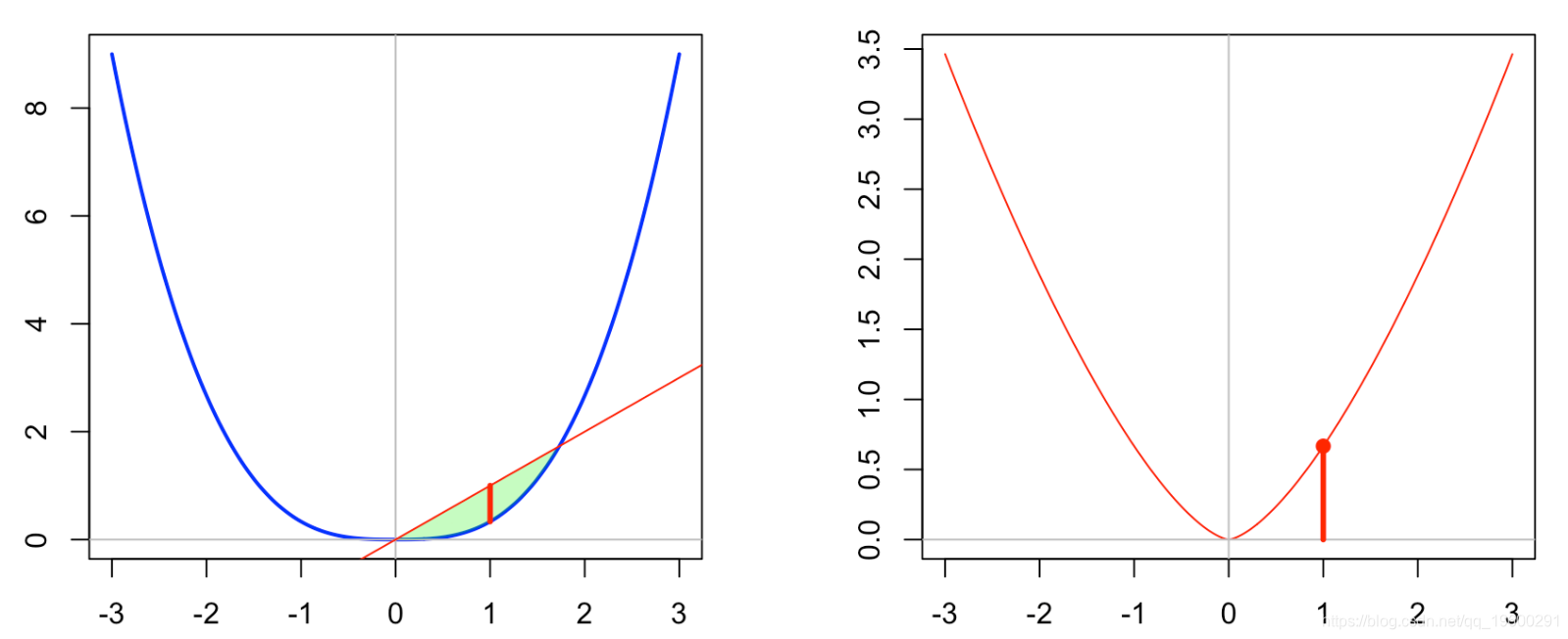
f = function(x) abs(x)^p/p
fstar = function(y) max(y*x-vf)
vi(1, YL=c(0,10))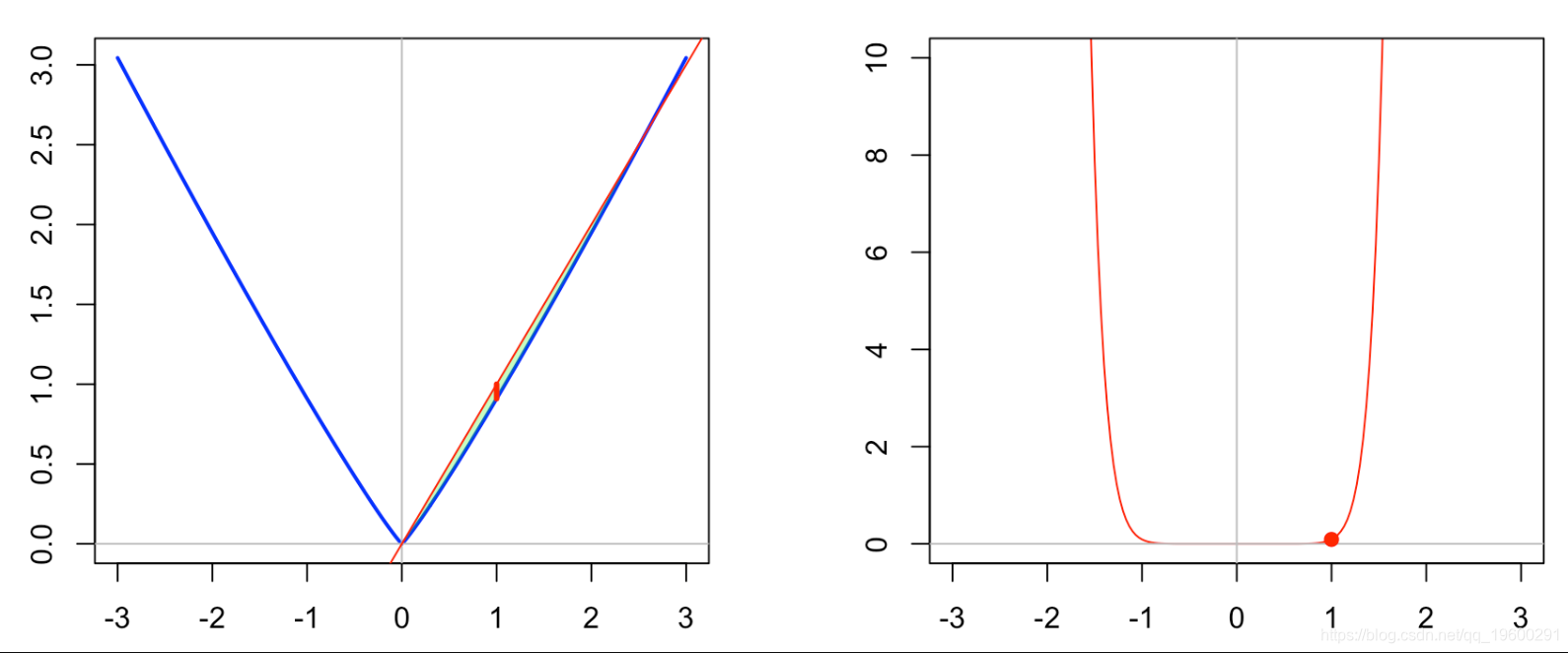
在那种情况下，如果f（x）= ∣x∣则
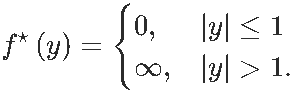
另一种情况是
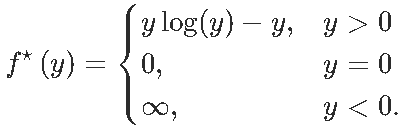
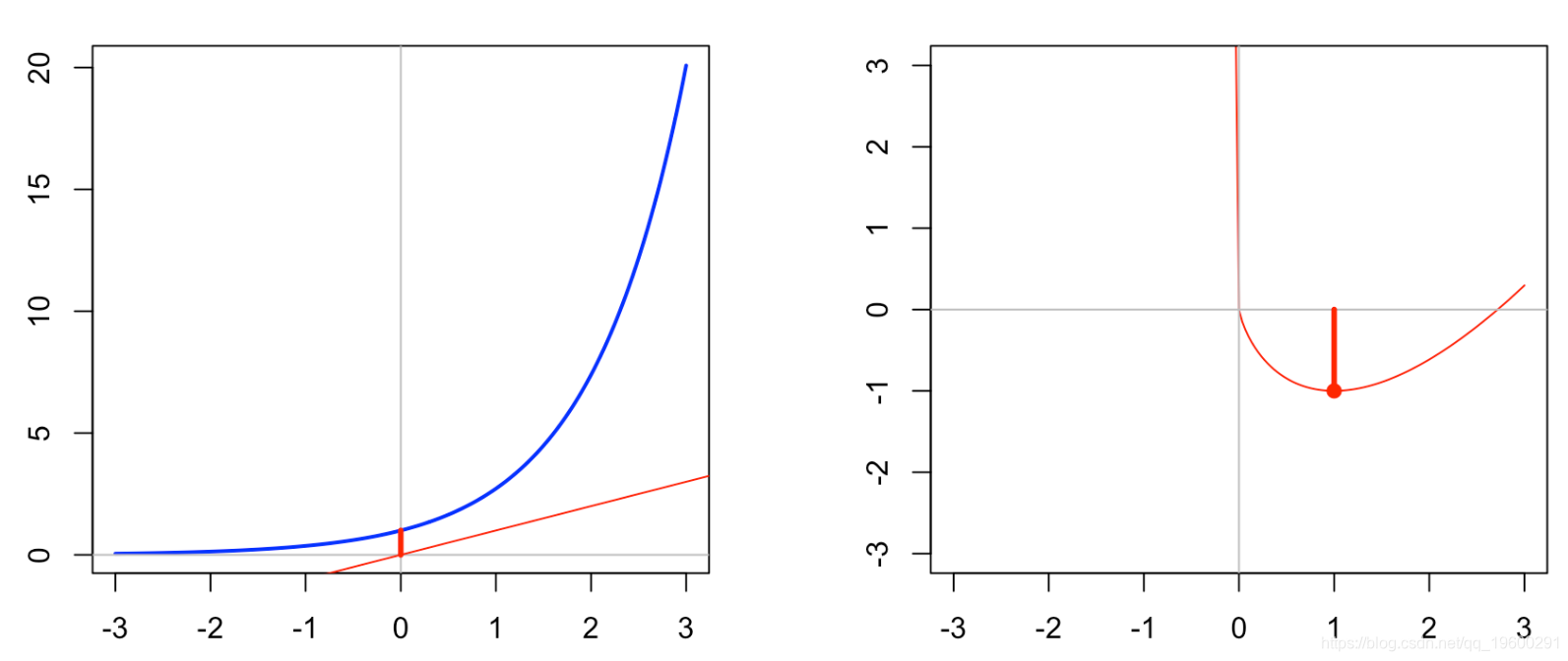
我们可以在下面看到
f = function(x) exp(x)
fstar = function(y) max(y*x-vf)
vi(1,YL=c(-3,3))
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python农业气象预测：优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
