最近我们被客户要求撰写关于聚类技术的研究报告。为了说明层次聚类技术和k-均值，我使用了了城市温度数据集，其中包括几个城市的月平均气温。
我们有15个城市，每月进行一次观测
可下载资源
boxplot(temp[,1:12],main="月平均温度")
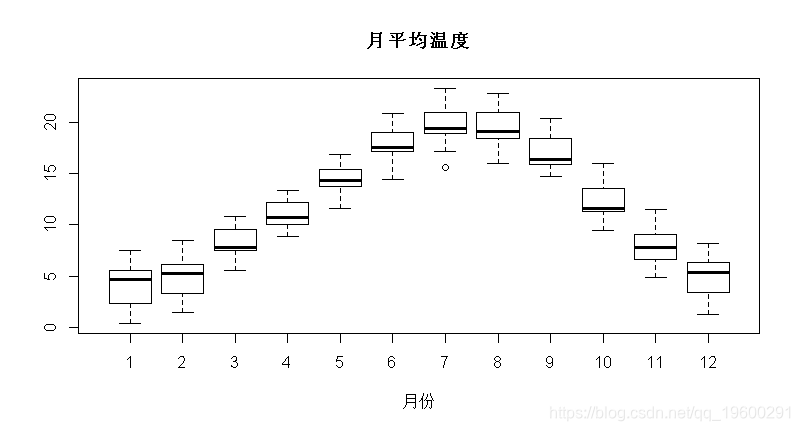
由于方差看起来相当稳定，我们不会将这里的变量“标准化”，
> apply(月份,2,sd)
视频
主成分分析PCA降维方法和R语言分析葡萄酒可视化实例
视频
KMEANS均值聚类和层次聚类：R语言分析生活幸福质量系数可视化实例
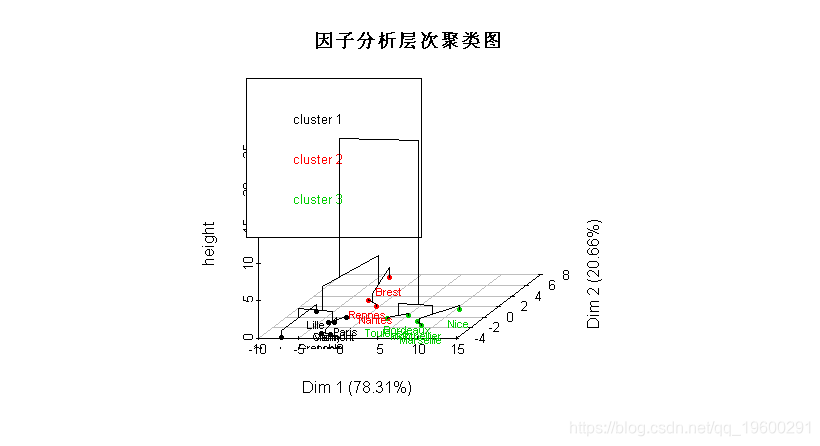
为了得到一个层次聚类分析，使用实例
hclust(dist , method = "ward")
另一种选择是使用
> plot(h2)
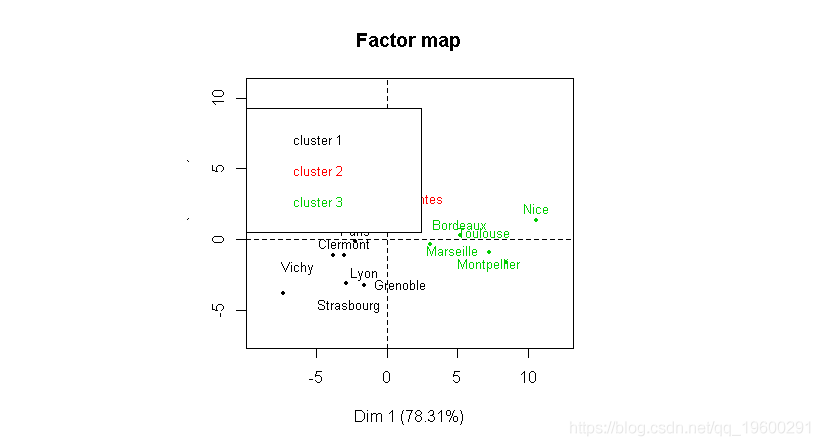
在这里，我们用主成分分析将观察结果可视化。我们这里还有一个自动选择类的数目，这里是3个。我们可以得到组的描述
或直接
cutree(cah,3)
我们也可以自己可视化这些类，
PCA(X,scale.unit=FALSE)
plot( ind$coord[,1:2],col="white")
text( ind$coord[,1],acp$ind$coord[,2],
可以绘制出这些簇的中心点
随时关注您喜欢的主题
> points(PT$Dim.1,PT$Dim.2,pch=19)如果我们在这些中心周围添加Voronoi集，我们看到的是中间的点，恰好是三个区域的交点
vormo(PT$Dim.1,PT$Dim.2)
plot(V,add=TRUE)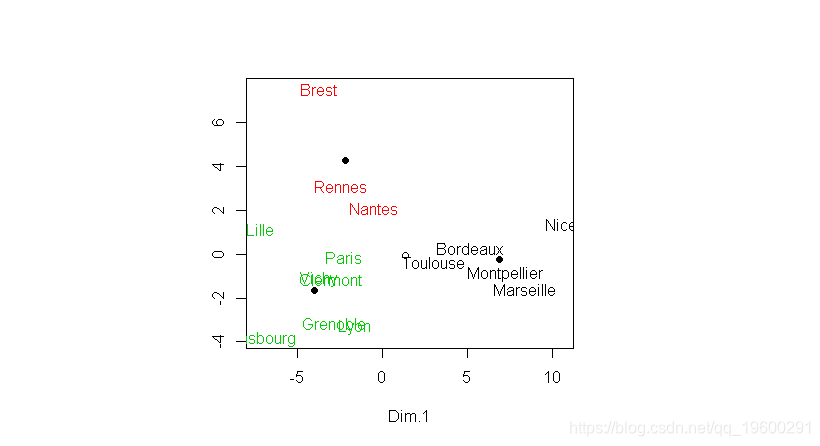
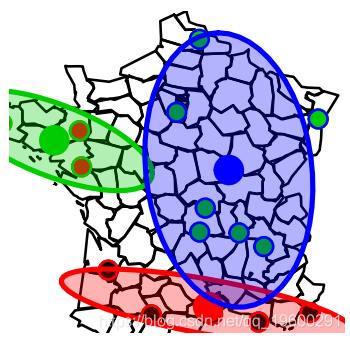
要可视化这些区域，请使用Voronoi图，它又叫泰森多边形或Dirichlet图。
Voronoi图是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。
p=function(x,y){
+ which.min((PT$Dim.1-x)^2+(PT$Dim.2-y)^2)
image(vx,vy,z,col=c(rgb(1,0,0,.2),
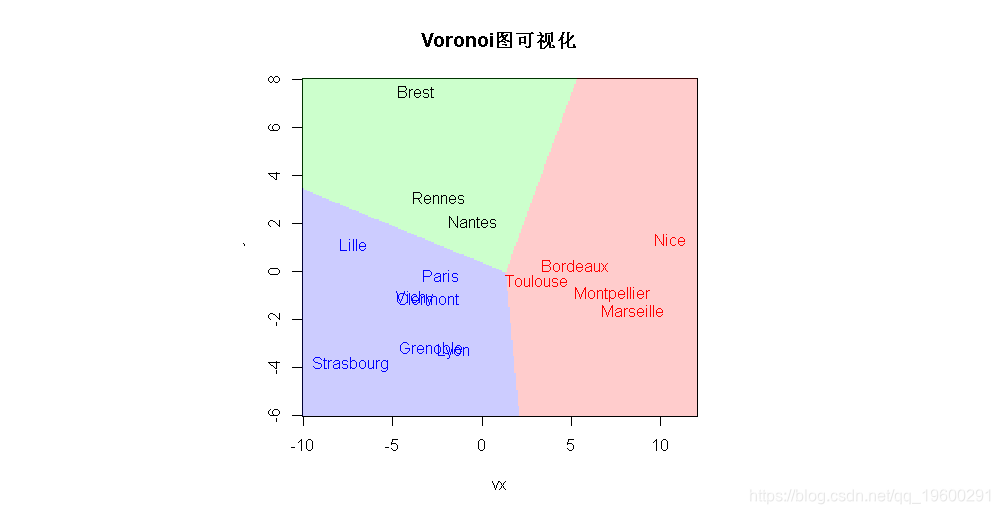
实际上，这三组（和这三个区域）也是我们用k-均值算法得到的，
kmeans(coord[,1:2],3)
K-means clustering
with 3 clusters of sizes 3, 7, 5由于我们有一些空间数据，我们可以在地图上把它们可视化
points(Long,Lati,col=groups.3)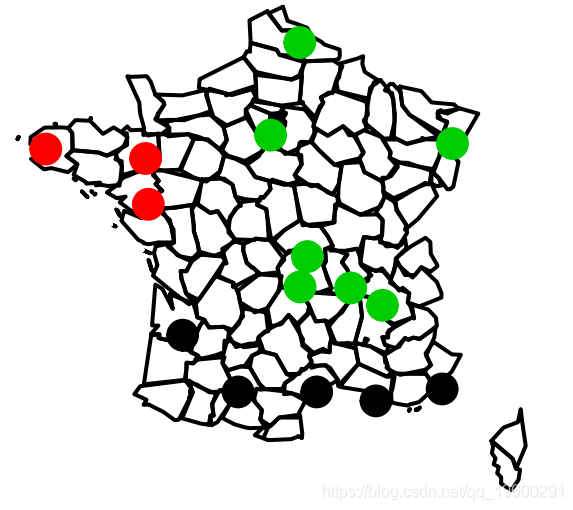
或者，为了可视化这些区域，使用
for(i in 1:3)
+ Ellipse( Long[groups.3==i],
Matlab古代玻璃制品化学成分数据鉴别：K近邻回归、聚类、决策树、随机森林、卡方检验、相关性分析
Python丁香医生平台医生与患者评论数据分析：LightGBM、LDA主题模型、因果推断、聚类、PSM| 附代码数据
视频：Python对多行业板块股票数据LSTM深度学习多任务学习预测：SMA、RSI及K-means聚类实现涨跌趋势与价格联合预测
Python酒店预订数据：随机森林与逻辑回归模型ROC曲线可视化
