
如何使用蒙特卡洛模拟来推导随机变量可能的分布,我们回到统计数据(无协变量)进行说明。
我们假设观察值是基础随机变量,具有未知分布的随机变量。
这里有两种策略。在经典统计中,我们使用概率定理来推导随机变量的属性在可能的情况下的分布。另一种方法是进行计算统计。
对于评估拟合度,测试正态性不是很有用。在本文中,我想说明这一点。我们使用男生的身高数据,
最优化问题的计算方法是很重要的,因为很多最优化的问题难于解析地解出来,对于动态模拟,通常人们能够解析地确定定常态的行为,但是关于瞬态行为的研究则需要计算机模拟,概率模型更加复杂,不具有时间动态特性的模拟有时能够解析地求解出来,且对于简单的随机模型,定常态的结果通常是可用的,但是对于许多情况,概率模型是用模拟的方法解出的。下面我们将讨论概率模型中一些最常用的模拟方法。
随机过程中包含有瞬时或时变的行为的问题通常是很难解析地解出的。蒙特卡罗模拟是有效地解决这一类问题的一般建模技术。模型直观且易于解释,同时也是对许多复杂的随机系统进行建模的仅有的办法。它是基于诸如抛硬币这类简单的随机化处理的办法,但通常使用了计算机的伪随机发生器。由于包含随机元素,所以每次重复会得到不同的结果。
例:假期即将到来,气象局预报假期中每天的降雨概率是50%,请问连续3天都下雨的概率是多少?
使用五步分析法。
第一步提出问题。在这个过程中我们选定一些重要的变量,同时明确我们关于这些变量的假设。第一步的结果列于下图。

第二步选择建模方法,我们使用蒙特卡罗模拟的方法。蒙特卡罗模拟是可以用于任何概率模型的技术。一个概率模型包含有若干个随机变量,必须明确每一个随机变量的概率分布。蒙特卡罗模拟使用随机化的设备按照™的概率分布给出每个随机变量的值。因为模拟的结果依赖于随机元素,所以接连重复同样的模拟会产生不同的结果,通常蒙特卡罗模拟会被重复若干次,以便于确定平均数或期望的结果。第三步,推导模型的数学表达式。

第四步求解问题,我们在计算机上运行上述程序,令参数p=0.5,n=100.看输出结果。结果显示100周中有63周下雨超过连续的3天。第五步,你的长达一周的假期到了,你发现气象台预报每天的降雨概率为0.5,则假期中降雨超过连续3天的概率为60%左右。因此,你要做好不能出去浪的心理准备!最后进行灵敏性分析。对降雨概率p进行分析。对p=0.3,0.4,0.5,0.6,0.7的每一种情况分别进行模拟。结果汇总在下表。
| p |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
| S |
16 |
36 |
62 |
78 |
79 |

可见降雨的周数是随p的增加而单调递增的。提高第t天的降雨概率就意味提高了连续3天降雨的概率。我们的模型关于p是相当稳健和灵敏的。
X=Davis$height[Davis$sex=="M"]我们可以可视化其分布(密度和累积分布)
u=seq(155,205,by=.5)
par(mfrow=c(1,2))
hist(X,col=rgb(0,0,1,.3))
lines(density(X),col="blue",lwd=2)
lines(u,dnorm(u,178,6.5),col="black")
Xs=sort(X)
n=length(X)
p=(1:n)/(n+1)
plot(Xs,p,type="s",col="blue")
lines(u,pnorm(u,178,6.5),col="black")
它看起来像正态分布,因此我们可以在左侧添加密度高斯分布,在右侧添加cdf。我不想测试它是否是高斯分布。为了查看此分布是否相关,可以使用蒙特卡洛模拟法
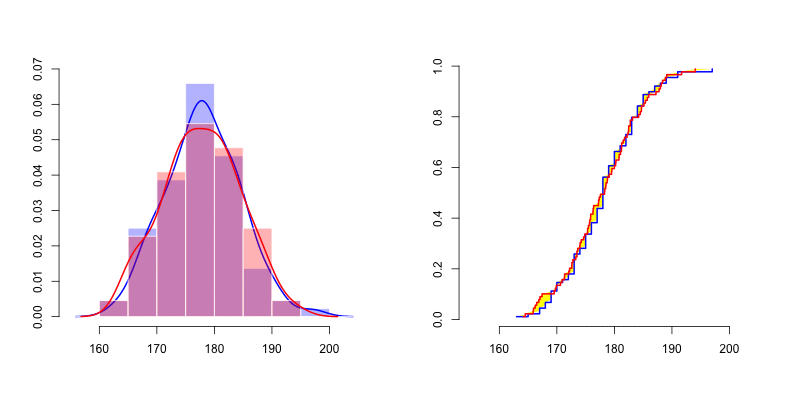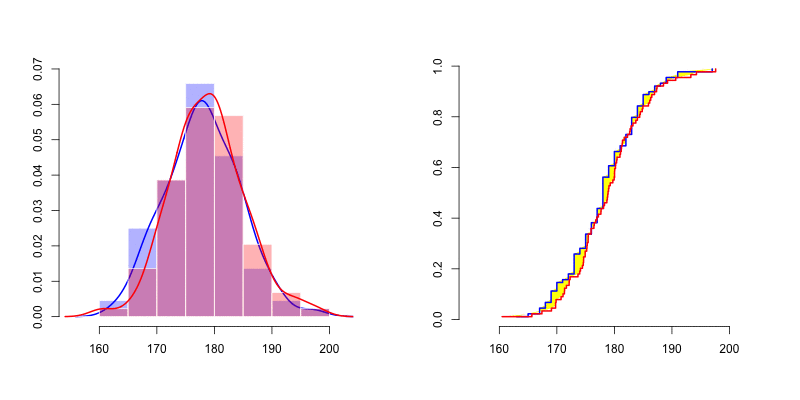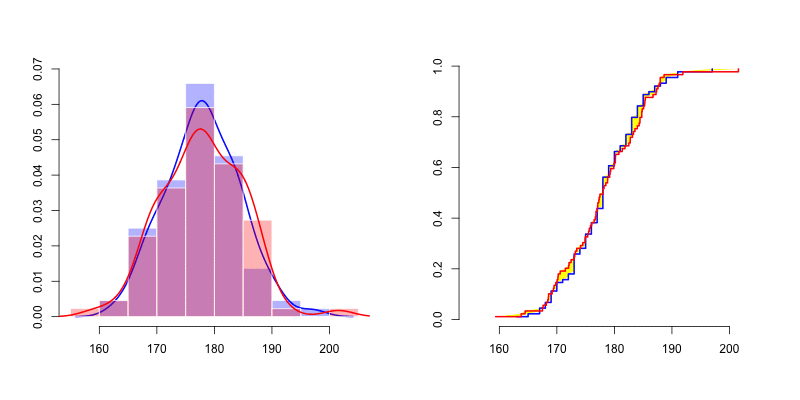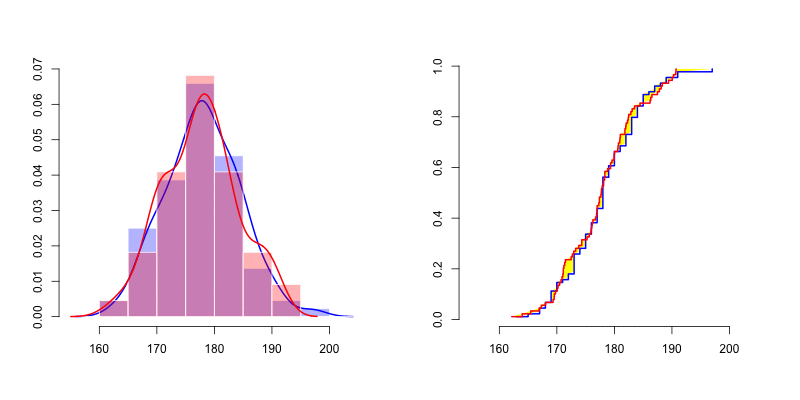
我们可以在左侧看到很难通过密度(直方图以及核密度密度估计器)评估正态性 。人们很难想到两个密度之间的有效距离。但是,如果我们看一下右边的图,我们可以比较经验分布累积分布。如上所述,我们可以按照Cramer-von Mises 检验或 Kolmogorov-Smirnov 距离的建议计算黄色区域 。
如果我们抽取10,000个反事实样本,则可以使用测试统计量等的方法来可视化距离的分布(此处为密度),并将其与样本的观察值进行比较。测试统计量超过观察值的样本比例
mean(dks)
[1] 0.78248计算版本的值
ks.test(X,"pnorm",178,6.5)
One-sample Kolmogorov-Smirnov test
data: X
D = 0.068182, p-value = 0.8079
alternative hypothesis: two-sided在统计数据中,要么操作抽象对象(如随机变量),要么实际上使用一些代码生成假样本以量化不确定性。后者很有趣,因为它有助于可视化复杂的量化。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化
Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析
Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析


