
这里的想法是使距离最大化:想法是区分,所以我们希望样本尽可能不独立。要计算基尼系数。
本文为了说明回归树的构造(使用CART方法),考虑以下模拟数据集,
可下载资源
> set.seed(1)
> n=200
> X1=runif(n)
> X2=runif(n)
> P=.8*(X1<.3)*(X2<.5)+
+ .2*(X1<.3)*(X2>.5)+
+ .8*(X1>.3)*(X1<.85)*(X2<.3)+
+ .2*(X1>.3)*(X1<.85)*(X2>.3)+
+ .8*(X1>.85)*(X2<.7)+
+ .2*(X1>.85)*(X2>.7)
> Y=rbinom(n,size=1,P)
> B=data.frame(Y,X1,X2)具有一个因变量(感兴趣的变量)和两个连续的自变量( 变量
> tail(B)
Y X1 X2
195 0 0.2832325 0.1548510
196 0 0.5905732 0.3483021
197 0 0.1103606 0.6598210
198 0 0.8405070 0.3117724
199 0 0.3179637 0.3515734
200 1 0.7828513 0.1478457理论分区如下
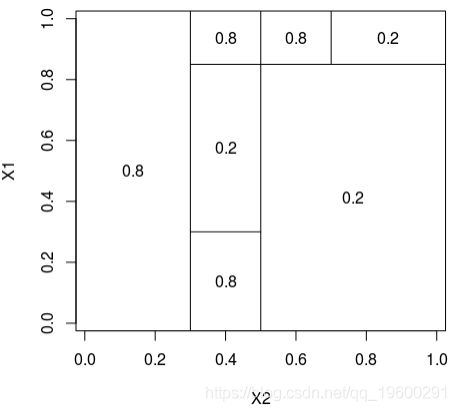
在这里,可以将样本绘制在下方(请注意,第一个变量在上方的y轴上,在下方的x轴上),蓝色点 等于1,红色点等于0,
> plot(X1,X2,col="white")
> points(X1[Y=="1"],X2[Y=="1"],col="blue",pch=19)
> points(X1[Y=="0"],X2[Y=="0"],col="red",pch=19)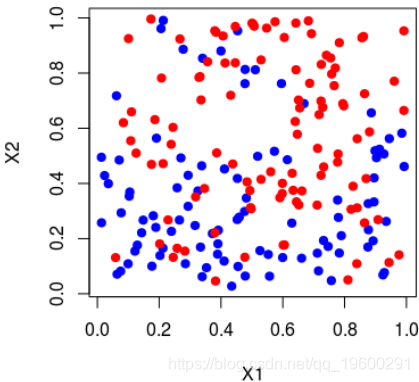
为了构造树,我们需要一个分区critera。最标准的可能是Gini的索引,当将s分为两类时,可以写出该索引, 在此表示
或 将分为三类时,表示为
等等,这里
在传统上,当我们考虑两个等级时,或者在三个等级的情况下。
同样,这里的想法是使距离最大化:想法是区分,所以我们希望样本尽可能不独立。要计算基尼系数,请考虑
> GINI=function(y,i){
+ T=table(y,i)
+ nx=apply(T,2,sum)
+
+
+
+
+
+ }我们只需构造列联表,然后计算上面给出的数量。首先,假设只有一个解释变量。我们将样本一分为二,并使用所有可能的分割值
然后,我们为所有这些值计算基尼系数。结是使基尼系数最大化的值。有了第一个节点后,我们将继续保留(从现在开始将其称为)。
我们通过寻找最佳第二选择来重申:给定一个根节点,考虑将样本一分为三的值,并给出最高的基尼系数,因此,我们考虑以下分区
或这个
也就是说,我们在上一个结的下方或上方分割。然后我们进行迭代。代码可以是这样的,
> for(s in 1:4){
+ for(i in 1:length(u)){
+ vgini[i]=GINI(Y,I)
+ }
+
+
+ cat("knot",k,u[k],"\n")
+
+
+ }
knot 69 0.3025479
knot 133 0.5846202
knot 72 0.3148172
knot 111 0.4811517第一步,基尼系数的值如下:
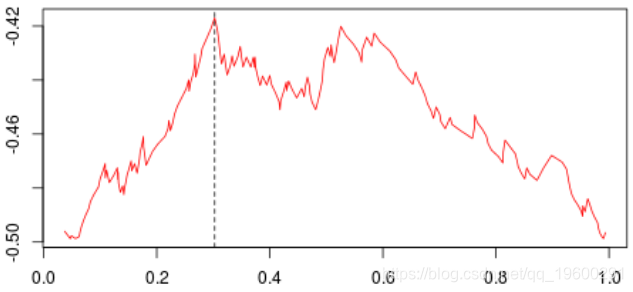
最高约为0.3。然后,我们尝试分三部分构造一个分区(拆分为0.3以下或以上)。我们得到以下基尼系数图(作为第二个节点的函数)
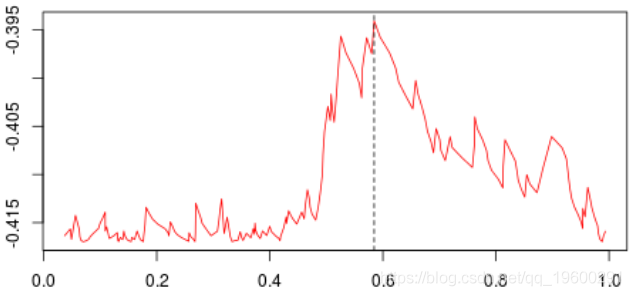
当样本在0.6左右分裂(这成为我们的第二个节点)时最大。等,现在,让我们将代码与标准R函数进行比较,
node), split, n, deviance, yval
* denotes terminal node
1) root 200 49.8800 0.4750
2) X2 < 0.302548 69 12.8100 0.7536 *
3) X2 > 0.302548 131 28.8900 0.3282
6) X2 < 0.58462 65 16.1500 0.4615
12) X2 < 0.324591 7 0.8571 0.1429 *
13) X2 > 0.324591 58 14.5000 0.5000 *
7) X2 > 0.58462 66 10.4400 0.1970 *我们确实获得了类似的结:第一个为0.302,第二个为0.584。因此,构造树并不难…
现在,如果我们考虑两个解释变量,该怎么办?保持不变,除了分区的编写现在变得更加复杂。为了找到第一个节点,我们考虑了两个分量的所有值,然后再次保持最大化基尼指数的值,
> plot(u1,gini[,1],ylim=range(gini),col="green",type="b",xlab="X1",ylab="Gini index")
> abline(h=mg,lty=2,col="red")
> if(i==1){points(u1[which.max(gini[,1])],mg,pch=19,col="red")
+ segments(u1[which.max(gini[,1])],mg,u1[which.max(gini[,1])],-100000)}
> u2[which.max(gini[,2])]
[1] 0.3025479这些图如下所示并获得了右侧的分区,
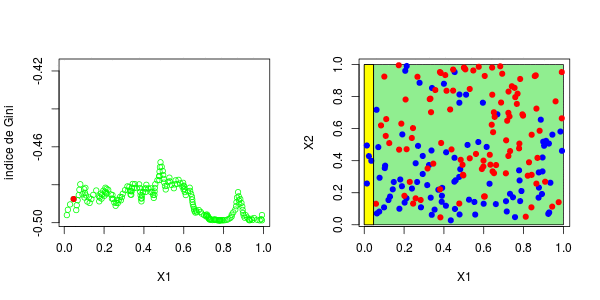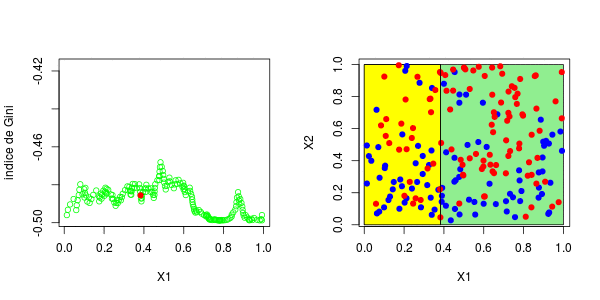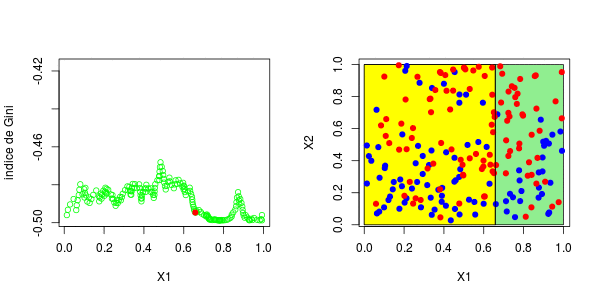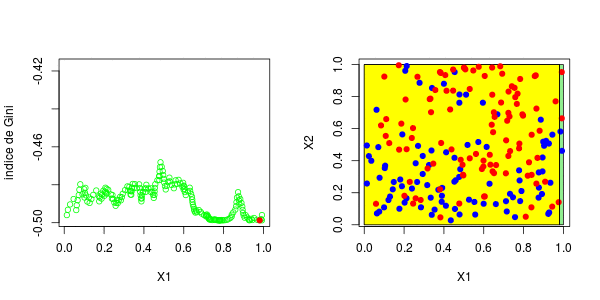
或者我们分割第二个分区(然后得到以下分区),
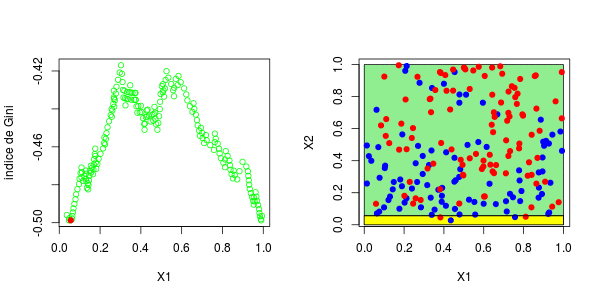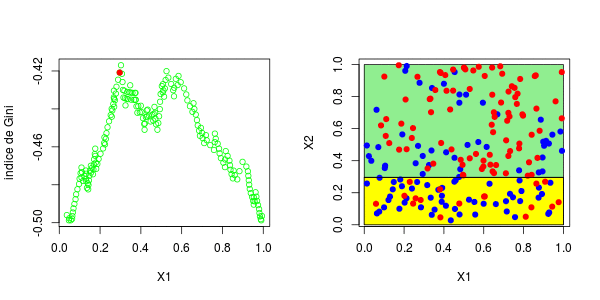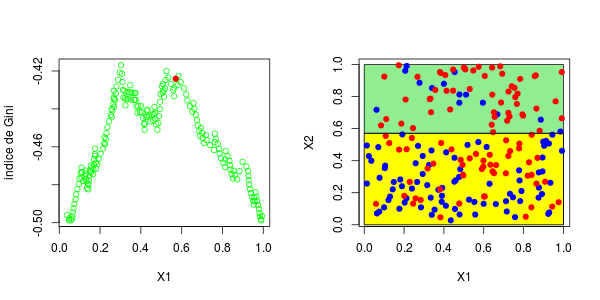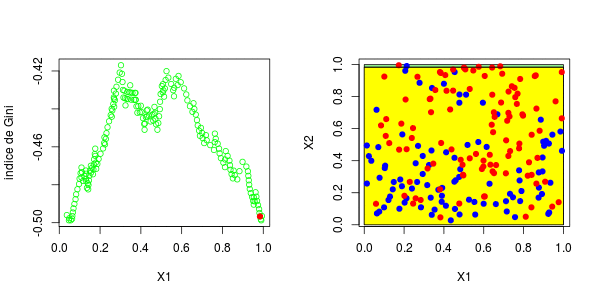
在这里,最好先分割第二个变量。实际上,我们回到了前面讨论的一维情况:正如预期的那样,最好在0.3左右进行分割。以下代码已确认这一点,
var n dev yval splits.cutleft splits.cutright
1 X2 200 49.875000 0.4750000 <0.302548 >0.302548
2 X1 69 12.811594 0.7536232 <0.800113 >0.800113
4 <leaf> 57 8.877193 0.8070175
5 <leaf> 12 3.000000 0.5000000对于第二个结,应考虑四种情况:在第二个变量上再次分裂(再次),在上一个结之上或之下(请参见左下方)或在第一个变量上分裂。然后在上一个结的下方或上方设置一个分区(请参见右下方),
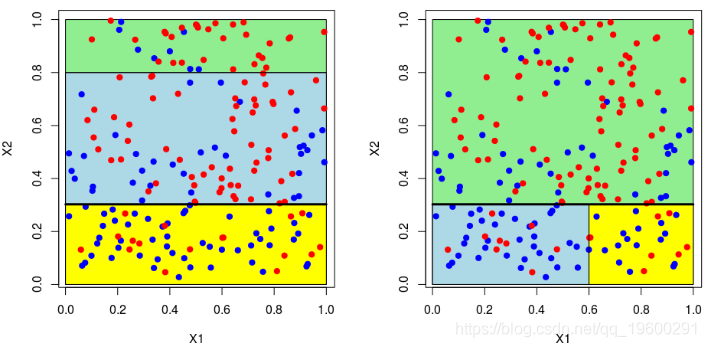
为了使树可视化,代码如下
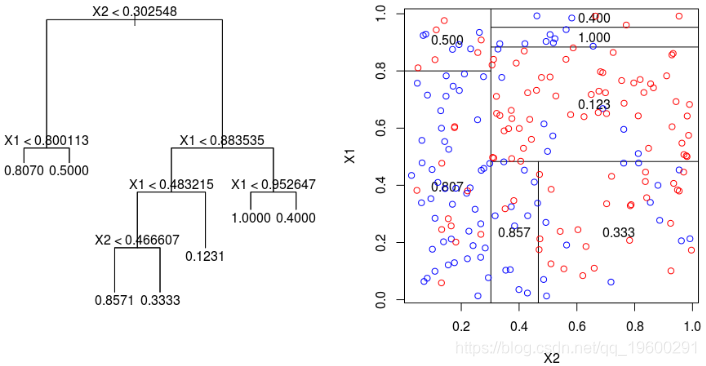
注意,我们也可以可视化该分区。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 Python古代文物成分分析与鉴别研究:灰色关联度、岭回归、K-means聚类、决策树分析
Python古代文物成分分析与鉴别研究:灰色关联度、岭回归、K-means聚类、决策树分析 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析


