
精度和查全率源自信息检索,但也用于机器学习设置中。
但是,在某些情况下,使用精度和查全率可能会出现问题。
可下载资源
在这篇文章中,我将讨论召回率和精确度的缺点,并说明为什么敏感性和特异性通常更有用。
定义
对于类别0和1的二进制分类问题,所得混淆矩阵具有以下结构:
| 预测/参考 | 1 | 0 |
|---|---|---|
| 1 | TP | FP |
| 0 | FN | TN |
其中TP表示真阳性的数量(模型正确预测阳性类别),FP表示假阳性的数量(模型错误预测阳性类别),FN表示假阴性的数量(模型错误预测阴性类别),TN表示真实否定数(模型正确预测否定类别)。敏感性(召回率),精确度(阳性预测值,PPV)和特异性(真阴性率,TNV)的定义如下:
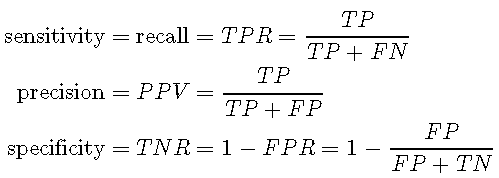

灵敏度确定正确预测来自阳性分类的观察结果的速率,而精度则表明正确预测预测的正确率。另一方面,特异性是基于假阳性的数量,它表示正确预测来自阴性类别的观察结果的速率。
敏感性和特异性的优势
基于敏感性和特异性的模型评估适用于大多数数据集,因为这些措施会考虑混淆矩阵中的所有条目。敏感性处理真假阳性和假阴性,而特异性处理假阳性和假阴性。这意味着当同时考虑真阳性和阴性时,敏感性和特异性的结合是一项整体措施。
敏感性和特异性可以用一个单一的量来概括,即平衡的准确度,其定义为两种方法的平均值:
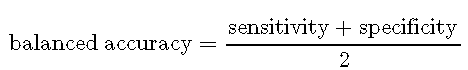

平衡精度在[0,1] [0,1]范围内,其中0和1的值分别表示最坏的分类器和最好的分类器。
召回率和精确度的缺点
使用召回率和精度评估模型不会使用混淆矩阵的所有单元。回忆处理的是真实的肯定和错误的否定,而精度处理的是真实的肯定和错误的肯定。因此,使用这对绩效衡量指标,就不会考虑真正的负面影响。因此,精度和召回率仅应在否定类别的正确识别不起作用的情况下使用。 可以将精度定义为
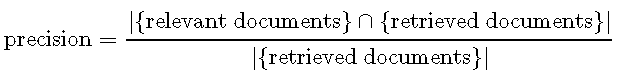

精度和召回率通常归纳为一个单一的数量,即F1得分 :
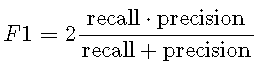

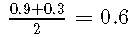

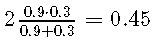

F1在[0,1] [0,1]范围内,对于分类器,将最大化精度和召回率,将为1。由于F1分数基于 平均值,因此对于精度和查全率的不同值非常敏感。假设分类器的灵敏度为90%,精度为30%。那么常规平均值将是,但是 平均值(F1得分)将是。
例子
在这里,我提供两个示例。第一个示例研究了将精度用作性能指标时可能出现的问题。
使用精度时会出什么问题?
当很少有观察结果属于肯定类别时,精度是一个特别糟糕的衡量标准。让我们假设一个临床数据集,其中90%90%的人患病(阳性),只有10%10%的人健康(阴性)。让我们假设我们已经开发了两种测试来对患者是疾病还是健康进行分类。两种测试的准确度均为80%,但会产生不同类型的错误。
# to use waffle, you need
# o FontAwesome
iron(
waffle(c("Diseased" = 90, "Healthy" = 10), rows = 5, use_glyph = "child",
glyph_size = 5, title = "Reference", colors = ref.colors),
waffle(c("Diseased (TP)" = 80, "Healthy (FN)" = 10, "Diseased (FP)" = 10),
rows = 5, use_glyph = "child",
glyph_size = 5, title = "Clinical Test 1", colors = c(true.colors[1], false.colors[2], false.colors[1]))
)
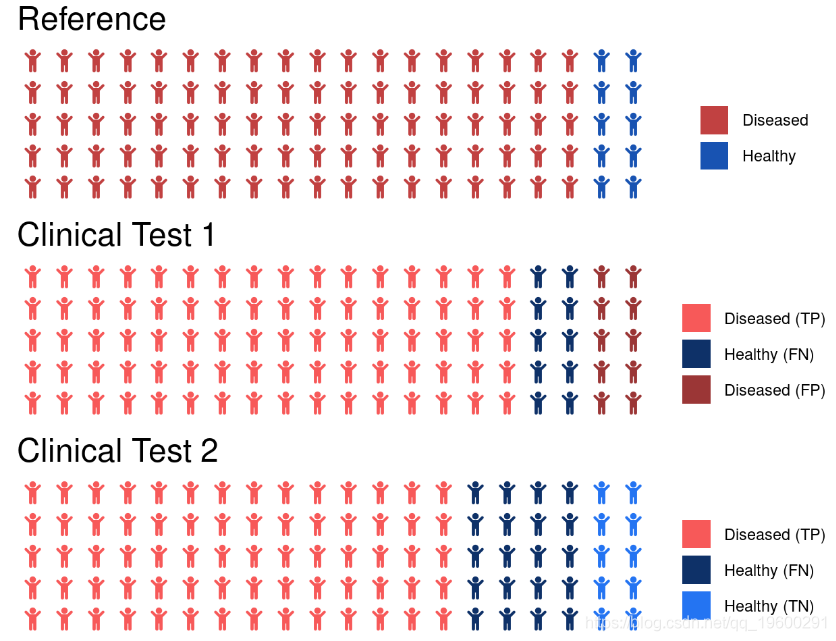

第一次测试的混淆矩阵
| 预测/参考 | 有病 | 健康 |
|---|---|---|
| 有病 | TP = 80 | FP = 10 |
| 健康 | FN = 10 | TN = 0 |
二次测试的混淆矩阵
| 预测/参考 | 有病 | 健康 |
|---|---|---|
| 有病 | TP = 70 | FP = 0 |
| 健康 | FN = 20 | TN = 10 |
两种测试的比较
让我们比较两个测试的性能:
| 测量 | 测试1 | 测试2 |
|---|---|---|
| 灵敏度(召回) | 88.9% | 77.7% |
| 特异性 | 0% | 100% |
| 精确 | 88.9% | 100% |
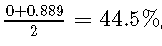

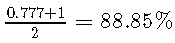

考虑到敏感性和特异性,我们不会选择第一个测试,因为它的平衡准确度仅为,而第二个测试的平衡准确度仅为 。
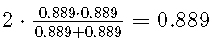

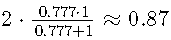

但是,使用精度和召回率,第一个测试的F1得分为,而第二个测试的得分更低,为。因此,尽管特异性为0%,但我们发现第一个测试优于第二个测试。因此,当使用该测试时, 所有健康患者将被分类为患病。这将是一个大问题,因为所有这些患者都会由于误诊而遭受严重的心理压力和昂贵的治疗。如果我们改用特异性,我们将选择第二种模型,该模型不会以竞争敏感性产生任何假阳性。
让我们考虑一个信息检索示例,以说明精度何时是有用的标准。假设我们要比较两种具有80%的准确性的文档检索算法。
iron(
waffle(c("Relevant" = 30, "Irrelevant" = 70), rows = 5, use_glyph = "file",
glyph_size = 5, title = "Reference", colors = ref.colors),
waffle(c("Relevant (TP)" = 25, "Irrelevant (FN)" = 5, "Relevant (FP)" = 15, "Irrelevant (TN)" = 55),
rows = 5, use_glyph = "file",
glyph_size = 5, title = "Retrieval Algorithm 1", colors = c(true.colors[1], false.colors[2], false.colors[1], true.colors[2]))
)
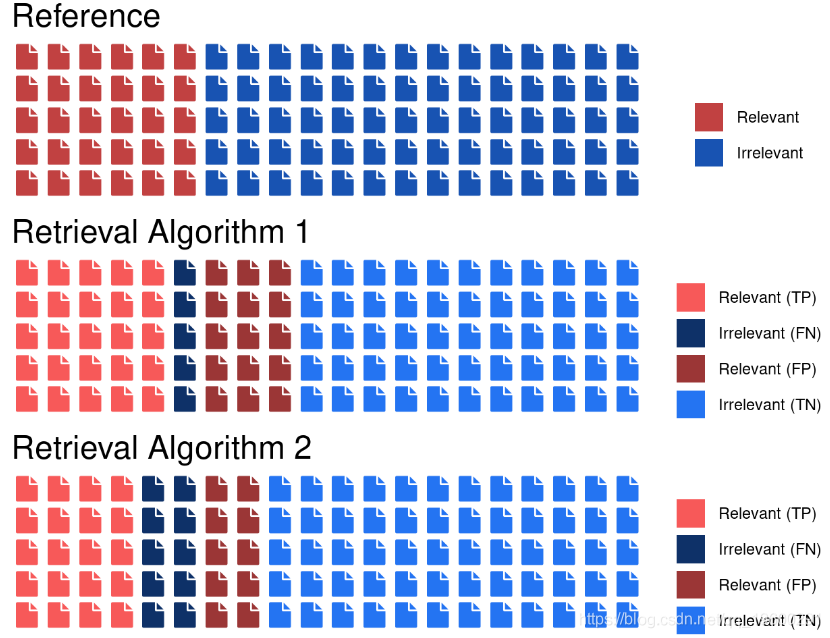

第一种算法的混淆矩阵
| 预测/参考 | 相关 | 不相关 |
|---|---|---|
| 相关 | TP = 25 | FP = 15 |
| 不相关 | FN = 5 | TN = 55 |
第二种算法的混淆矩阵
| 预测/参考 | 相关 | 不相关 |
|---|---|---|
| 相关 | TP = 20 | FP = 10 |
| 不相关 | FN = 10 | TN = 60 |
两种算法的比较
让我们根据混淆矩阵计算两种算法的性能:
| 测量 | 算法1 | 算法2 |
|---|---|---|
| 灵敏度(召回) | 83.3% | 66.7% |
| 特异性 | 78.6% | 85.7% |
| 精确 | 62.5% | 66.7% |
| 平衡精度 | 80.95% | 76.2% |
| F1分数 | 71.4% | 66.7% |
在此示例中,平衡的精度和F1分数都将导致首选第一种算法而不是第二种算法。请注意,报告的平衡精度绝对高于F1分数。这是因为由于来自否定类的大量丢弃观察,这两种算法的特异性都很高。由于F1分数不考虑真阴性的比率,因此精确度和召回度比敏感性和特异性更适合此任务。
摘要
在这篇文章中,我们看到应该仔细选择绩效指标。尽管敏感性和特异性通常表现良好,但精确度和召回率仅应在真正的阴性率不起作用的情况下使用。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据 【视频】因子分析简介及R语言应用实例:对地区经济研究分析重庆市经济指标
【视频】因子分析简介及R语言应用实例:对地区经济研究分析重庆市经济指标 R语言宏观经济学:IS-LM曲线可视化货币市场均衡
R语言宏观经济学:IS-LM曲线可视化货币市场均衡


