
在本文中,我们将在贝叶斯框架中引入回归建模,并使用PyMC3 MCMC库进行推理。
我们将首先回顾经典或概率论者的多重线性回归方法。然后我们将讨论贝叶斯如何考虑线性回归。
作者

可下载资源
用PyMC3进行贝叶斯线性回归
在本节中,我们将对统计实例进行一种历史悠久的方法,即模拟一些我们知道的属性的数据,然后拟合一个模型来恢复这些原始属性。
概要:
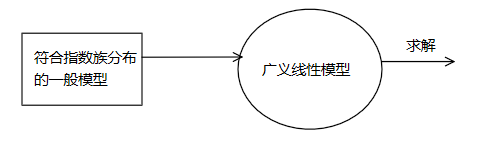
本文将会 说明 线性回归和逻辑回归都是广义线性模型的一种特殊形式,介绍广义线性模型的一般求解步骤。 利用广义线性模型推导 出 多分类的Softmax Regression。
线性回归中我们假设:
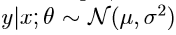
逻辑回归中我们假设:
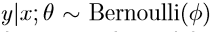
指数分布族( The exponential family)
首先我们定义一下什么是指数分布族,它有如下形式:
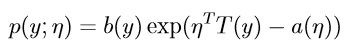
-
是 自然参数 ( natural parameter )
-
是充分统计量( sufficient statistic ) (一般情况下
)
-
是 log partition function (
充当正规化常量的角色,保证
)
也就是所 T,a, b 确定了一种分布, 是 该分布的参数。
选择合适的 T, a,b 我们可以得到 高斯分布 和 Bernoulli 分布。
Bernoulli分布的指数分布族形式:
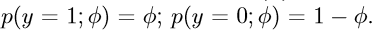
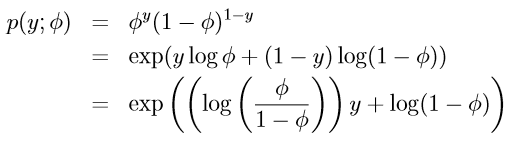
即:在如下参数下 广义线性模型是 Bernoulli 分布
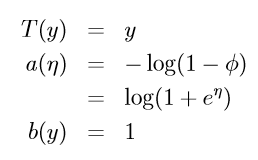
Gaussian 分布的指数分布族形式:
在线性回归中, 对于模型参数
的选择没有影响,为了推导方便我们将其设为1:
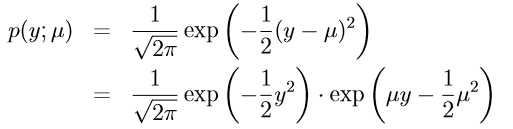
得到 对应的参数:
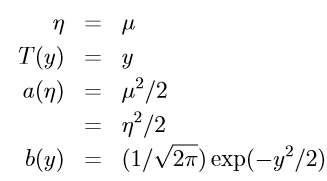
用广义线性模型进行建模:
想用 广义线性模型对一般问题进行建模首先需要明确几个 假设:
-
y的条件概率属于指数分布族
-
给定x 广义线性模型的目标是 求解
, 不过由于 很多情况下
所以我们的目标变成了
, 也即 我们希望拟合函数为
( 备注: 这个条件在 线性回归 和 逻辑回归中都满足, 例如 逻辑回归中
)
-
自然参数
与 x是线性关系 :
(
为向量时
)
有了如上假设 就可以 进行建模和求解了:
具体参考下面例子。
广义线性模型 推导出 线性回归:
step1:
step2: 由假设2 得到:

step1:
step2: 与上面同理
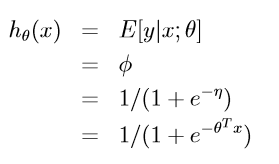
广义线性模型推导出 Softmax Regression (多分类算法 ):
【step1】:
y有多个可能的分类: ,
每种分类对应的概率: 但是 由于
, 所以一般 用 k-1个参数
其中
为了将 多项分布 表达为 指数族分布:
-
定义
,它不再是 一个数 而是一个变量
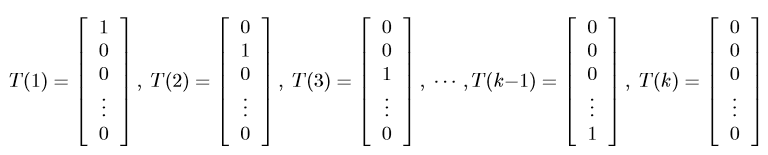
-
引进指示函数:
为
得到它的指数分布族形式 以及 各个对应参数为:
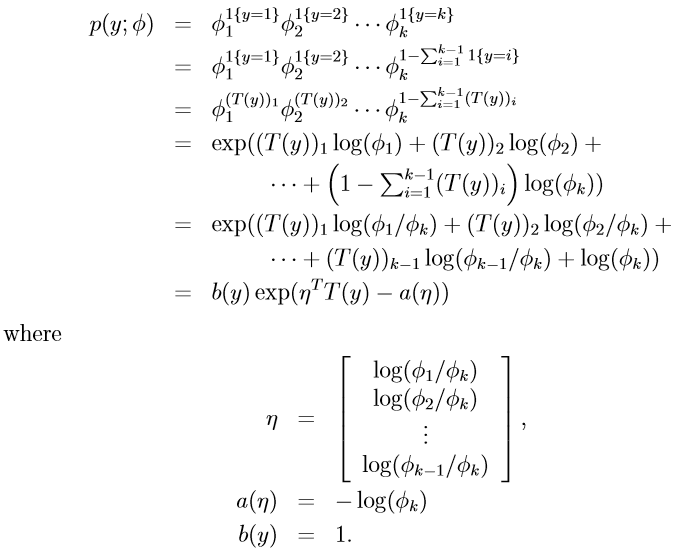
求出 :
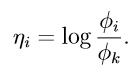
=>
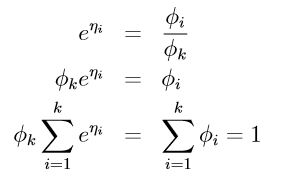
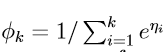
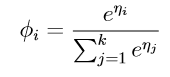
也即:

【step2】
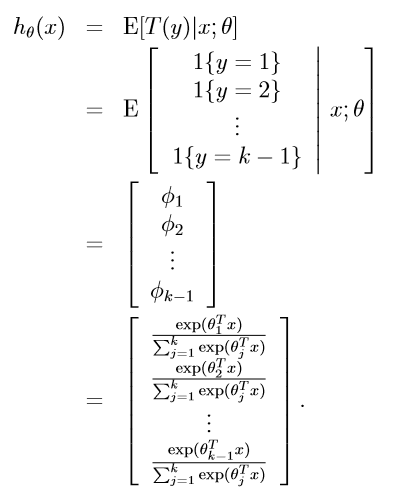
接下了只需要根据 最大似然法拟合参数即可:
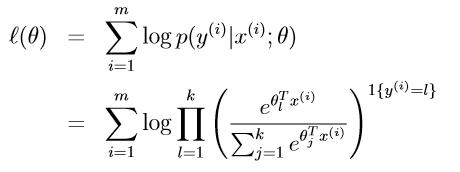
什么是广义线性模型?
在我们开始讨论贝叶斯线性回归之前,我想简要地概述广义线性模型(GLM)的概念,因为我们将使用它们来在PyMC3中制定我们的模型。
广义线性模型是将普通线性回归扩展到更一般形式的回归的灵活机制,包括逻辑回归(分类)和泊松回归(用于计数数据)以及线性回归本身。
GLM允许具有除正态分布以外的误差分布的响应变量(参见频率分区中的上述)。
用PyMC3模拟数据并拟合模型
在我们使用PyMC3来指定和采样贝叶斯模型之前,我们需要模拟一些噪声线性数据。
if __name__ == "__main__":
这些是我们的“真实”参数 beta_0 = 1.0 # 常数项
beta_1 = 2.0 # 斜率
# 模拟100个数据
N = 100
eps_sigma_sq = 0.5
# 模拟线性数据
df = simulate_linear_data(N, beta_0, beta_1, eps_sigma_sq)
#绘制数据,并进行线性回归拟合
#使用seaborn包
sns.lmplot(x="x", y="y", data=df, size=10)
plt.xlim(0.0, 1.0)输出如下图所示:
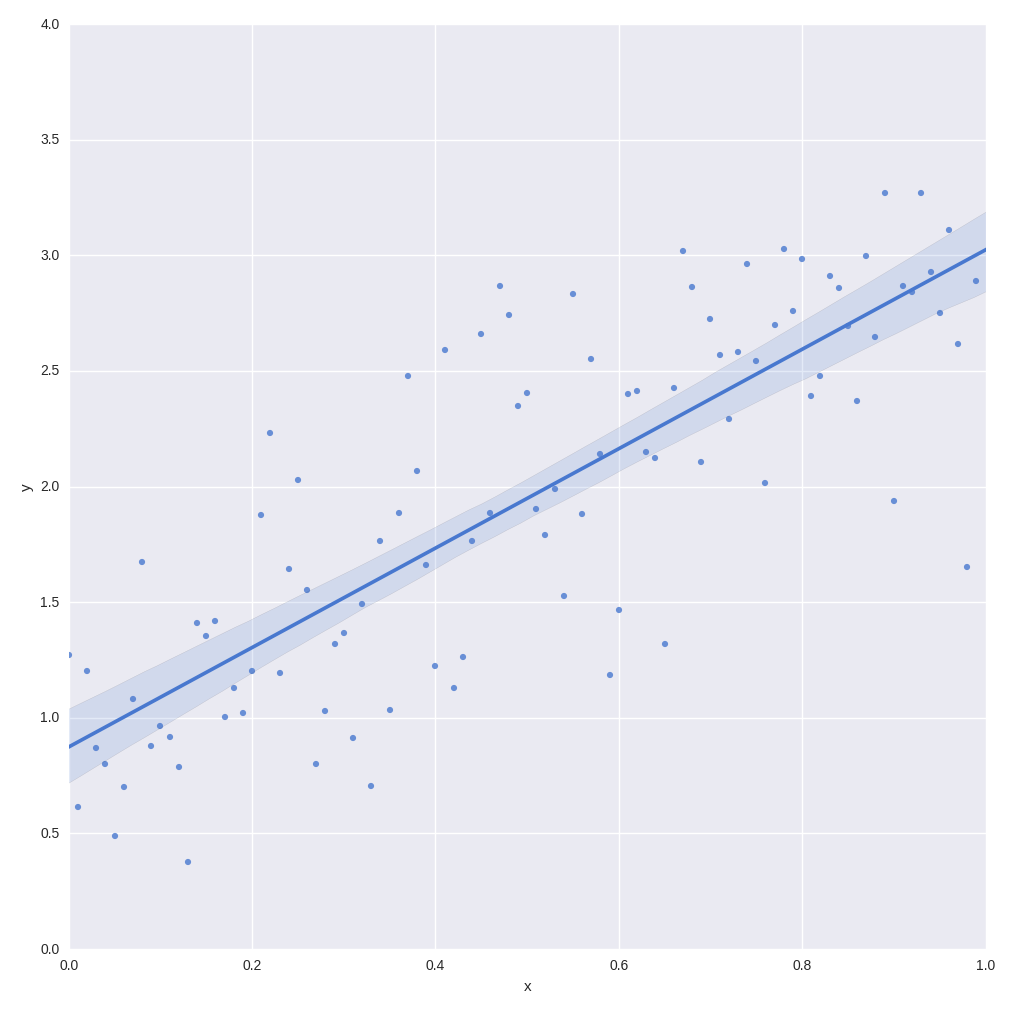
通过Numpy,pandas和seaborn模拟噪声线性数据
现在我们已经进行了模拟,我们想要对数据拟合贝叶斯线性回归。这是glm模块进来的地方。它使用与R指定模型类似的模型规范语法。
然后我们将找到MCMC采样器的最大后验概率(MAP)估计值。最后,我们将使用No-U-Turn Sampler(NUTS)来进行实际推理,然后绘制模型的曲线,将前500个样本丢弃为“burn in”。
Applied log-transform to sd and added transformed sd_log to model.
[---- 11% ] 563 of 5000 complete in 0.5 sec
[--------- 24% ] 1207 of 5000 complete in 1.0 sec
[-------------- 37% ] 1875 of 5000 complete in 1.5 sec
[-----------------51% ] 2561 of 5000 complete in 2.0 sec
[-----------------64%---- ] 3228 of 5000 complete in 2.5 sec
[-----------------78%--------- ] 3920 of 5000 complete in 3.0 sec
[-----------------91%-------------- ] 4595 of 5000 complete in 3.5 sec
[-----------------100%-----------------] 5000 of 5000 complete in 3.8 sectraceplot如下图所示:

使用PyMC3将贝叶斯GLM线性回归模型拟合到模拟数据
我们可以使用glm库调用的方法绘制这些线plot_posterior_predictive。该方法采用trace对象和plot(samples)的行数。
首先我们使用seaborn lmplot方法,这次fit_reg参数设置False为停止绘制频数回归曲线。然后我们绘制100个采样的后验预测回归线。最后,我们绘制使用原始的“真实”回归线和β1=2的参数。下面的代码片段产生了这样的情节:β0=1β0=1β1=2β1=2
我们可以在下图中看到回归线的抽样范围:


 【视频】N-Gram、逻辑回归反欺诈模型文本分析招聘网站欺诈可视化|附数据代码
【视频】N-Gram、逻辑回归反欺诈模型文本分析招聘网站欺诈可视化|附数据代码 R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验 R语言分类回归分析考研热现象分析与考研意愿价值变现
R语言分类回归分析考研热现象分析与考研意愿价值变现 R语言贝叶斯INLA空间自相关、混合效应、季节空间模型、SPDE、时空分析野生动物数据可视化
R语言贝叶斯INLA空间自相关、混合效应、季节空间模型、SPDE、时空分析野生动物数据可视化


