用户和产品的潜在特征编写推荐系统矩阵分解工作原理使用潜在表征来找到类似的产品。
我们可以通过为每个用户和每部电影分配属性，然后将它们相乘并合并结果来估计用户喜欢电影的程度。
可下载资源
1. 用户和产品的潜在特征
自动化推荐系统通常用于根据现有的偏好数据为用户提供他们感兴趣的产品建议。 文献中通常描述了不同类型的推荐系统。我们这篇文章将突出介绍两个主要类别，然后在第二个类别上进一步扩展：
基于内容的过滤：这些过滤器利用用户偏好来做出新的预测。 当用户提供有关其偏好的明确信息时，系统会记录并使用这些信息来自动提出建议。 我们日常使用的许多网站和社交媒体都属于此类。
协同过滤：当用户提供的信息不足以提出项目建议时，会发生什么情况？ 在这些情况下，我们可以使用其他用户提供的具有相似首选项的数据。 此类别中的方法利用了一组用户的过去选择历史来得出建议。
在第一种情况下，期望给定的用户建立一个清楚表明偏好的配置文件，在第二种情况下，此信息可能无法完全使用，但是我们希望我们的系统仍能够基于类似的证据提出建议 用户提供。 一种称为概率矩阵分解的方法（简称为PMF）通常用于协同过滤，并且将成为本文其余部分讨论的主题。 现在让我们深入研究此算法的细节及其直觉。
概率矩阵分解解释
假设我们有一组用户u1，u2，u3…uN，他们对一组项目v1，v2，v3…vM进行评分。 然后，我们可以将评分构建为N行和M列的矩阵R，其中N是用户数，M是要评分的项目数。
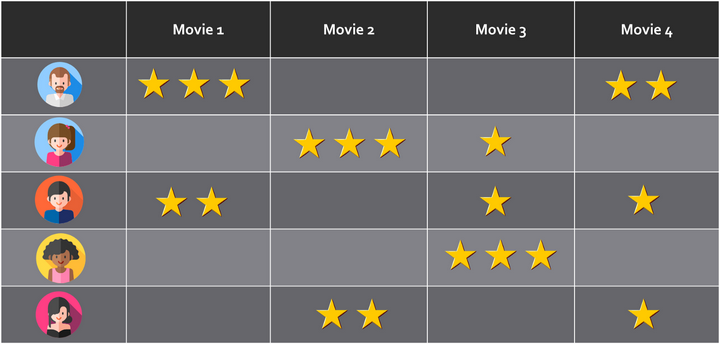
评分映射。 可以将其视为每个用户（行）对多个项目（列）进行评分的矩阵
R矩阵的一个重要特征是它是稀疏的。 也就是说，仅其某些单元格具有非空的评级值，而其他单元格则没有。 对于给定的用户A，系统应该能够基于他/她的偏好以及类似用户的选择来提供项目推荐。 但是，用户A不必明确推荐某项就可以对其进行推荐。 具有相似首选项的其他用户将弥补有关用户A的缺失数据。这就是为什么概率矩阵分解属于协同过滤推荐系统的类别。
让我们考虑一下电影推荐系统。 想象一下，如果我们被要求观看和评价特定季节中放映的每部电影会是什么样子。 那是不切实际的，不是吗？ 我们根本没有时间这样做。
鉴于并非所有用户都能够对所有可用项目进行评分，我们必须找到一种方法来填补R矩阵的信息空白，并且仍然能够提供相关建议。 PMF通过利用类似用户提供的评级来解决此问题。 从技术上讲，它利用了贝叶斯学习的一些原理，这些原理也适用于我们缺少或不完整数据的其他情况。
可以通过使用两个低阶矩阵U和V来估计R矩阵，如下所示：
此处，UT是一个NxD矩阵，其中N是注册用户数，D是等级。 V是DxM矩阵，其中M是要评估的项目数。 因此，NxM评级矩阵R可以通过以下方式近似：
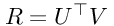
公式1：R表达式
从现在开始，我们的工作是找到UT和V，它们将反过来成为模型的参数。 因为U和V是低阶矩阵，所以PMF也被称为低阶矩阵分解问题。 此外，U和V矩阵的这一特殊特征使得PMF甚至对于包含数百万条记录的数据集也可扩展。
PMF从贝叶斯学习中得出的直觉用于参数估计。 一般而言，我们可以说在贝叶斯推断中，我们的目的是借助贝叶斯规则来找到模型参数的后验分布：
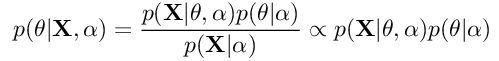
公式2：参数的贝叶斯规则
在这里，X是我们的数据集，θ是分布的参数或参数集。 α是分布的超参数。 p（θ| X，α）是后验分布，也称为后验分布。 p（X |θ，α）是似然，p（θ|α）是先验。 训练过程的整体思路是，随着我们获得有关数据分布的更多信息，我们将调整模型参数θ以适合数据。 从技术上讲，后验分布的参数将插入到先前的分布中，以进行训练过程的下一次迭代。 也就是说，给定训练步骤的后验分布最终将成为下一步骤的先验。 重复该过程，直到步骤之间的后验分布p（θ| X，α）几乎没有变化为止。
现在，让我们回到有关PMF的直觉上。 如前所述，我们的模型参数将是U和V，而R将是我们的数据集。 经过培训后，我们将得到一个修订的R *矩阵，该矩阵还将包含对用户项目单元格最初在R中为空的评分。我们将使用此修订的评分矩阵进行预测。 基于这些考虑，我们将拥有：
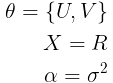
其中σ是零均值球形高斯分布的标准偏差。 然后，通过替换等式2中的这些表达式，我们将得到：
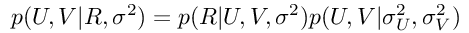
由于U和V矩阵彼此独立（用户和项独立发生），因此该表达式也可以这样写：
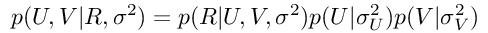
公式3：PMF的A-Posteriori分布
现在是时候找出该方程式的每个分量了。 首先，似然函数由下式给出：
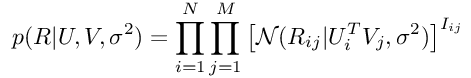
公式4：观测等级的分布
在此，I {ij}是一个指标，当第i行和第j列的评级存在时，其值为1，否则为0。 如我们所见，此分布是具有以下参数的spherical Gaussian分布：
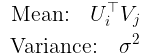
反过来，U和V的先验分布由下式给出：
公式5和6：U和V的先验分布
这是两个零均值球面高斯（spherical Gaussians）。 然后，通过在3中替换4、5和6，我们将得到：
为了训练我们的模型，我们将寻求通过将参数U和V的导数等价为零来最大化此函数。 但是，由于高斯函数中的exp函数，这样做将非常困难。 为了克服这个问题，我们应该将对数应用于前面的方程式的两边，然后应用所需的导数。 因此，通过将对数应用于上一个方程的两边，我们将获得：
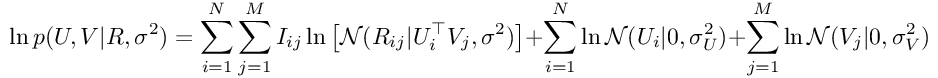
这是一个更容易区分的表达方式。 我们也知道，根据定义，高斯PDF由以下公式给出：
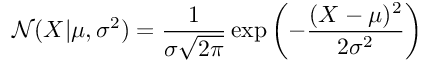
因此，我们对数后验的表达式将如下所示（注意：为简单起见，我们已删除了常量）：
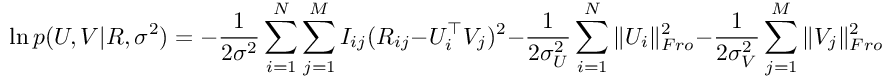
Fro后缀表示Frobenius范数，它由下式给出：
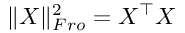
最后，通过引入一些附加的符号来标识模型的超参数，我们将获得：
公式7：PMF的对数后验
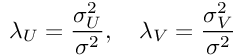
然后，通过对参数微分方程式7并将导数等于零，我们将得到：
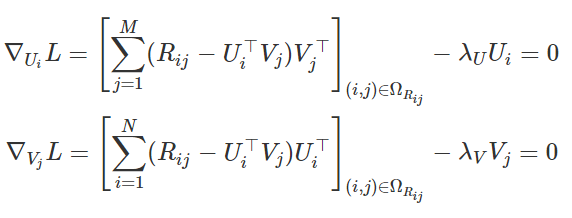
从这里，我们可以导出表达式以更新Ui和Vj：
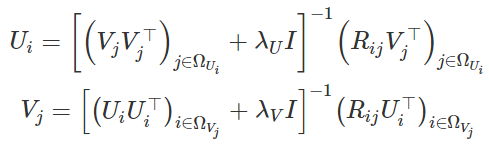
公式8和9：用于更新U和V的表达式
假设λU和λV都不为零，则可以保证所涉及的逆矩阵存在。 作为训练过程的一部分，我们将迭代更新Ui和Vj。 一旦找到最佳值，就可以使用方程式7获得log-MAP的值（最大后验值）。正如我们在Python实现中所看到的那样，我们可以使用该值来监控训练收敛 。
相同的计算可以表示为矩阵乘法问题。首先，我们把用户属性放在一个名为U的矩阵中，在这个例子中是5，-2，1，-5和5。然后，我们把电影属性放在一个名为M的矩阵中，我们使用矩阵乘法来找出用户的评分。
但要做到这一点，我们必须已经知道用户属性和电影属性。为每个用户和每部电影提供属性评级并不容易。我们需要找到一种自动的方法。我们来看看电影评分矩阵，
它显示了我们数据集中的所有用户如何评价电影。这个矩阵非常稀疏，但它给了我们很多信息。例如，我们知道用户ID2给电影1号五颗星。所以，基于此，我们可以猜测，这个用户的属性可能类似于电影的属性，因为它们匹配的很好。换句话说，我们有一些线索可以使用。
让我们看看我们如何利用这些线索来了解每部电影和每个用户。在我们刚刚看到的等式中，U乘M等于电影等级，我们已经知道一些用户的实际电影等级。我们已经拥有的电影评分矩阵是我们方程式的解决方案。虽然它是解决方案的一部分，但是这个阵列仍然有很多漏洞，但对于我们来说，这已经足够了。
实际上，我们可以使用目前为止我们所知道的电影评级，然后逆向找到满足该等式的U矩阵和M矩阵。当然，这才是最酷的部分。当我们将U和M相乘时，他们实际上会给我们一个完整的矩阵，我们可以使用那个完成的矩阵来推荐电影。
让我们回顾一下我们将如何构建这个推荐系统。
首先，我们创建了我们在数据集中所有用户评论的矩阵。接下来，我们从已知的评论中分解出一个U矩阵和一个M矩阵。最后，我们将把我们找到的U和M矩阵相乘，得到每个用户和每部电影的评分。但是还有一个问题。以前，当我们为每个用户和每部电影手工创建属性时，我们知道每个属性的含义。我们知道第一个属性代表动作，第二个代表剧情，等等。但是当我们使用矩阵分解来提出U和M时，我们不知道每个值是什么意思。我们所知道的是，每个价值都代表了一些让用户感觉被某些电影吸引的特征。我们不知道如何用文字来描述这些特征。因此，U和M被称为潜在向量。潜在的词意味着隐藏。换句话说，这些向量是隐藏的信息，我们通过查看评论数据和反向推导。
2. 编写推荐系统
我们来编写推荐系统的主要代码。打开Chapter 5/factor_review_matrix.py。首先，我将使用pandas read_csv函数将检查数据集加载到名为raw_dataset_df的数据集中。
raw_dataset_df = pd.read_csv('movie_ratings_data_set.csv')然后我们使用pandas数据透视表函数来构建评论矩阵。在这一点上，ratings_df包含一个稀疏的评论阵列。
ratings_df = pd.pivot_table(raw_dataset_df, index='user_id', columns='movie_id', aggfunc=np.max)
接下来，我们希望将数组分解以找到用户属性矩阵和我们可以重新乘回的电影属性矩阵来重新创建收视率数据。为此，我们将使用低秩矩阵分解算法。我已经在matrix_factorization_utilities.py中包含了这个实现。我们将在下一个视频中详细讨论它是如何工作的，但让我们继续使用它。首先，我们传递了评分数据，但是我们将调用pandas的as_matrix()函数，以确保我们作为一个numpy矩阵数据类型传入。
接下来，这个方法接受一个名为num_features的参数。
Num_features控制为每个用户和每个电影生成多少个潜在特征。我们将以15为起点。这个函数还有个参数regularization_amount。现在让我们传入0.1。在后面的文章中我们将讨论如何调整这个参数。
函数的结果是U矩阵和M矩阵，每个用户和每个电影分别具有15个属性。现在，我们可以通过将U和M相乘来得到每部电影的评分。但不是使用常规的乘法运算符，而是使用numpy的matmul函数，所以它知道我们要做矩阵乘法。
随时关注您喜欢的主题
结果存储在一个名为predicted_ratings的数组中。最后，我们将predict_ratings保存到一个csv文件。
首先，我们将创建一个新的pandas数据框来保存数据。对于这个数据框，我们会告诉pandas使用与ratings_df数据框中相同的行和列名称。然后，我们将使用pandas csv函数将数据保存到文件。运行这个程序后可以看到，它创建了一个名为predicted_ratings.csv的新文件。我们可以使用任何电子表格应用程序打开该文件。
这个数据看起来就像我们原来的评论数据，现在每个单元格都填满了。现在我们评估下每个单个用户会为每个单独的电影评分。例如，我们可以看到用户3评级电影4，他们会给它一个四星级的评级。现在我们知道所有这些评分，我们可以按照评分顺序向用户推荐电影。让我们看看用户1号，看看我们推荐给他们的电影。在所有这些电影中，如果我们排除了用户以前评价过的电影，右边34号电影是最高分的电影，所以这是我们应该推荐给这个用户的第一部电影。当用户观看这部电影时，我们会要求他们评分。如果他们的评价与我们预测的不一致，我们将添加新评级并重新计算此矩阵。这将有助于我们提高整体评分。我们从中获得的评分越多，我们的评分阵列中就会出现的孔越少，我们就有更好的机会为U和M矩阵提供准确的值。
因为评分矩阵等于将用户属性矩阵乘以电影属性矩阵的结果，所以我们可以使用矩阵分解反向工作以找到U和M的值。
3. 矩阵分解工作原理
在代码中，我们使用称为低秩矩阵分解的算法，去做这个。我们来看看这个算法是如何工作的。矩阵分解是一个大矩阵可以分解成更小的矩阵的思想。所以，假设我们有一个大的数字矩阵，并且假设我们想要找到两个更小的矩阵相乘来产生那个大的矩阵，我们的目标是找到两个更小的矩阵来满足这个要求。如果您碰巧是线性代数的专家，您可能知道有一些标准的方法来对矩阵进行因式分解，比如使用一个称为奇异值分解的过程。但是，这是有这么一个特殊的情况下，将无法正常工作。问题是我们只知道大矩阵中的一些值。大矩阵中的许多条目是空白的，或者用户还没有检查特定的电影。所以，我们不是直接将评级数组分成两个较小的矩阵，而是使用迭代算法估计较小的矩阵的值。我们会猜测和检查，直到我们接近正确的答案。哎哎等等， 咋回事呢？首先，我们将创建U和M矩阵，但将所有值设置为随机数。因为U和M都是随机数，所以如果我们现在乘以U和M，结果是随机的。下一步是检查我们的计算评级矩阵与真实评级矩阵与U和M的当前值有多不同。但是我们将忽略评级矩阵中所有没有数据的点，只看在我们有实际用户评论的地方。我们将这种差异称为成本。成本就是错误率。接下来，我们将使用数字优化算法来搜索最小成本。数值优化算法将一次调整U和M中的数字。目标是让每一步的成本函数更接近于零。我们将使用的函数称为fmin_cg。
它搜索使函数返回最小可能输出的输入。它由SciPy库提供。最后，fmin_cg函数将循环数百次，直到我们得到尽可能小的代价。当成本函数的价值如我们所能得到的那样低，那么U和M的最终值就是我们将要使用的。但是因为它们只是近似值，所以它们不会完全完美。当我们将这些U矩阵和M矩阵相乘来计算电影评级时，将其与原始电影评级进行比较，我们会看到还是有一些差异。但是只要我们接近，少量的差异就无关紧要了。
4. 使用潜在特征来找到类似的产品
搜索引擎是用户发现新网站的常用方式。当第一次用户从搜索引擎访问您的网站时，您对用户尚不足以提供个性化推荐，直到用户输入一些产品评论时，我们的推荐系统还不能推荐他们。在这种情况下，我们可以向用户展示与他们已经在查看的产品类似的产品。目标是让他们在网站上，让他们看更多的产品。你可能在网上购物网站上看到过这个功能，如果你喜欢这个产品，你可能也会喜欢这些其他的产品。通过使用矩阵分解计算产品属性，我们可以计算产品相似度。让我们来看看find_similar_products.py。首先，我们将使用pandas的读取CSV功能加载电影评级数据集。
我们还会使用read_csv将movies.csv加载到名为movies_df的数据框中。
然后，我们将使用pandas的数据透视表函数(pivot_table)来创建评分矩阵，我们将使用矩阵分解来计算U和M矩阵。现在，每个电影都由矩阵中的一列表示。首先，我们使用numpy的转置函数来触发矩阵，使每一列变成一行。
M = np.transpose(M)这只是使数据更容易处理，它不会改变数据本身。在矩阵中，每个电影有15个唯一的值代表该电影的特征。这意味着其他电影几乎相同的电影应该是非常相似的。要找到类似这个电影的其他电影，我们只需要找到其他电影的编号是最接近这部电影的数字。这只是一个减法问题。让我们选择用户正在看的主要电影，让我们选择电影ID5。
movie_id = 5
movie_information = movies_df.loc[movie_id]我们可以通过查看movies_df数据框并使用pandas的loc函数通过其索引查找行来做到这一点。让我们打印出该电影的标题和流派。
print("We are finding movies similar to this movie:")
print("Movie title: {}".format(movie_information.title))
print("Genre: {}".format(movie_information.genre))接下来，让我们从矩阵中获取电影ID为5的电影属性。我们必须在这里减去一个，因为M是0索引，但电影ID从1开始。现在，让我们打印出这些电影属性，以便我们看到它们，这些属性我们准备好找到类似的电影。
如果你喜欢，你可以选择其他的电影。现在，我们来看看电影ID5的标题和流派。
第一步是从其他电影中减去这部电影的属性。这一行代码从矩阵的每一行中分别减去当前的电影特征。这给了我们当前电影和数据库中其他电影之间的分数差异。您也可以使用四个循环来一次减去一个电影，但使用numpy，我们可以在一行代码中完成。第二步是取我们在第一步计算出的差值的绝对值，numpy的ABS函数给我们绝对值，这只是确保任何负数出来都是正值。接下来，我们将每个电影的15个单独的属性差异合并为一个电影的总差异分数。 numpy的总和功能将做到这一点。我们还会传入访问权限等于一个来告诉numpy总结每行中的所有数字，并为每行产生一个单独的总和。在这一点上，我们完成了计算。我们只是将计算得分保存回电影列表中，以便我们能够打印每部电影的名称。在第五步中，我们按照我们计算的差异分数对电影列表进行排序，以便在列表中首先显示最少的不同电影。这里pandas提供了一个方便的排序值函数。最后，在第六步中，我们打印排序列表中的前五个电影。这些是与当前电影最相似的电影。
好的，我们来运行这个程序。 我们可以看到我们为这部电影计算的15个属性。这是我们发现的五个最相似的电影。第一部电影是用户已经看过的电影。 接下来的四部电影是我们向用户展示的类似项目。根据他们的头衔，这些电影看起来可能非常相似。他们似乎都是关于犯罪和调查的电影。续集，大城市法官三，都在名单上。这是用户可能也会感兴趣的电影。您可以更改电影ID并再次运行该程序，以查看与其他电影类似的内容。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
银行信贷风控专题：Python、R 语言机器学习数据挖掘应用实例合集：xgboost、决策树、随机森林、贝叶斯等
深度神经网络DNN、RNN、RCNN及多种机器学习金融交易策略研究|附数据代码
R语言混合SVD模型IBCF协同过滤推荐算法研究——以母婴购物平台为例
