时间序列(从现在起称为TS)被认为是数据科学领域中鲜为人知的技能之一。
视频
在Python和R语言中建立EWMA,ARIMA模型预测时间序列
本文学习创建时间序列预测的步骤,关注Dickey-Fuller检验、指数加权平均(EWMA)和ARIMA(自回归移动平均)模型,从理论上学习这些概念以及它们在python和R中的实现。
介绍
时间序列(从现在起称为TS)被认为是数据科学领域中鲜为人知的技能之一。
使用python创建时间序列预测
我们使用以下步骤:
- 时间序列是什么
- 加载和处理时间序列
- 如何检验时间序列的平稳性?
- 如何使时间序列平稳?
- 预测时间序列
1.什么是时间序列?
顾名思义,TS是以固定时间间隔收集的数据点的集合。
对这些数据进行分析,以确定长期趋势,从而预测未来或进行其他形式的分析。
但是什么使TS不同于常规回归问题呢?
- 它取决于时间。所以线性回归模型的基本假设,即观测值是独立的,在这种情况下不成立。
- 随着一个增加或减少的趋势,大多数TS具有某种形式的季节性趋势,即特定于特定时间范围的变化。例如,如果你看到一件羊毛夹克的销售随着时间的推移,你一定会发现冬季的销售量更高。
由于其固有的特性,对其进行分析涉及到各种步骤。下面将详细讨论这些问题。让我们从在Python中加载一个TS对象开始。我们使用航空乘客数据。
2加载和处理时间序列
Pandas有专门的库来处理TS对象,特别是datatime64[ns]类,它存储时间信息,我们可以快速执行一些操作。让我们从启动所需的库开始:
%matplotlib inline
from matplotlib.pylab import rcParams
data = pd.read_csv('AirPassengers.csv', parse_dates=['Month'], index_col='Month') 让我们逐一理解这些论点:
- parse dates:指定包含日期时间信息的列。如上所述,列名是’Month’。
- index_col:将Pandas用于TS数据背后的一个关键思想是,索引必须是描述日期时间信息的变量。所以这个参数告诉panda使用’Month’列作为索引。
- date parse:指定一个函数,将输入字符串转换为datetime变量。默认情况下,读取格式为“YYYY-MM-DD HH:MM:SS”的数据。如果数据不是此格式,则必须手动定义格式。类似于这里定义的dataparse函数的东西可以用于此目的。
现在我们可以看到数据以time对象作为索引,#Passengers作为列。我们可以使用以下命令交叉检查索引的数据类型:
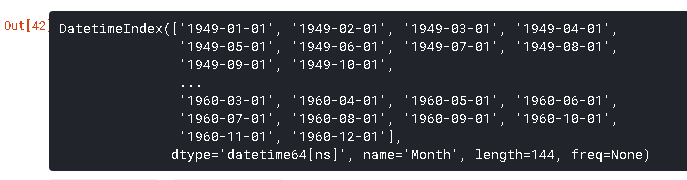
注意dtype=’datetime[ns]’确认它是一个datetime对象。作为个人偏好,我会将列转换为Series对象,以防止每次使用TS时都引用列名称。
ts = data[‘#Passengers’] ts.head(10) 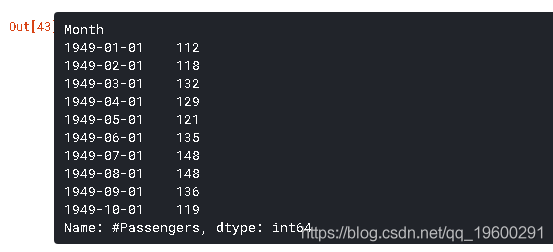
在进一步讨论之前,我将讨论一些TS数据的索引技术。让我们从选择Series对象中的特定值开始。这可以通过以下两种方式实现:
#1.指定索引为字符串常量:
ts['1949-01-01']
#2.导入datetime库并使用'datetime'函数:
from datetime import datetime 两者都将返回值“112”,这也可以从以前的输出中确认。假设我们想要1949年5月之前的所有数据。这可以通过两种方式实现:
#1. 指定整个范围:
ts['1949-01-01':'1949-05-01']
#2. 如果其中一个索引位于末尾,请使用“:”:
ts[:'1949-05-01']两者都将产生以下输出:
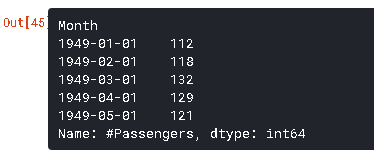
这里有两点需要注意:
- 与数字索引不同的是,结束索引包含在这里。例如,如果我们将列表索引为[:5],那么它将返回索引处的值–[0,1,2,3,4]。但这里的索引“1949-05-01”包含在输出中。
- 必须对索引进行排序,才能使范围发挥作用。
考虑另一个需要1949年所有值的例子。这可以通过以下方式实现:
随时关注您喜欢的主题
ts['1949'] 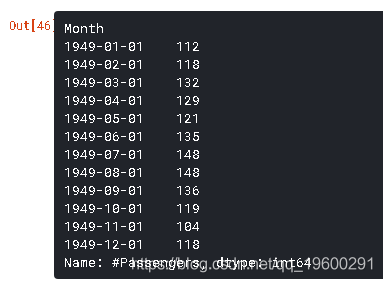
月份部分被省略了。类似地,如果您选择某个月的所有日期,则可以省略日期部分。
现在,让我们继续分析TS。
3.如何检验时间序列的平稳性?
如果TS的统计特性(如均值、方差)随时间保持不变,则称其为平稳的。但为什么重要呢?大多数TS模型都假设TS是平稳的。直觉上,我们可以假设,如果一个TS在一段时间内有一个特定的行为,那么它很有可能在将来也会有同样的行为。与非平稳序列相比,平稳序列的相关理论更为成熟和易于实现。
平稳性是使用非常严格的标准来定义的。然而,出于实际目的,我们可以假设序列是平稳的,如果它随时间具有恒定的统计特性,即:
- 恒定平均值
- 恒定方差
- 不依赖于时间的自协方差。
我将跳过这些细节,因为在本文中对其进行了非常明确的定义。让我们开始测试平稳性的方法。首先也是最重要的是简单地绘制数据并进行可视化分析。可以使用以下命令绘制数据:
plt.plot(ts) 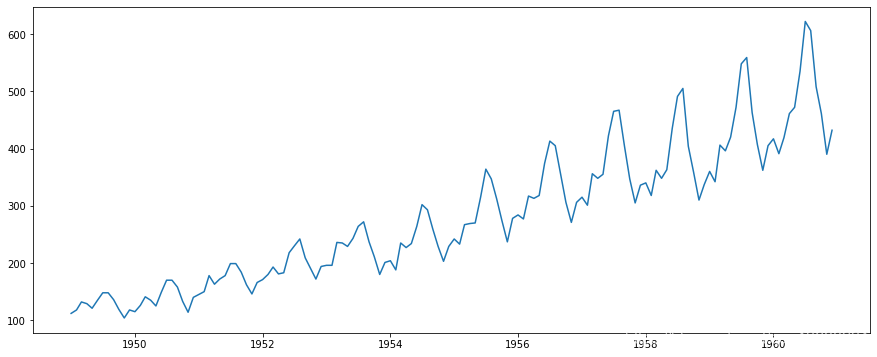
很明显,随着一些季节性变化,数据总体呈上升趋势。然而,可能并不总是能够做出这样的视觉直观推断(我们稍后会看到这样的情况)。因此,更正式地说,我们可以使用以下方法检查平稳性:
- 绘制滚动统计:我们可以绘制移动平均值或移动方差,看它是否随时间变化。移动平均值/方差,我的意思是,在任何时刻‘t’,我们将取去年的平均值/方差,即过去12个月的平均值/方差。但这更像是一种视觉技术。
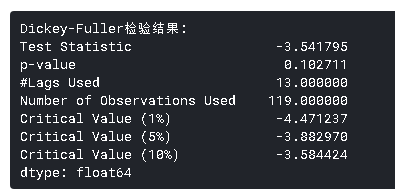
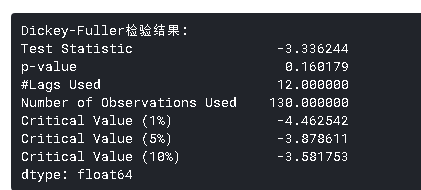
- Dickey-Fuller检验:这是检验平稳性的统计检验之一。这里的零假设是TS是非平稳的。检验结果包括检验统计量和不同置信水平的一些临界值。如果“检验统计量”小于“临界值”,我们可以拒绝零假设并说序列是平稳的。
在这一点上,这些概念听起来可能不是很直观。
回到平稳性检查,我们将使用滚动统计图以及Dickey-Fuller检验结果很多,所以我定义了一个函数,它以TS作为输入并为我们生成它们。
请注意,我绘制了标准差而不是方差,以保持单位与平均值相似。
def test_stat(timeseries):
orig = plt.plot(timeseries, color='blue',label='原始序列')
mean = plt.plot(rolmean, color='red', label='滚动平均')
std = plt.plot(rolstd, color='black', label = '滚动标准差')
plt.title('滚动平均数和标准偏差',fontproperties=myfont)
#执行Dickey-Fumer 检验:
dftest = adfuller(timeseries, maxlag=13, regression='ctt', autolag='BIC') 让我们为输入序列运行它:
test_stat(ts) 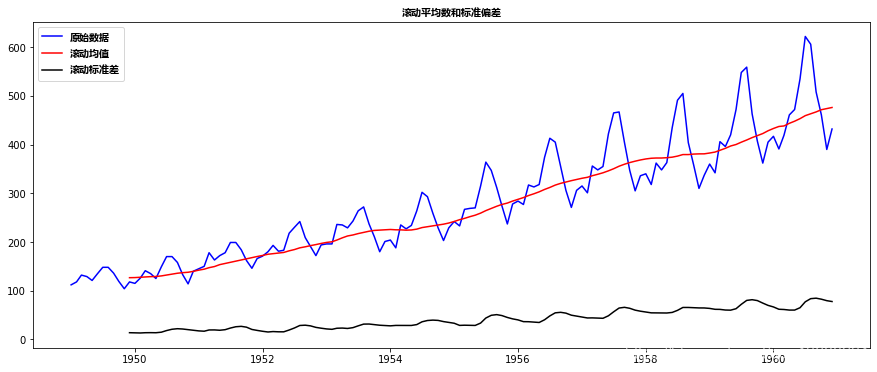
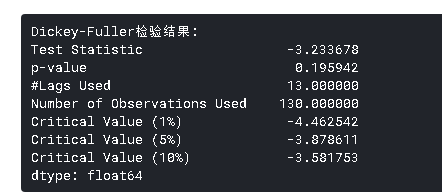
虽然标准差的变化很小,但平均值明显随时间增加,这不是一个平稳序列。而且,检验统计量远大于临界值。请注意,应该比较有符号的值,而不是绝对值。
下一步,我们将讨论可以用来将这个TS转换平稳的方法。
4如何使时间序列平稳?
虽然许多TS模型都采用平稳性假设,但实际时间序列中几乎没有一个是平稳的。统计学家们已经找到了使序列平稳的方法,我们现在就来讨论。实际上,要使一个序列完全平稳几乎是不可能的,但我们要尽量接近它。
让我们了解是什么使TS不稳定。TS的非平稳性有两个主要原因:
- 趋势-随时间变化的平均值。例如,在这个例子中,我们看到平均而言,乘客人数随着时间的推移而增长。
- 季节性-特定时间范围内的变化。由于加薪或节日的原因,人们可能有在特定月份出现的倾向。
其基本原理是对序列中的趋势和季节性进行建模或估计,并从序列中去除这些趋势和季节性以得到平稳序列。然后统计预测技术就可以在这个序列上实现。最后一步是通过应用趋势和季节性约束将预测值转换为原始规模。
注意:我将讨论一些方法。在这种情况下,有些可能工作得很好,而有些可能不行。但我们的想法是掌握所有的方法,而不是只关注手头的问题。
让我们从趋势部分开始。
估计和消除趋势
减少趋势的第一个技巧之一可以转换。例如,在这种情况下,我们可以清楚地看到存在显着的增长趋势。因此,我们可以应用转换,以惩罚更高的值,而不是较小的值。这些可以取对数,平方根,立方根等。在此处取对数转换简便简单:
np.log(ts) 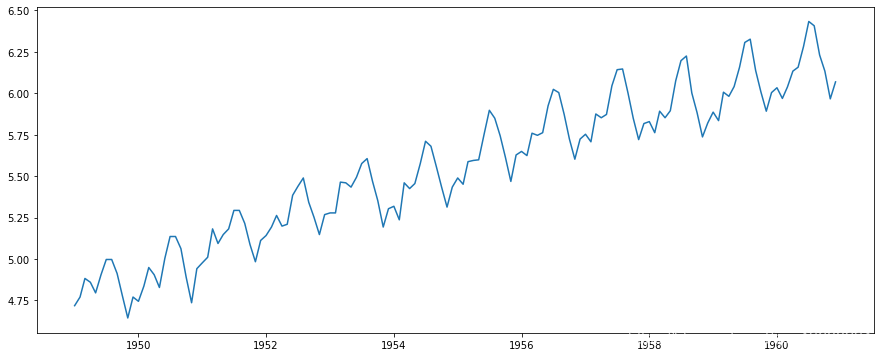
在这种简单的情况下,很容易看到数据的未来趋势。但在有噪音的情况下,它不是很直观。因此,我们可以使用一些技术来估计或模拟这一趋势,然后将其从序列中删除。有很多方法可以做到这一点,其中最常用的有:
- 聚合-取一段时间的平均值,如月/周平均值
- 平滑-取滚动平均值
- 多项式拟合-拟合回归模型
我将在这里讨论平滑,你应该尝试其他技术,以及可能解决其他问题。平滑是指采取滚动估计,即考虑过去的几个实例。有很多种方法,但我将在这里讨论其中的两种。
移动(滚动)平均
在这种方法中,我们根据时间序列的频率取“k”连续值的平均值。这里我们可以取过去一年的平均值,也就是最近12个值。pandas有确定滚动统计的特定功能。
pd.rolling_mean(ts_log,12) 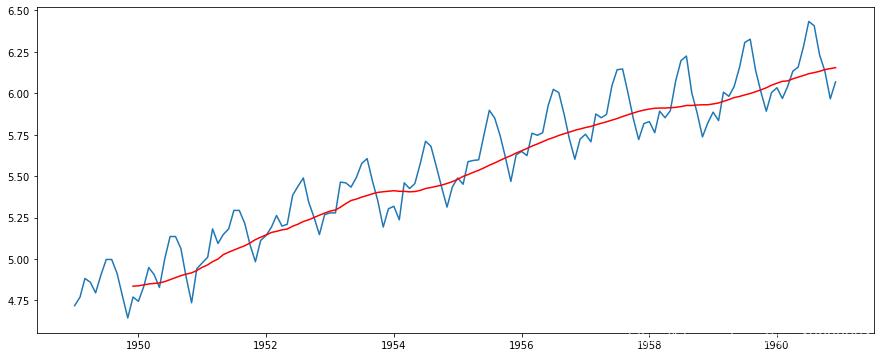
红线表示滚动平均值。我们从原来的数列中减去这个。注意,因为我们取最后12个值的平均值,所以滚动平均值没有定义前11个值。这可以观察到:
ts_log - moving_avg 
注意前11个是Nan。让我们删除这些NaN值并检查图以检验平稳性。
moving_avg_diff.dropna(inplace=True) 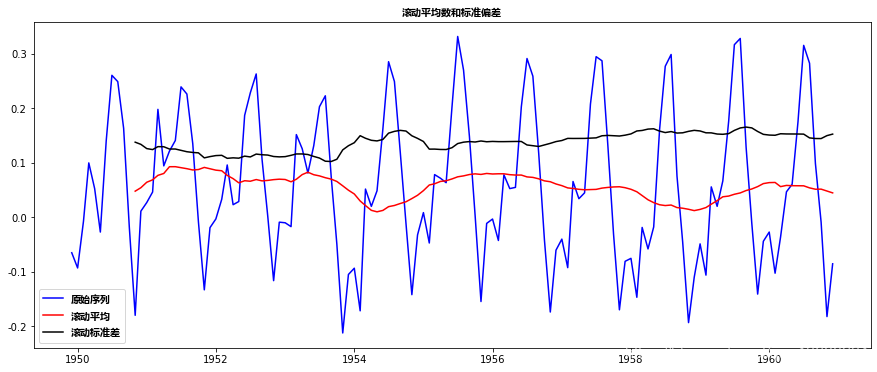
这看起来是一个更好的系列。滚动值似乎略有变化,但没有具体趋势。而且,检验统计量小于5%的临界值,所以我们可以用95%的置信度说这是一个平稳序列。
加权移动平均值(EWMA)
然而,这种方法的一个缺点是,时间段必须严格定义,在这种情况下,我们可以取年平均数,但在预测股票价格等复杂情况下,很难得出一个数字。所以我们取一个“加权移动平均值”,其中最近的值被赋予更高的权重。分配权重的方法有很多种,一种流行的方法是指数加权移动平均法,即用衰减因子将权重分配给所有先前的值。请在此处查找详细信息。这可以实现为:
ewma(ts_log, half=12) 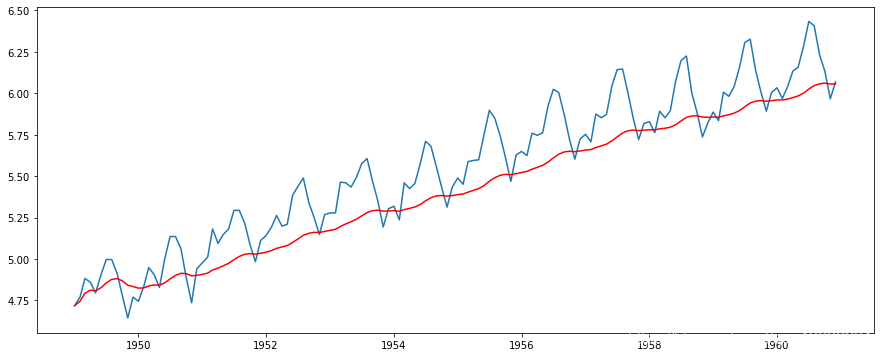
请注意,这里的参数“半衰期”用于定义指数衰减的量。这只是一个假设,很大程度上取决于业务领域。其他参数,如跨度和质心,也可以用来定义衰变,这将在上面共享的链接中讨论。现在,让我们从序列中删除此项并检查平稳性:
ts_log - expwighted_avg 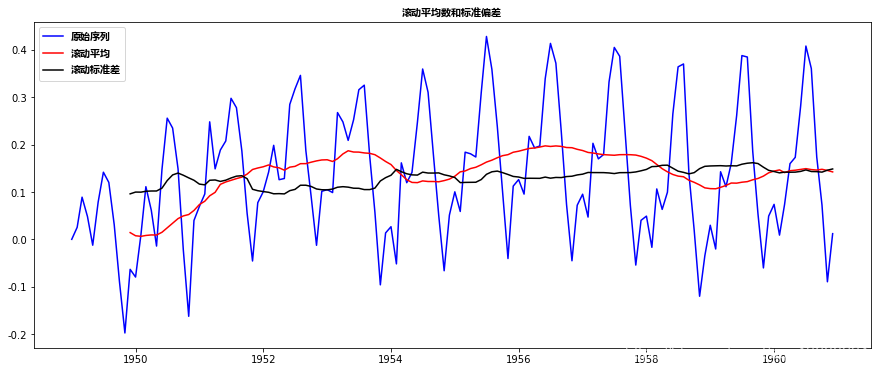
这个TS在平均值和标准偏差上的变化甚至更小。此外,检验统计量小于1%的临界值,这比前一种情况要好。注意,在这种情况下,不会出现缺失值,因为从开始算起的所有值都是给定的权重。所以即使没有以前的值,它也能工作。
消除趋势和季节性
以前讨论过的简单的趋势减少技术并不适用于所有情况,特别是那些具有高季节性的情况。让我们讨论两种消除趋势和季节性的方法:
- 差分-用特定的时间差取差分
- 分解–对趋势和季节性进行建模,并将其从模型中移除。
差分
处理趋势性和季节性最常用的方法之一是差分。在这项技术中,我们取某一时刻的观测值与前一时刻的观测值之差。这在改善平稳性方面效果很好。一阶差分可按如下方式进行:
ts_log - ts_log.shift() 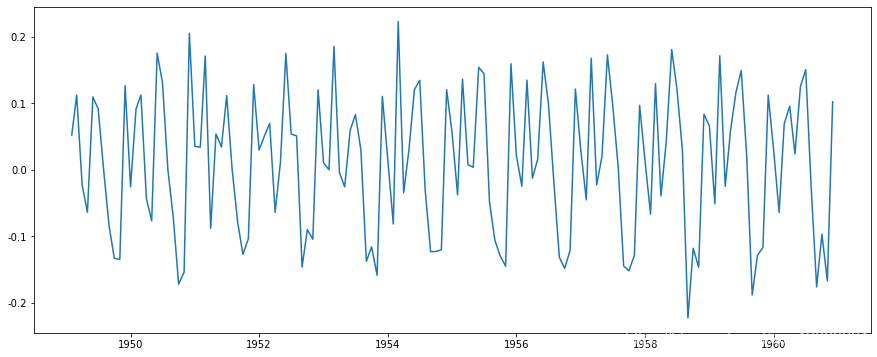
这似乎大大减少了这一趋势。让我们使用绘图进行验证:
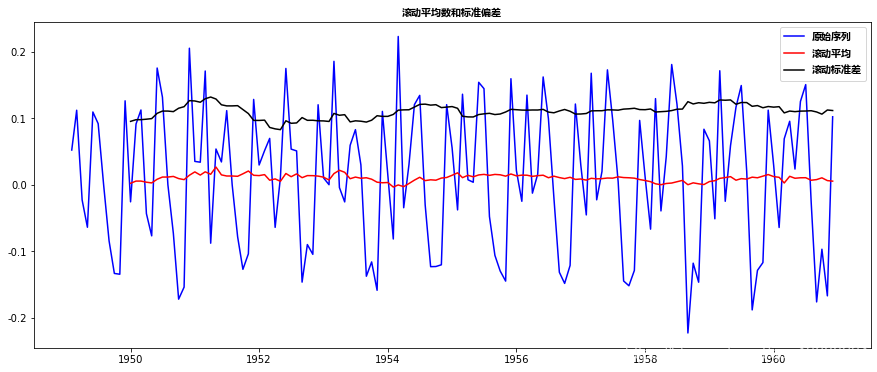
我们可以看到平均值和标准差随时间的变化很小。同时,Dickey-Fuller检验统计量小于10%的临界值,因此TS是平稳的,置信度为90%。我们也可以取二阶或三阶差,在某些应用中可能会得到更好的结果。
分解
在这种方法中,趋势和季节性都被分别建模,序列的其余部分被返回。我将跳过统计数据得出结果:
decompose(ts_log)
decomposition.trend
decomposition.seasonal
decomposition.resid 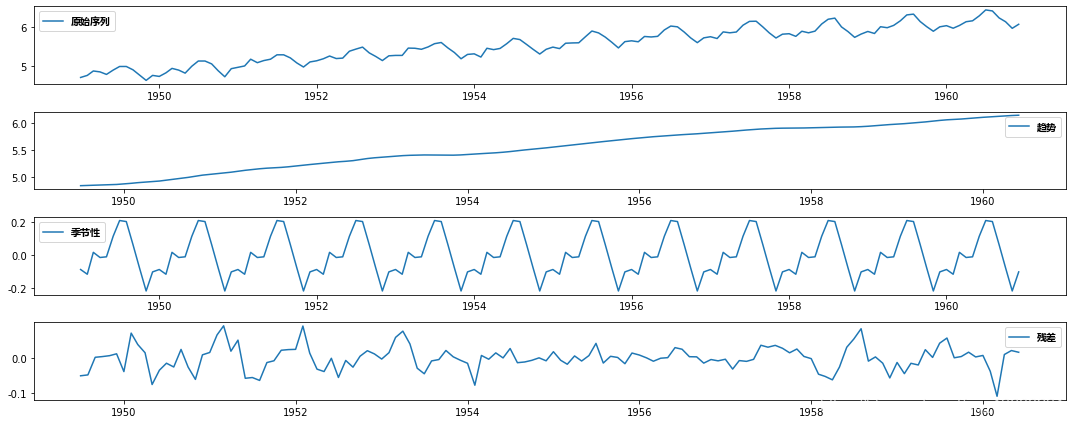
在这里我们可以看到趋势,季节性是从数据中分离出来的,我们可以对残差进行建模。让我们检查残差的平稳性:
ts_log_decompose = residual 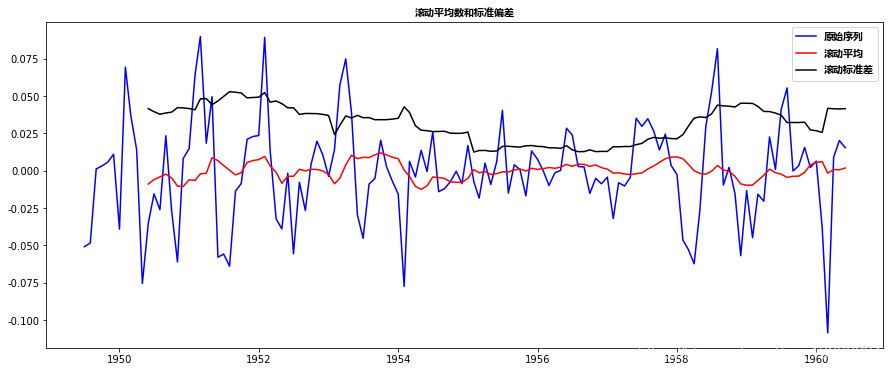
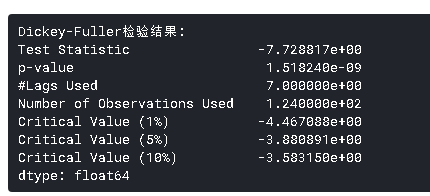
Dickey-Fuller检验统计量显著低于1%的临界值。所以这个t非常接近平稳。另外,您应该注意到,在本例中,将残差转换为未来数据的原始值不是很直观。
5预测时间序列
我们看到了不同的技术,所有这些技术都相当好地使TS平稳。因为这是一种非常流行的技术,所以让我们在差分后在TS上建立模型。此外,在这种情况下,将噪声和季节性添加回预测残差中相对容易。执行趋势和季节性估计技术后,可能有两种情况:
- 一个严格平稳的序列,值之间没有依赖关系。这是一个简单的例子,我们可以将残差建模为白噪声。但这是非常罕见的。
- 值之间有显著相关性的一系列。在这种情况下,我们需要使用一些统计模型,如ARIMA来预测数据。
让我简单介绍一下ARIMA。我不会深入讨论技术细节,但如果您希望更有效地应用它们,您应该详细了解这些概念。ARIMA代表自回归综合移动平均线。平稳时间序列的ARIMA预测只不过是一个线性(类似于线性回归)方程。预测因子取决于ARIMA模型的参数(p,d,q):
- AR(自回归)项数(p): AR项是因变量的滞后。例如,如果p为5,x(t)的预测因子为x(t-1)….x(t-5)。
- 移动平均线项数(q):移动平均线项是预测方程中的滞后预测误差。例如,如果q是5,x(t)的预测因子将是e(t-1)….e(t-5),其中e(i)是移动平均在第一个瞬间和实际值之间的差值。
- 差分的数量(d):这些是非季节性差分的数量,即在这种情况下,我们取一阶差分。所以我们可以传递这个变量,让d=0或者传递原始变量,让d=1。两者都会产生相同的结果。
这里的一个重要问题是如何确定“p”和“q”的值。我们先来讨论一下。
- 自相关函数(ACF):它是TS与自身滞后之间相关性的度量。例如,在滞后5时,ACF会将“t1”…“t2”时刻的序列与“t1-5”…“t2-5”时刻的序列进行比较(t1-5和t2是终点)。
- 偏自相关函数(PACF):它测量了TS之间的相关性, 但在消除了已经解释的变化之后。例如,在滞后5,它将检查相关性,但消除已经由滞后1到4解释的影响。
差分后TS的ACF和PACF图可以绘制为:
#绘图ACF:
plt.subplot(121)
plt.plot(lag_acf)
plt.axhline(y=0,linestyle='--',color='gray')
#绘图PACF:
plt.subplot(122)
plt.plot(lag_pacf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.tight_layout()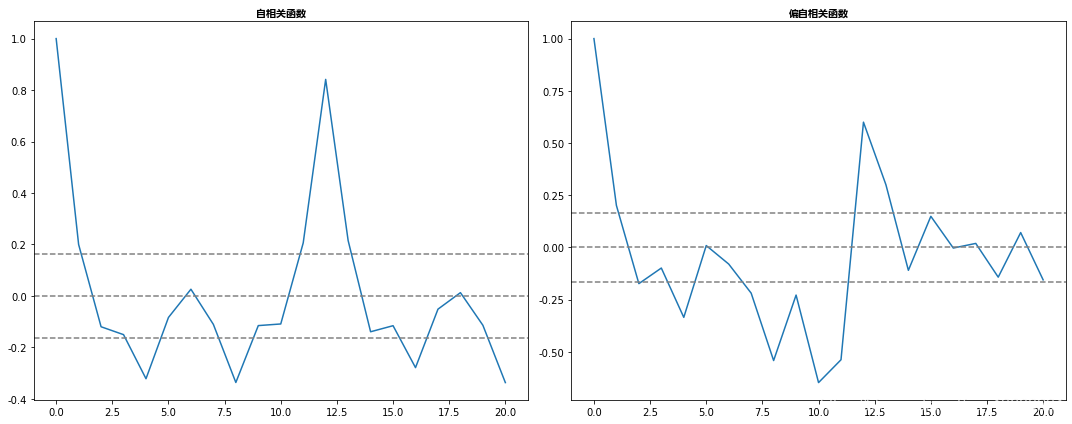
在这个图中,0两边的两条虚线是置信区间。这些可用于确定“p”和“q”值,如下所示:
- p–PACF图表第一次穿过置信区间上限的滞后值。如果你仔细观察,在这种情况下,p=2。
- q–ACF图表首次穿过置信区间上限的滞后值。如果你仔细观察,在这种情况下,q=2。
现在,让我们建立3种不同的ARIMA模型,既考虑个体效应,也考虑组合效应。我也会输出RSS。请注意,这里的RSS是残差值,而不是实际序列。
我们需要先加载ARIMA模型:
可以使用ARIMA的order参数指定p、d、q值,该参数采用元组(p、d、q)。让我们模拟3个案例:
AR模型
model.fit(disp=-1)
plt.plot(ts_log_diff) 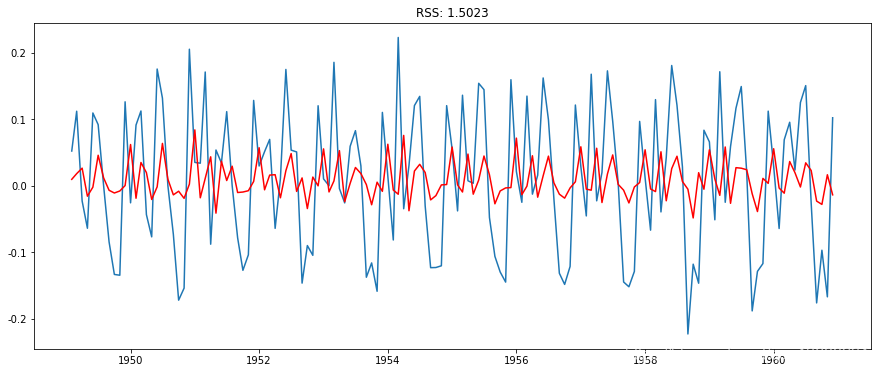
MA模型
results_MA = model.fit(disp=-1)
plt.plot(ts_log_diff) 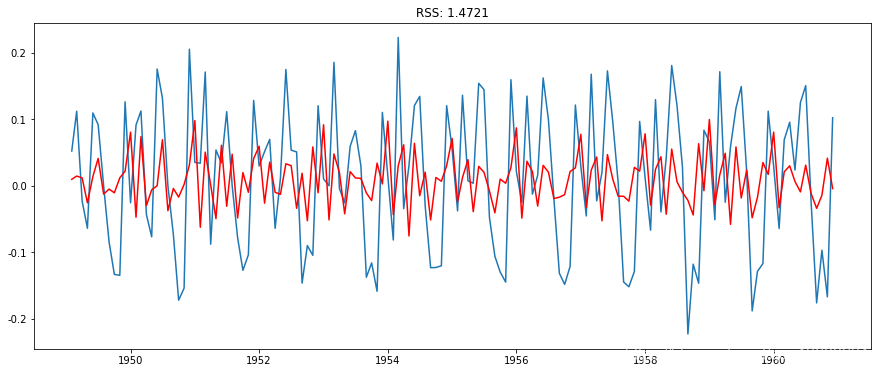
在这里,我们可以看到AR和MA模型有几乎相同的RSS,但是结合起来会更好。现在,我们剩下最后一步,即将这些值恢复到原始比例。
组合模型
plt.plot(ts_log_diff)
plt.plot(results_ARIMA.fittedvalues, color='red') 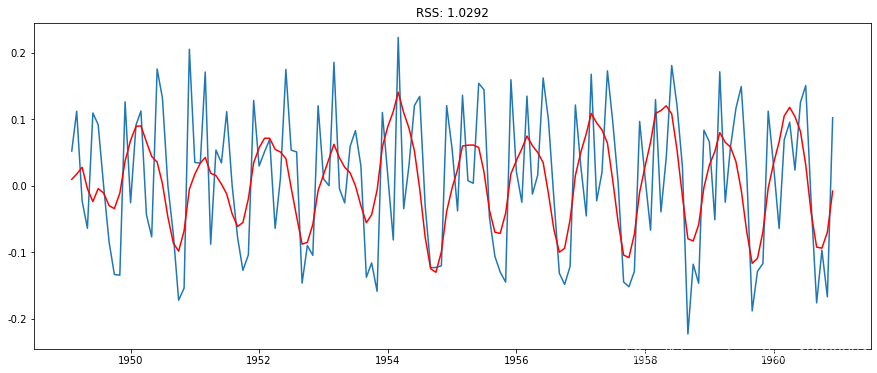
回到原来的比例
由于组合模型给出了最佳结果,让我们将其缩放回原始值,看看它的预测表现如何。第一步是将预测结果存储为一个单独的序列并观察它。
请注意,这些开始于’1949-02-01’,而不是第一个月。为什么?这是因为我们取了一个滞后1,第一个元素之前没有任何东西可以减去。将差分转换为对数刻度的方法是将这些差分连续地添加到基数上。一个简单的方法是首先确定索引处的累积和,然后将其添加到基数中。累积总和如下所示:
您可以使用前面的输出快速地做一些计算,以检查这些是否正确。接下来我们要把它们加到底数上。为此,让我们创建一个以所有值作为基数的序列,并将其差分相加。这可以这样做:
这里的第一个元素是基数本身,然后从那里累计加值。最后一步是取指数并与原数列进行比较。
plt.plot(predictions_ARIMA) 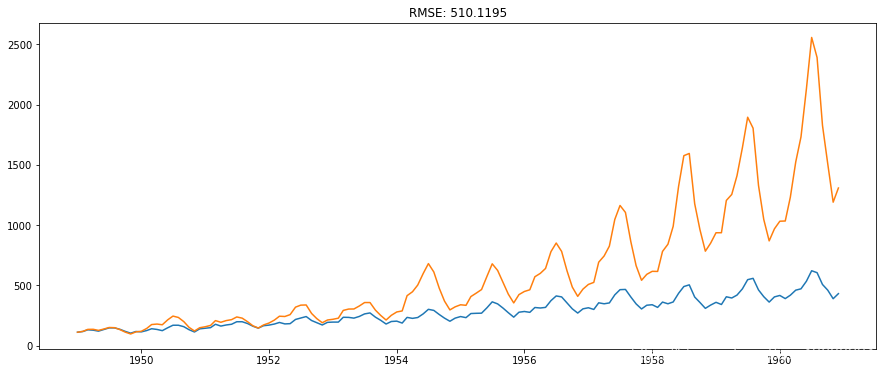
这些都是Python中的内容。我们来学习一下如何在R中实现时间序列预测。
R时间序列预测
第一步:读取数据,计算基本总结
#安装包并调用库
install.packages("tseries")
#读取Airpaseengers数据
tsdata<-AirPassengers
#识别数据类别
class(tsdata)
#观察时间序列数据
tsdata
#数据摘要
dfSummary(tsdata)输出
class(tsdata)
"ts"
> #观察时间序列数据
> tsdata
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 112 118 132 129 121 135 148 148 136 119 104 118
1950 115 126 141 135 125 149 170 170 158 133 114 140
1951 145 150 178 163 172 178 199 199 184 162 146 166
1952 171 180 193 181 183 218 230 242 209 191 172 194
1953 196 196 236 235 229 243 264 272 237 211 180 201
1954 204 188 235 227 234 264 302 293 259 229 203 229
1955 242 233 267 269 270 315 364 347 312 274 237 278
1956 284 277 317 313 318 374 413 405 355 306 271 306
1957 315 301 356 348 355 422 465 467 404 347 305 336
1958 340 318 362 348 363 435 491 505 404 359 310 337
1959 360 342 406 396 420 472 548 559 463 407 362 405
1960 417 391 419 461 472 535 622 606 508 461 390 432
> #
tsdata
Dimensions: 144 x 1
Duplicates: 26
----------------------------------------------------------------------------------------------------
No Variable Stats / Values Freqs (% of Valid) Graph Valid Missing
---- ---------- -------------------------- ----------------------- --------------------- -------- --
1 tsdata Mean (sd) : 280.3 (120) 118 distinct values . : . 144 0
[ts] min < med < max: Start: 1949-01 : : . . : (100%) (0%)
104 < 265.5 < 622 End : 1960-12 : : : : :
IQR (CV) : 180.5 (0.4) : : : : : : :
: : : : : : : : . .
----------------------------------------------------------------------------------------------------第2步:检查时间序列数据的周期并绘制原始数据
#检查数据并绘制原始数据
plot(tsdata, ylab="乘客(1000人)", type="o")输出
cycle(tsdata)
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 1 2 3 4 5 6 7 8 9 10 11 12
1950 1 2 3 4 5 6 7 8 9 10 11 12
1951 1 2 3 4 5 6 7 8 9 10 11 12
1952 1 2 3 4 5 6 7 8 9 10 11 12
1953 1 2 3 4 5 6 7 8 9 10 11 12
1954 1 2 3 4 5 6 7 8 9 10 11 12
1955 1 2 3 4 5 6 7 8 9 10 11 12
1956 1 2 3 4 5 6 7 8 9 10 11 12
1957 1 2 3 4 5 6 7 8 9 10 11 12
1958 1 2 3 4 5 6 7 8 9 10 11 12
1959 1 2 3 4 5 6 7 8 9 10 11 12
1960 1 2 3 4 5 6 7 8 9 10 11 12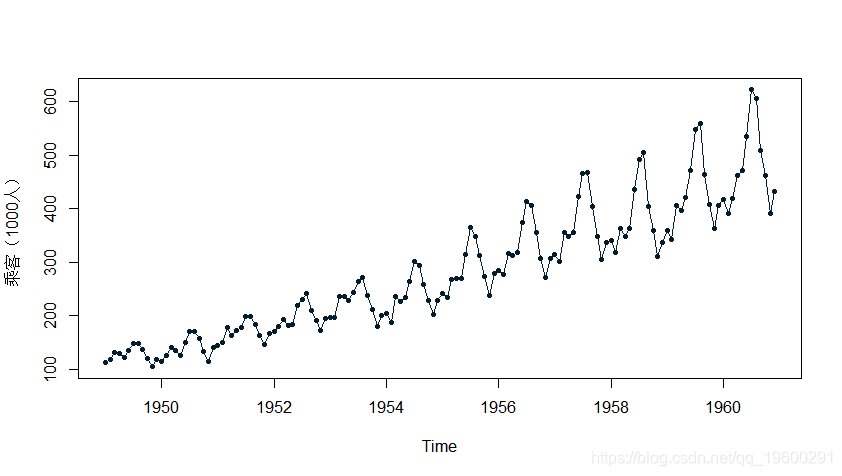
步骤3:分解时间序列数据
#将数据分解为趋势、季节性和随机误差分量
plot(tsdata_decom)输出
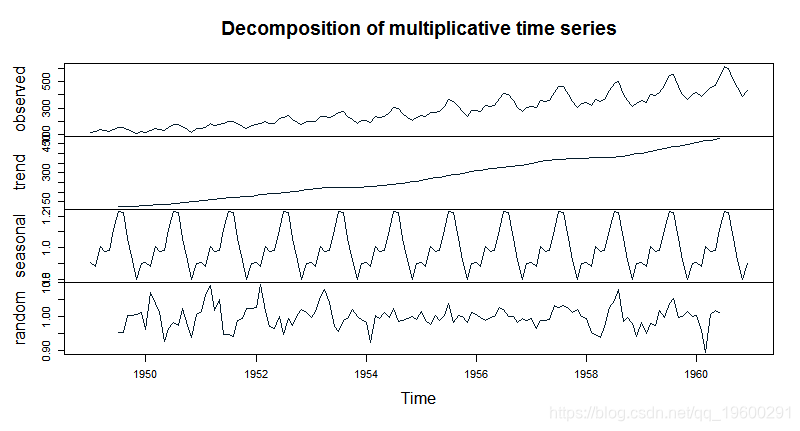
第四步:检验数据的平稳性
#测试数据的平稳性
#单位根检验
adf(tsdata)
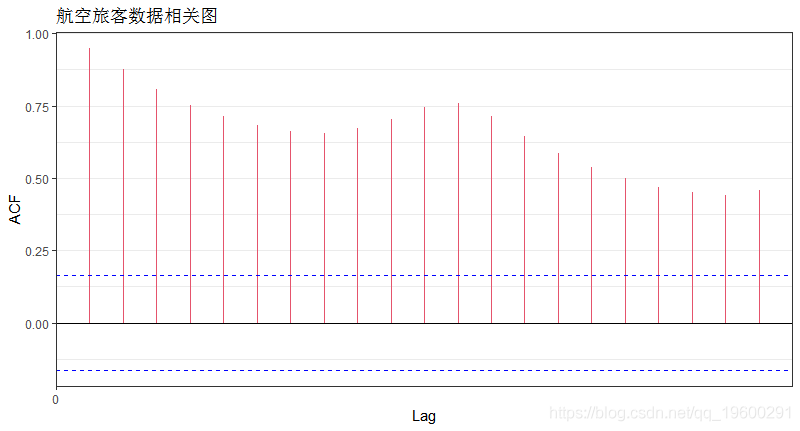
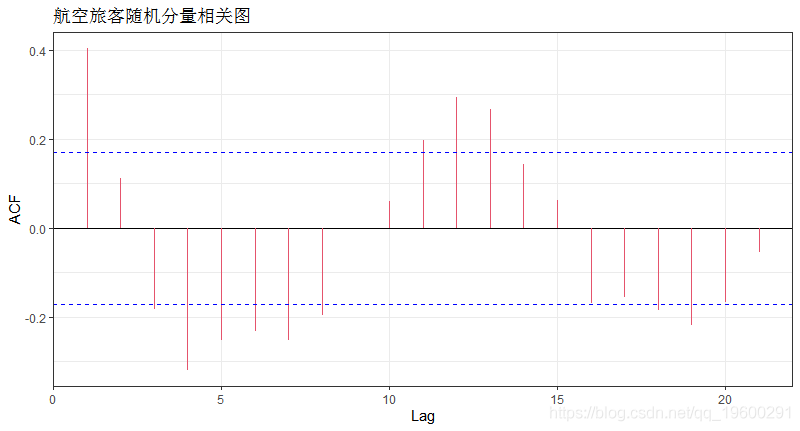
#自相关检验
plot(acf(tsdata,plot=FALSE))+ labs(title="航空旅客数据相关图")
plot(acf(tsdata_decom$random,plot=FALSE)) 输出
Augmented Dickey-Fuller Test
data: tsdata
Dickey-Fuller = -7.3186, Lag order = 5, p-value = 0.01
alternative hypothesis: stationary the p-value is 0.01 which ip值为0.01,小于0.05,因此,我们拒绝了零假设,因此时间序列是平稳的。s <0.05, therefore, we reject the null hypothesis and hence time series is stationary.
步骤5:拟合模型
最大滞后为1个月或12个月,表明与12个月周期正相关。
自动绘制7:138的随机时间序列观测值,不包括NA值
#拟合模型
#线性模型
plot(tsdata) + smooth(method="lm")
#ARIMA 模型
arimats 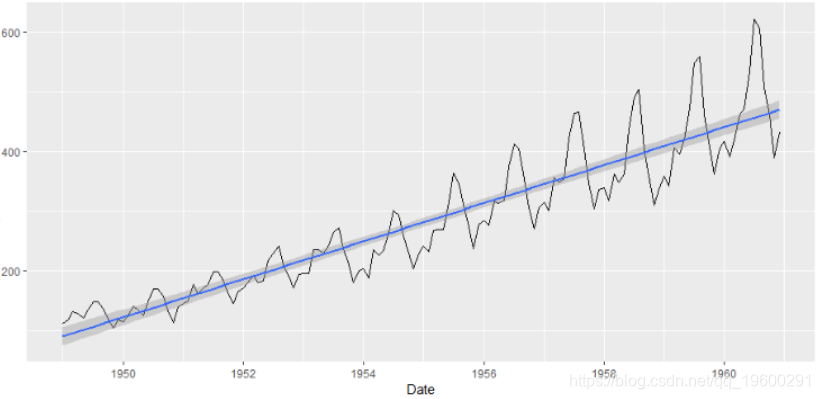
Series: tsdata
ARIMA(2,1,1)(0,1,0)[12]
Coefficients:
ar1 ar2 ma1
0.5960 0.2143 -0.9819
s.e. 0.0888 0.0880 0.0292
sigma^2 estimated as 132.3: log likelihood=-504.92
AIC=1017.85 AICc=1018.17 BIC=1029.35 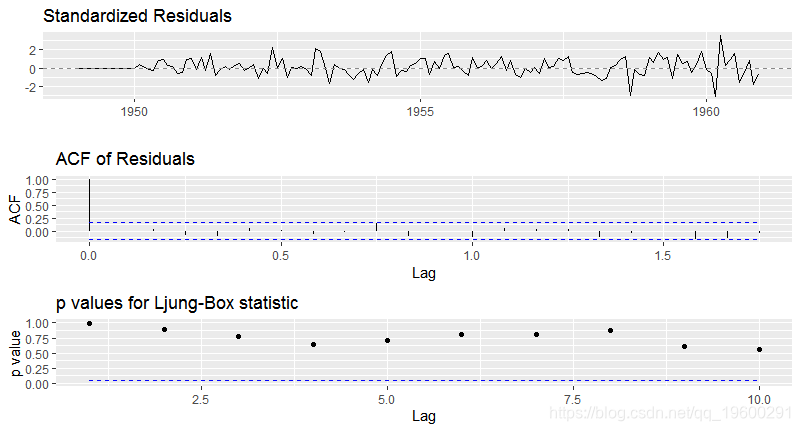
第6步:预测
#Arima模型的预测
fore(arimats, level = c(95)) 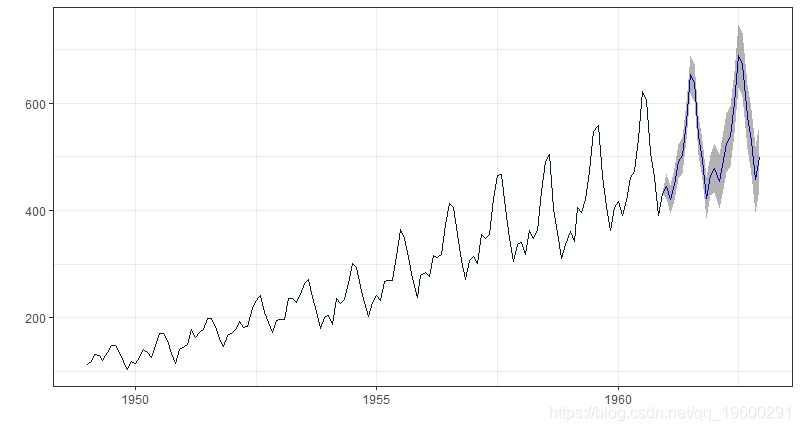
最后我们有一个原始数据的预测。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究
Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证 视频讲解|Python图神经网络GNN原理与应用探索交通数据预测
视频讲解|Python图神经网络GNN原理与应用探索交通数据预测 专题|LSTM-XGBoost,ARMA-LSTM,LDA-LSTM黄金比特币价格混合预测,蔬菜包发放时空协同调配,知乎综艺评论情感时序洞察
专题|LSTM-XGBoost,ARMA-LSTM,LDA-LSTM黄金比特币价格混合预测,蔬菜包发放时空协同调配,知乎综艺评论情感时序洞察
