隐马尔可夫模型(HMM)简介
隐马尔可夫模型(HMM)是一个在你观察到的输出顺序,但不知道状态序列模型产生输出的过程。
隐马尔可夫模型的分析试图从观察到的数据中恢复状态序列。
可下载资源
例如,考虑具有两个状态和六个可能输出的马尔可夫模型。该模型使用:
- 红色骰子,有六个面,标记为1到6。
- 一个绿色骰子,具有十二个侧面,其中五个侧面标记为2到6,其余七个侧面标记为1。
- 加权的红色硬币,正面出现概率为.9,背面出现概率为1.。
- 加权绿色硬币,其正面概率为0.95,背面概率为.05。
该模型使用以下规则从集合{1、2、3、4、5、6}中创建数字序列:
- 首先滚动红色骰子,然后写下出现的数字 。
- 投掷红色硬币并执行以下操作之一:
- 如果结果为正面,则滚动红色骰子并记下结果。
- 如果结果是反面,则滚动绿色骰子并记下结果。
- 在随后的每个步骤中,您翻转与上一步中滚动的骰子颜色相同的颜色的硬币。如果硬币正面朝上,则与上一步骤滚动相同的骰子。如果硬币出现反面,请切换到另一个骰子。
该模型的状态图具有红色和绿色两种状态,如下图所示。
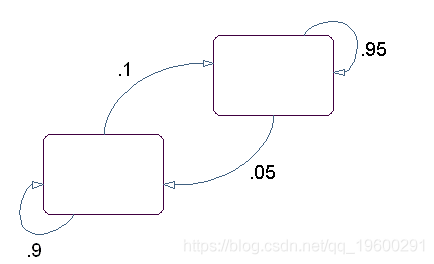

您可以通过滚动具有与状态相同颜色的骰子来确定状态的发射。您可以通过翻转与状态相同颜色的硬币来确定到下一个状态的过渡。
转换矩阵为:
T = [0.90.050.10.95]
输出矩阵为:
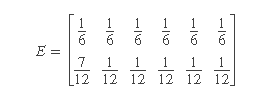

该模型不是隐藏的,因为您可以从硬币和骰子的颜色知道状态的顺序。但是,假设其他人 没有向您显示骰子或硬币。您所看到的只是输出的顺序。如果开始看到的数字比其他数字多1,则可能会怀疑骰子处于绿色状态,但由于无法看到要滚动的骰子的颜色,因此无法确定。
隐藏的马尔可夫模型提出以下问题:
- 给定一系列输出,最可能的状态路径是什么?
- 给定一系列输出,您如何估算模型的转换和输出概率?
- 什么是后验概率?
分析隐马尔可夫模型
本节说明如何来分析隐马尔可夫模型。
生成测试序列
TRANS = [.9 .1; .05 .95];
EMIS = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6;...
7/12, 1/12, 1/12, 1/12, 1/12, 1/12];
要从模型生成状态和发射的随机序列 :
输出seq是序列,输出states是状态序列。
估计状态序列
likelystates是与长度相同的序列seq。
要测试的准确性hmmviterbi 。
sum(states==likelystates)/1000
ans =
0.8200
在这种情况下,最有可能的状态序列在82%的时间内与随机序列一致。
估算转移和输出矩阵
返回转换矩阵和输出矩阵的估计值:
您可以将输出与原始 矩阵进行比较, TRANS并且EMIS:
TRANS
TRANS =
0.9000 0.1000
0.0500 0.9500
EMIS
EMIS =
0.1667 0.1667 0.1667 0.1667 0.1667 0.1667
0.5833 0.0833 0.0833 0.0833 0.0833 0.0833
假设您对TRANS和 有以下初步猜测EMIS。
TRANS_GUESS = [.85 .15; .1 .9];
EMIS_GUESS = [.17 .16 .17 .16 .17 .17;.6 .08 .08 .08 .08 08];
您估计TRANS并EMIS如下:
TRANS_EST2 =
0.2286 0.7714
0.0032 0.9968
EMIS_EST2 =
0.1436 0.2348 0.1837 0.1963 0.2350 0.0066
0.4355 0.1089 0.1144 0.1082 0.1109 0.1220
如果算法在最大迭代次数(默认值为)内未能达到此容差100,则算法将暂停。
如果算法未能达到所需的容差,请使用以下命令增加最大迭代次数的默认值:
其中,maxiter是算法执行的最大步骤数。
估计后验状态概率
输出PSTATES为M × L矩阵,其中M为状态数,L为的长度seq。PSTATES(i,j)是条件概率,该模型处于状态i时,它产生j的 seq给出的是,seq 。
要返回序列概率的对数seq,请使用第二个输出参数hmmdecode:
随着序列长度的增加,序列的概率趋于0 。
更改初始状态分布
默认情况下, 隐藏的Markov模型函数从状态1开始。换句话说,初始状态的分布将其所有概率质量都集中在状态1处。要分配不同的概率分布,p = [ p 1,p 2,…,p M ],到M个初始状态,执行以下操作:
如果转换矩阵和发射矩阵分别为TRANS和EMIS,则可以使用以下命令来创建增强矩阵:
TRANS_HAT = [0 p; zeros(size(TRANS,1),1) TRANS];
EMIS_HAT = [zeros(1,size(EMIS,2)); EMIS];可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究
MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究 R语言股价跳跃点识别:隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析
R语言股价跳跃点识别:隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析 MATLAB模糊C均值聚类FCM改进的推荐系统协同过滤算法分析MovieLens电影数据集
MATLAB模糊C均值聚类FCM改进的推荐系统协同过滤算法分析MovieLens电影数据集 Python、MATLAB股票投资:ARIMA模型最优的选股方案和投资组合方案与预测
Python、MATLAB股票投资:ARIMA模型最优的选股方案和投资组合方案与预测


