本教程使用R 中的包介绍了具有非信息先验的贝叶斯 GLM(广义线性模型)。
本文特别关注贝叶斯逻辑回归在二元结果和计数/比例结果场景中的使用,以及模型评估的相应方法。使用教育数据示例。 此外, 本文简要演示了贝叶斯 GLM 模型的多层次扩展。
贝叶斯逻辑回归是一种统计方法,它结合了贝叶斯理论和逻辑回归模型。在贝叶斯逻辑回归中,通过引入先验分布来对模型参数进行估计,从而得到后验分布。
这种方法可以处理不确定性,并且能够在小样本情况下进行有效的推断。
它在二元结果(例如分类问题中的两个类别)和计数/比例结果场景中有广泛应用,同时也有相应的模型评估方法来判断模型的性能和准确性。
本教程遵循以下结构:
1. 准备工作;
2.GLM介绍;
3. 教育数据;
4. 数据准备;
5.贝叶斯逻辑回归;
6.贝叶斯二项Logistic回归;
7.贝叶斯层次逻辑回归。
准备
本教程需要:
– 假设检验和统计推断的基础知识;
– 贝叶斯统计推断的基础知识;
– R 编码的基础知识;
– 使用 tidyverse 进行绘图和数据操作的基本知识。
GLM 一般是指 generalized linear model ,也就是广义线性模型;而非 general linear model,也就是一般线性模型;而GLMM (generalized linear mixed model)是广义线性混合模型。
广义线性模型GLM很简单,举个例子,药物的疗效和服用药物的剂量有关。这个相关性可能是多种多样的,可能是简单线性关系(发烧时吃一片药退烧0.1度,两片药退烧0.2度,以此类推;这种情况就是一般线性模型),也可能是比较复杂的其他关系,如指数关系(一片药退烧0.1度,两片药退烧0.4度),对数关系等等。这些复杂的关系一般都可以通过一系列数学变换变成线性关系,以此统称为广义线性模型。
广义线性混合模型GLMM比较复杂,GLM要求观测值误差是随机的,而GLMM则要求误差值并非随机,而是呈一定分布的。举个例子,我们认为疗效可能与服药时间相关,但是这个相关并不是简简单单的疗效随着服药时间的变化而改变。更可能的是疗效的随机波动的程度与服药时间有关。比如说,在早上10:00的时候,所有人基本上都处于半饱状态,此时吃药,相同剂量药物效果都差不多。但在中午的时候,有的人还没吃饭, 有的人吃过饭了,有的人喝了酒,结果酒精和药物起了反应,有的人喝了醋,醋又和药物起了另一种反应。显然,中午吃药会导致药物疗效的随机误差非常大。这种疗效的随机误差(而非疗效本身)随着时间的变化而变化,并呈一定分布的情况,必须用广义线性混合模型了。
广义线性模型 (GLM) 介绍
广义线性模型,是为了克服线性回归模型的缺点出现的,是线性回归模型的推广。首先自变量可以是离散的,也可以是连续的。离散的可以是0-1变量,也可以是多种取值的变量。广义线性模型取消了对残差(因变量)服从正态分布的要求。残差不一定要服从正态分布,可以服从二项、泊松、负二项、正态、伽马、逆高斯等分布,这些分布被统称为指数分布族。
教育数据
本教程中使用的数据是教育数据。
这些数据来自于全国性的小学教育调查。数据中的每一行都是指一个学生。结果变量REPEAT是一个二分变量,表示一个学生在小学教育期间是否留过级。SCHOOLID变量表示一个学生所在的学校。个人层面的预测因素包括。性别(0=女性,1=男性)和PPED(受过学前教育,0=没有,1=有)。学校层面的是MSESC,代表学校平均SES(社会经济地位)得分。
视频
R语言中RStan贝叶斯层次模型分析示例
视频
逻辑回归Logistic模型原理和R语言分类预测冠心病风险实例
本教程试图使用教育数据回答的主要研究问题是:
- 忽略数据的层次结构,性别和学前教育对学生是否留级有什么影响?
- 忽略数据的层次结构,学校平均SES对学生留级比例的影响是什么?
- 考虑到数据的层次结构,性别、学前教育和学校平均社会经济地位对学生是否留级有什么影响?
这三个问题分别通过使用以下模型来回答: 贝叶斯二元逻辑回归;贝叶斯二项式逻辑回归;贝叶斯多层次二元逻辑回归。
数据准备
加载必要的包
library(tidyverse) #用于数据处理和绘图 library(sjstats) #用于计算类内相关(ICC)。 library(ROCR) #用于计算曲线下面积(AUC)的统计数据 library(modelr) #用于数据处理
导入数据

数据处理
Ed\_e <- Ed\_Ra %>%
mtae(SCHLI = fcor(SCLID,
SEX = if_se(SX == 0, "grl", "by"),
SEX = facor(SEX, lvls = c("gil", "boy")),
PED = if_ese(PPED == 0, "no", "yes"),
PED = facr(PPD, leel = c("no", "yes")))

检查缺失数据
New %>% summar(lst(~sm(is.na(.)))) %>% gaer()

该数据缺少 1066 个MSESC 变量的观测 值。缺失数据的处理本身就是一个复杂的话题。为方便起见,我们在本教程中简单地按列删除缺少数据的案例。
New <- New %>% fltr(!is.na(MEC))
贝叶斯二元逻辑回归(具有非信息先验)
探索数据: REPEAT 与 SEX 和 PPED
gru_y(SEX) %>% suma(RPEAT = sm(REEAT))

group_by(PED) %>% sumais(RPEAT = sum(REEA))

看来,留级的学生人数在男女之间有很大的不同,更多的男学生不得不留级。更多没有接受过学前教育的学生留级。这一观察结果表明,性别和学前教育可能对留级有预测作用。
拟合贝叶斯二元 Logistic 回归模型
执行贝叶斯 GLM。但是,请注意,在 family 参数中,我们需要为二元逻辑回归指定 bernoulli (而不是 binomial)。还有一些额外的参数: warmup 指定预烧期(即应该丢弃的迭代次数); iter 指定总迭代次数; chains 指定链数; inits 指定迭代的起始值(通常你可以使用参数的最大似然估计作为起始值,或者简单地要求算法从零开始); cores 指定用于算法的核心数; seed 指定随机种子,允许复制结果。
请参阅下面的具有两个预测变量的二元逻辑回归模型的规范,不使用信息先验。
Baysoel(fr= RPEAT ~ SX + PED, famly = benouli(link = "logit"), )


想了解更多关于模型定制、咨询辅导的信息?
模型收敛
在查看模型摘要之前,我们应该检查是否存在两条链不收敛的依据。
随时关注您喜欢的主题
首先,我们为每个感兴趣的参数绘制毛毛虫图。
plot(BysMenr, tpe = "trce")

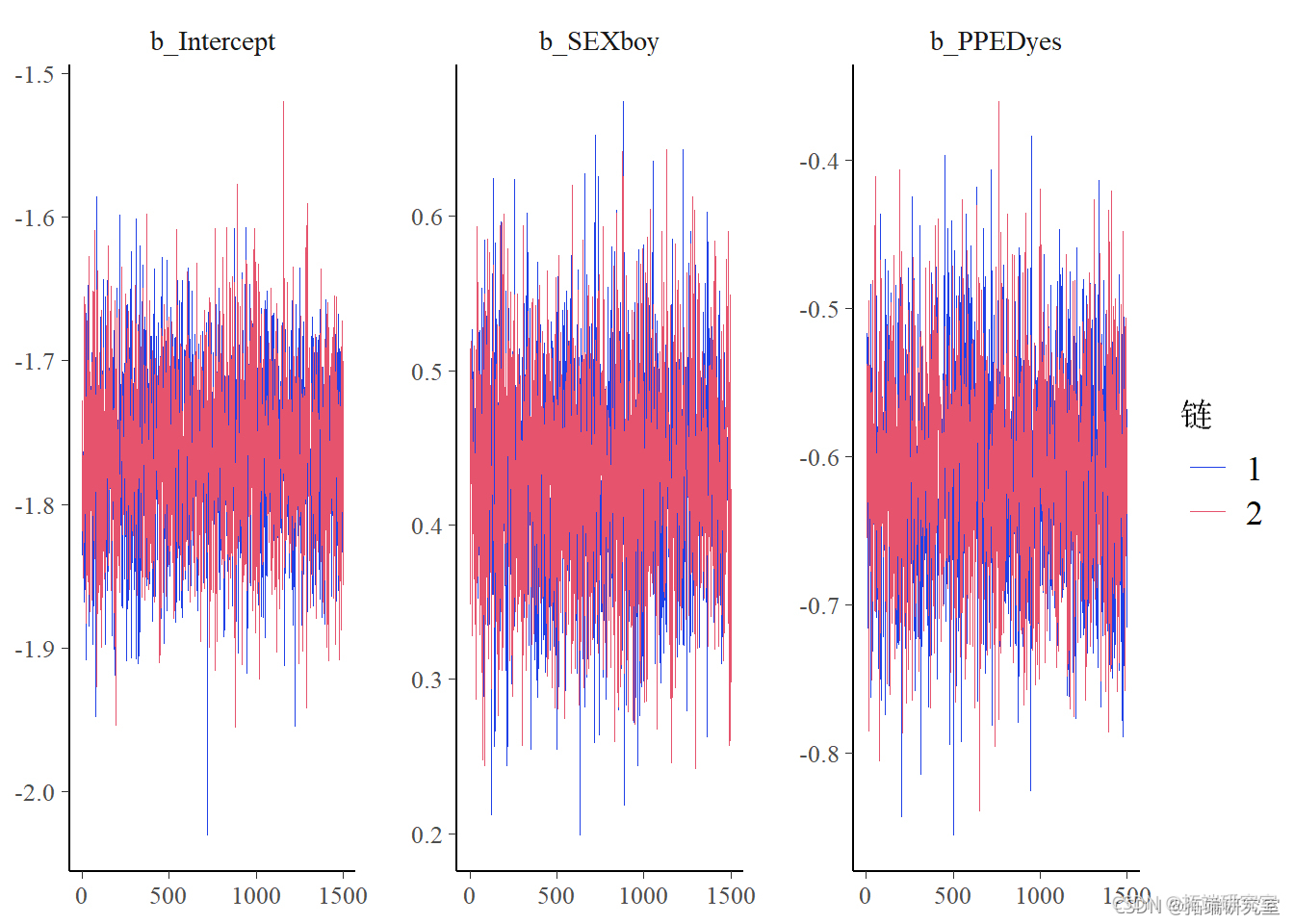
该图仅显示预烧期后的迭代。两条链对所有参数都很好地混合,因此,我们得出收敛的依据。
我们还可以检查自相关,考虑到强自相关的存在会使方差估计产生偏差。
plot(Byory , tye = "afbar")
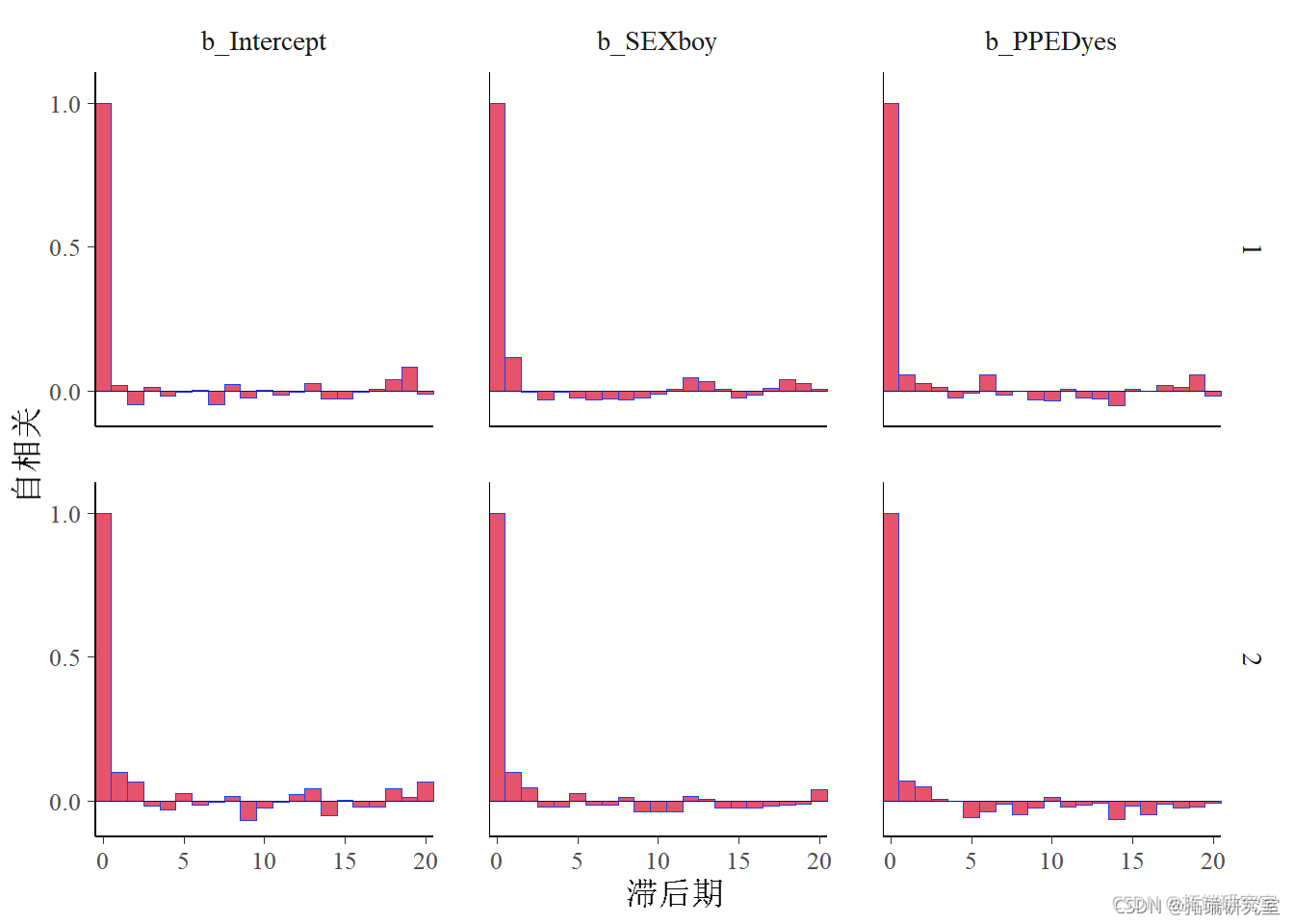
该图没有显示两个链中所有模型变量的自相关证据,因为自相关参数都迅速减小到零附近。
解释
现在,我们可以进行模型的解释。下面是贝叶斯二元逻辑回归模型的模型摘要。
smma(Bayoenry)
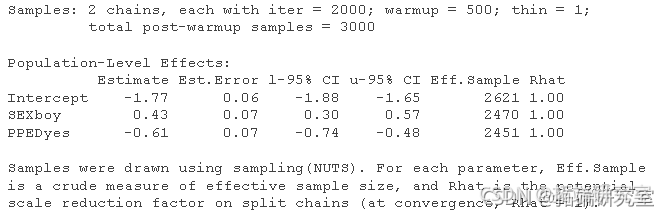
为了比较,下面是频率论二元逻辑回归模型的模型摘要。
从上面的模型总结中,我们可以看到贝叶斯模型的估计与频率论模型的估计几乎相同。
glm(fma= REEA ~ SX + PPD, famly = bnmia(link = "logit"), daa = Ne)

这些估计的解释在频率论和贝叶斯模型中是相同的。然而,请注意,不确定性区间的解释在两个模型之间是不同的。在频率论模型中,使用 95% 的不确定性区间(置信区间)背后的想法是,在重复抽样的情况下,95% 的结果不确定性区间将覆盖真实的总体值。这让我们可以说,对于给定的 95% 置信区间,我们有 95% 的置信区间包含真实的总体值。然而,它不允许我们说置信区间有 95% 的机会包含真实的总体值(即 频率论不确定性区间不是概率陈述)。相比之下,在贝叶斯模型中,95% 的不确定性区间(称为可信区间)更具可解释性,表明真实总体值有 95% 的机会落入该区间内。当 95% 可信区间不包含零时,我们得出结论,相应的模型参数可能有意义。
让我们使用可视化点估计及其相关的不确定性区间 。
plot(asMdeBinr, tye = "aeas", prb = 0.95)
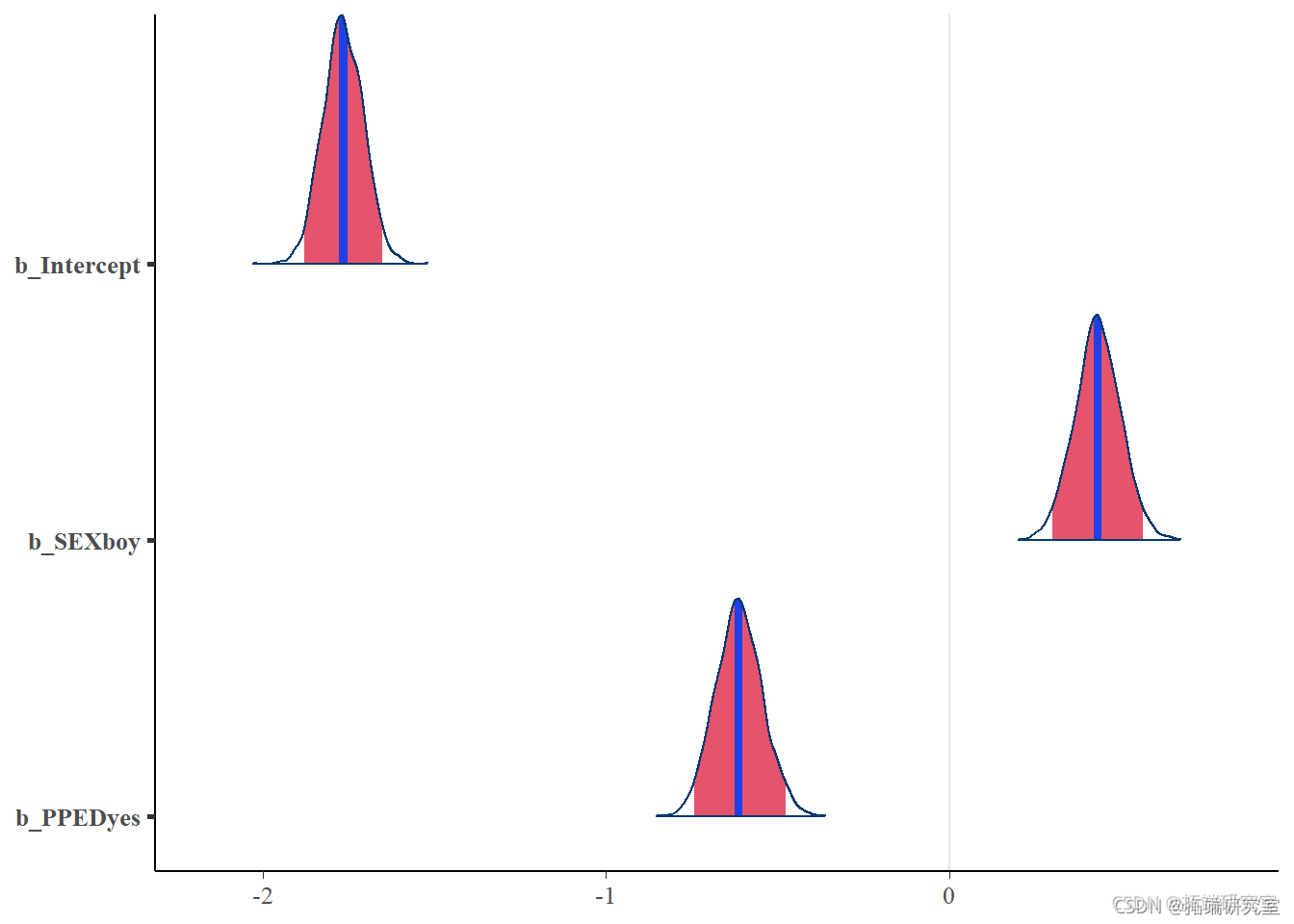
上图显示了参数估计的密度。每个密度中的深蓝色线表示点估计,而浅蓝色区域表示 95% 的可信区间。我们可以很容易地看到, SEX 和 PPED 都是有意义的预测变量,因为它们的置信区间不包含零,并且它们的密度具有非常窄的形状。 SEX 正面预测学生留级的概率,而PPED 负面预测 。具体来说,与作为女孩相比,作为男孩更有可能留级,假设其他一切都保持不变。假设其他一切都保持不变,之前的教育不太可能导致留级。
为了解释参数估计的值,我们需要对估计取幂。见下文。
ex(fef(BeBiry)\[,-2\])

我们还可以绘制这些参数估计的密度。
plt(ay\_dl\_iay, type ="areas", prb = 0.95, trnsoatos = "exp") + mne(xtp = 1, clo = gey")
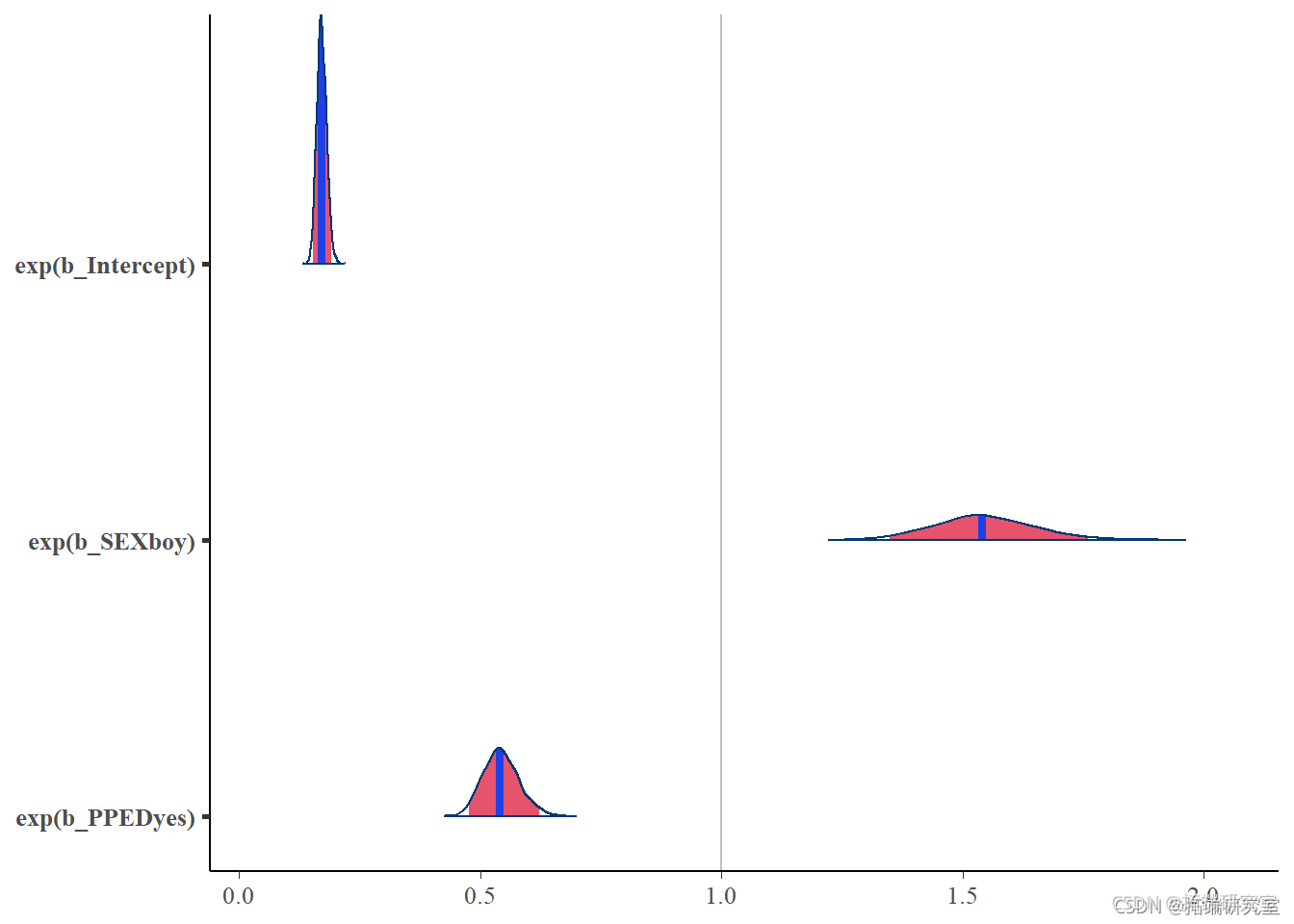
请注意,参数估计的解释与几率而不是概率有关。几率的定义是。P(事件发生)/P(事件未发生)。在本分析中,假设其他一切保持不变,与女孩相比,男孩会增加54%的留级几率;与没有学前教育相比,假设其他一切保持不变,拥有学前教育会降低(1-0.54)%=46%的留级几率。留级的基线几率(由截距项表示),即如果你是一个没有受过学校教育的女孩,大约是17%。
参数效果的可视化
我们可以绘制模型中变量的边际效应(即重复评分的估计概率)。下面,我们展示了如何不同组合 SEX 和 PPED 不同的概率估计结果。这种方法的优点是概率比几率更容易解释。
Nw %>% dta_gd(SX PE) %>% d\_fddws(Baeo\_inry) %>% plt(ae(x = .vau, y = inatn(SEX, PED))) +
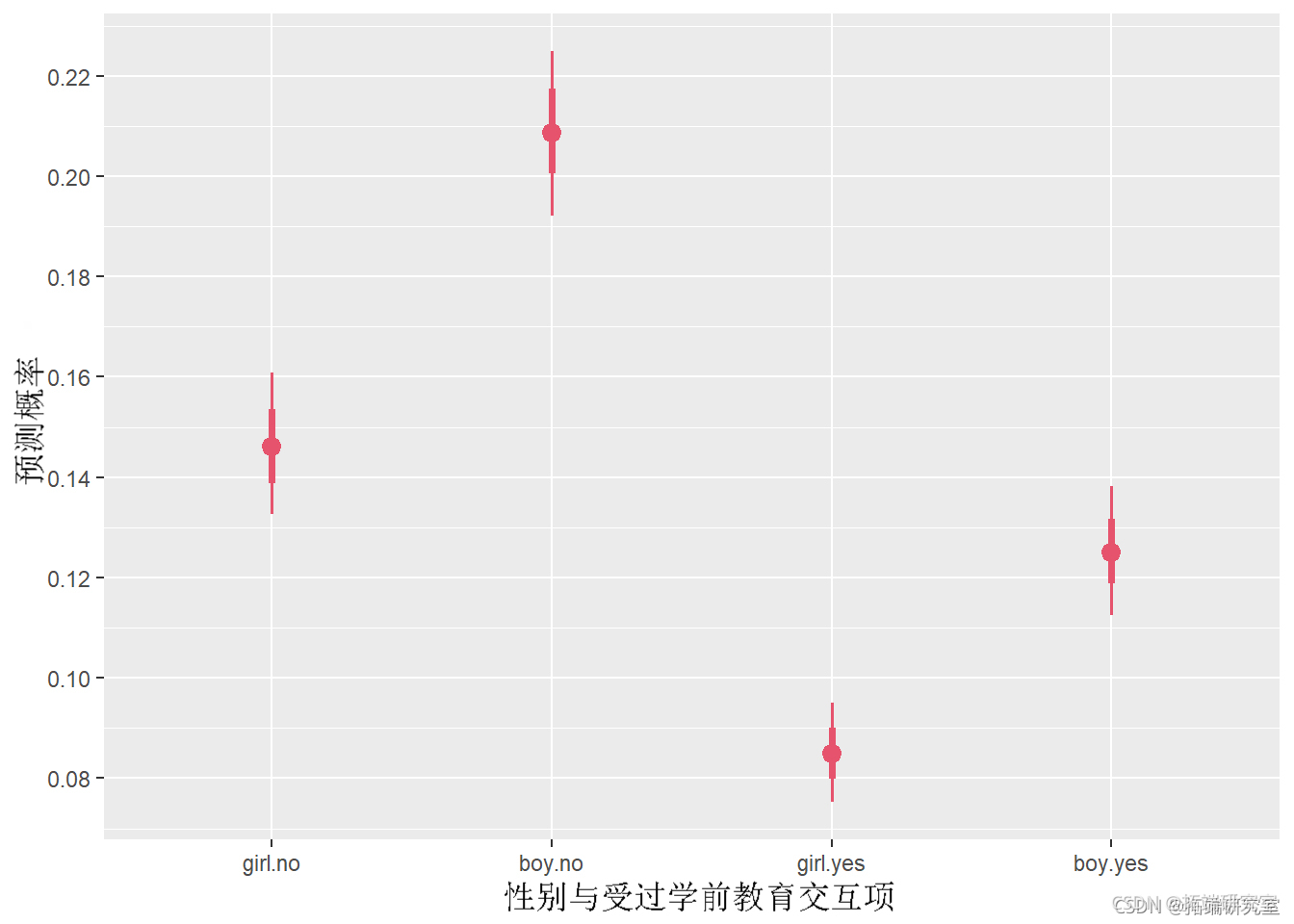
如我们所见,未受过学前教育的男生概率最高(~0.21),其次是未受过学前教育的女孩(~0.15),受过学前教育的男孩(~0.13),最后,是一个受过学前教育的女孩(~0.09)。请注意,估计值的 68%(较粗的内线)和 95%(较细的外线)置信区间都包括在内,以使我们对估计值的不确定性有所了解。
模型评估
我们了解到我们可以使用似然比检验和 AIC 来评估模型的拟合优度。但是,这两种方法不适用于贝叶斯模型。相反,贝叶斯模型利用所谓的 后验预测 P 值 (PPP) 来评估模型的拟合度。此外,许多模型还使用 贝叶斯因子 来量化数据对模型的支持。
另外两个度量 是 正确分类率 和 _曲线下面积(AUC)_。它们与模型无关,也就是说,它们可以应用于频率论和贝叶斯模型。
正确分类率
正确分类的百分比是查看模型与数据拟合程度的有用度量。
#使用\`prdct()\`函数,从拟合的模型中计算出原始数据中学生的预测概率 Prd <- prdct(BadlBay, type = "espnse") Ped <- ilse(Ped\[,1\] > 0.5, 1, 0) CnuMx<- tale(Pre, pul(Nw,REPT)) #\`pull\`的结果是一个向量 #正确的分类率 sm(dag(Cosaix))/sum(Cofinaix)

CMatix

我们可以看到,该模型对所有观测值的85.8%进行了正确分类。然而,仔细观察混淆矩阵可以发现,模型预测所有的观察值都属于 “0 “类,也就是说,所有的学生都被预测为不会留级。考虑到REPEAT变量的多数类别是0(不),该模型在分类中的表现并不比简单地将所有观测值分配给多数类别0(不)更好。
AUC(曲线下面积)
使用正确分类率的替代方法是曲线下面积 (AUC) 度量。AUC 衡量歧视,即测试正确分类那些有和没有目标响应的能力。在当前数据中,目标响应是重复一个等级。我们从“留级”组中随机抽取一名学生,从“不留级”组中随机抽取一名学生。预测概率较高的学生应该是“重复成绩”组中的学生。AUC 是随机抽取的对的百分比,这是正确的。此过程将 AUC 与正确分类率区分开来,因为 AUC 不依赖于结果变量中类别比例的不平衡。值 0.50 表示模型的分类效果并不比机会好。
使用正确分类率的一个替代方法是曲线下面积(AUC)测量。AUC衡量的是分辨力,即测试对因变量进行正确分类的能力。在目前的数据中,目标因变量是留级。我们从 “留级 “组和 “不留级 “组中随机抽取一名学生。预测概率较高的学生应该是 “留级 “组中的学生。AUC是随机抽出的对子的百分比,这一点是真实的。这个程序将AUC与正确分类率区分开来,因为AUC不依赖于结果变量中类的比例的变化。0.50的值意味着该模型的分类效果不比随机好。一个好的模型的AUC分数应该远远高于0.50(最好是高于0.80)。
# 计算用该模型预测类别的AUC Pr <- prdit(Bas\_odl\_iay type="rsone") Pr <- rob\[,1\] Prd <- prition(Prb, as.tor(ull(Ne, REPAT))) auc <- pemneed, easre = "auc") auc

AUC 得分接近 0.60,模型不能很好地区分。
贝叶斯二项式逻辑回归(具有非信息先验)
逻辑回归也可用于对计数或比例数据进行建模。二元逻辑回归假设结果变量来自伯努利分布(这是二项分布的特例),其中试验次数 nn 为 1,因此结果变量只能是 1 或 0。相反,二项逻辑回归假设目标事件的数量服从 n 次试验和概率 q 的二项式分布。通过这种方式,二项逻辑回归允许结果变量采用任何非负整数值,因此能够处理计数数据。
聚集在学校内的个别学生的 信息。通过汇总按学校留级的学生人数,我们获得了一个新数据集,其中每一行代表一所学校,以及有关该学校留级学生比例的信息。该 MSESC (平均得分SES)也对学校的水平; 因此,它可用于预测特定学校留级学生的比例或数量。见下文。
转换数据
Prop <-New %>% gouby(SOLD,MSC) %>% suie(EAT = sum(RPT), TAL = n()) %>% urup()

在这个新的数据集中, REPEAT 指的是留级的学生人数; TOTAL 指特定学校的学生总数。
探索数据
Prop %>% plot(aes(x , y ) + point()
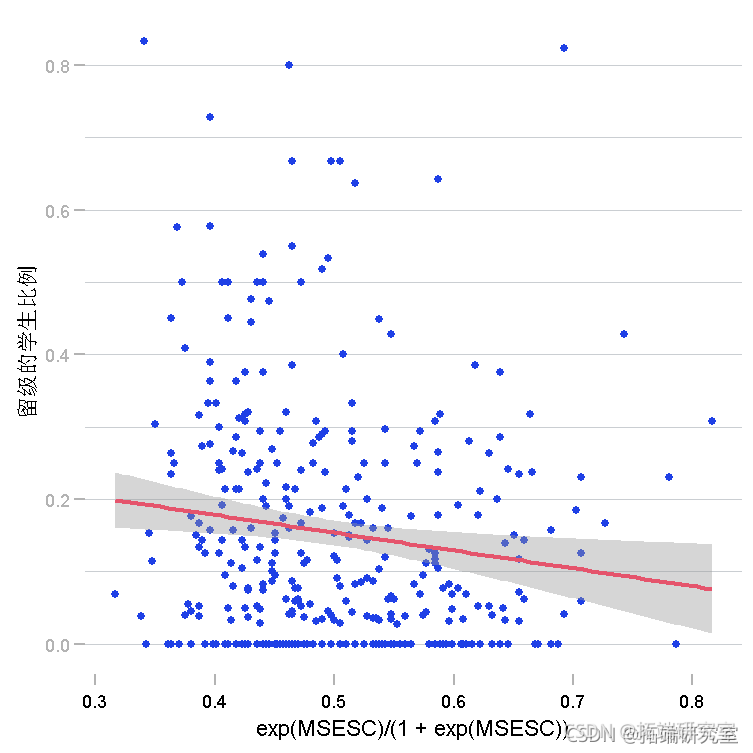
我们可以看到,留级的学生比例与 的逆对数呈(中等)负相关 MSESC。请注意,我们将变量建模 MSESC 为其逆 logit,因为在二项式回归模型中,我们假设线性预测变量的逆 logit 与结果(即事件的比例)之间存在线性关系,而不是预测变量本身与预测变量之间的线性关系结果。
拟合二项 Logistic 回归模型
为了拟合贝叶斯二项逻辑回归模型,我们还使用了brm 与之前的贝叶斯二项逻辑回归模型一样的 函数。但是,有两个不同之处:首先,要在公式中指定结果变量,我们需要指定目标事件数 ( REPEAT) 和包含在 中的试验总数 ( TOTAL) trials(),它们之间用 分隔 |。此外, family 应该是“二项式”而不是“伯努利”。
ay_Moe(REAT | rias(TTAL) ~ SEC, daa = Pop, inillnk "logt"))

summary

频率模型(用于比较):
glm(fla =ind(PEAT, TAL-PET) ~ SS, famiy = inal(lgit), dta =Prop)

我们可以看到贝叶斯和频率二项式逻辑回归模型之间的模型估计非常相似。请注意,为了使本教程更简短,我们跳过了检查模型收敛的步骤。您可以使用我们之前展示的相同代码(使用二元逻辑回归模型)来检查该模型的收敛性。
解释
二项式回归模型中的参数解释与二项逻辑回归模型中的参数解释相同。我们从上面的模型总结中知道,一所学校的平均 SES 分数与该学校学生留级的几率呈负相关。为了增强可解释性,我们再次计算 的指数系数估计 MSESC。由于 MSESC 是一个连续变量,我们可以对指数MSESC 估计进行标准化 (通过将原始估计与变量的 SD 相乘,然后对结果数字取幂)。
exp(fxef(Bodlrp)\[2,-2\]*sd(pll(_p,MSC), n.rm = T))

我们可以看到,随着 的 SD 增加 MSESC,学生留级的几率降低了大约 (1 – 85%) = 15%。“Q2.5”和“Q97.5”分别指不确定区间的下限和上限。该置信区间不包含零,表明该变量可能有意义。
我们可以将 的效果可视化 MSESC。
reraw(btrct, SSC) %>% grp(MSESC) %>% sume(ped_m = mean(ed,ar = R re_lw = qantle(ped,po = 0.025), rd_hgh = quatle(pd, prb = 0.975)) %>% plt(as(x = SC, y = pedm)) + line() + gmn(es(ymn = pe_ow,yma = redig), aha=.2) +
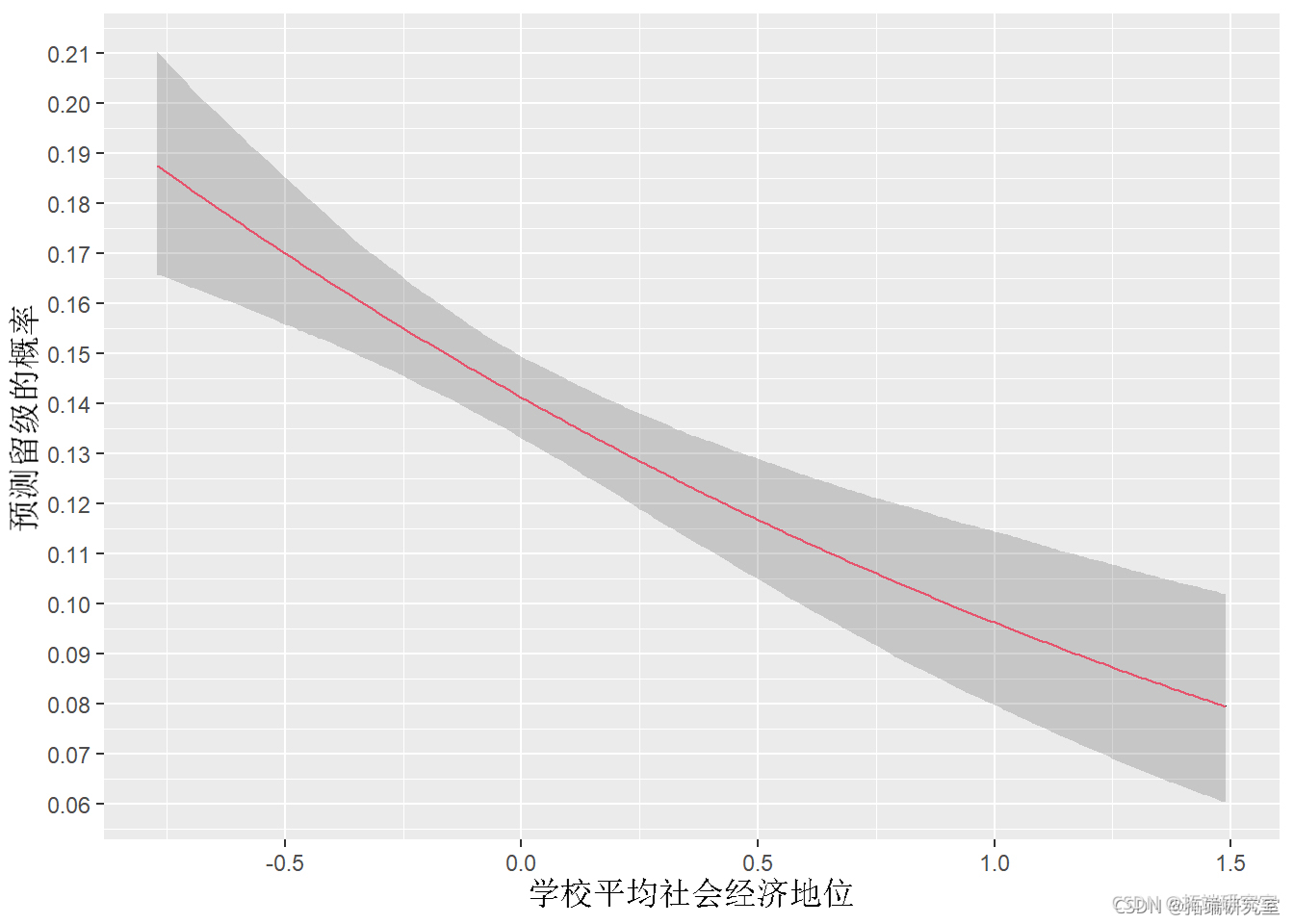
上图显示了MSESC 对学生留级概率的预期影响 。保持其他一切不变,随着 MSESC 增加,学生留级的概率降低(从 0.19 到 0.08)。灰色阴影区域表示每个 值处预测值的 95% 置信区间 MSESC。
模型评估
与贝叶斯二元逻辑回归模型类似,我们可以使用PPPS和贝叶斯系数(本教程中没有讨论)来评估贝叶斯二元逻辑回归模型的拟合度。正确分类率和AUC在这里不适合,因为该模型不涉及分类。
贝叶斯多层次二元逻辑回归(具有非信息先验)
前面介绍的贝叶斯二元逻辑回归模型仅限于对学生层面的预测因素的影响进行建模;贝叶斯二元逻辑回归仅限于对学校层面的预测因素的影响进行建模。为了同时纳入学生层面和学校层面的预测因素,我们可以使用多层次模型,特别是贝叶斯的多层次二元逻辑回归。
除了上述动机之外,还有更多的理由来使用多层次模型。例如,由于数据是在学校内聚类的,来自同一学校的学生很可能比来自其他学校的学生更相似。正因为如此,在一所学校,一个学生留级的概率可能很高,而在另一所学校,则很低。此外,即使是结果(即留级)和预测变量(如性别、学前教育、SES)之间的关系,在不同的学校也可能不同。还要注意的是,MSESC变量中存在缺失值。使用多层次模型可以适当地解决这些问题。
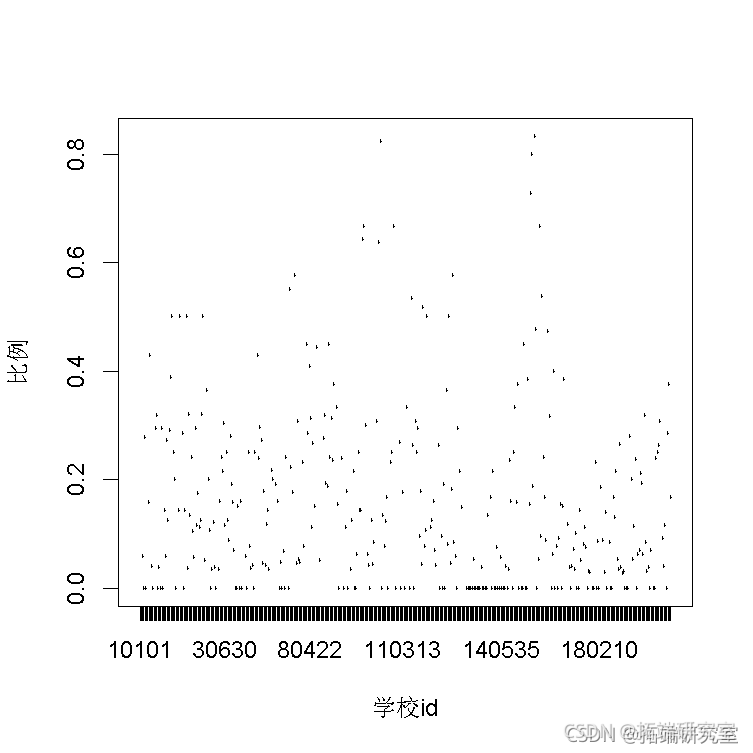
以下图为例。该图显示了各个学校留级学生的比例。我们可以看到不同学校之间的巨大差异。因此,我们需要多层次模型。
Edu %>% grop_(ID) %>% sumrie(RP = sum(PA)/n()) %>% plt()
我们还可以绘制SEX 和 REPEAT ,SCHOOLID之间的关系 ,查看性别和留级之间的关系是否因学校而异。
Euew %>% utt(SX = ifelse(EX == "boy", 1, 0)) %>% plt(es(x = SE, y = REAT)) + pint(alpha = .1)+ ooth(mehod = "glm", se = F, hd.s= lsily = "binomial"))
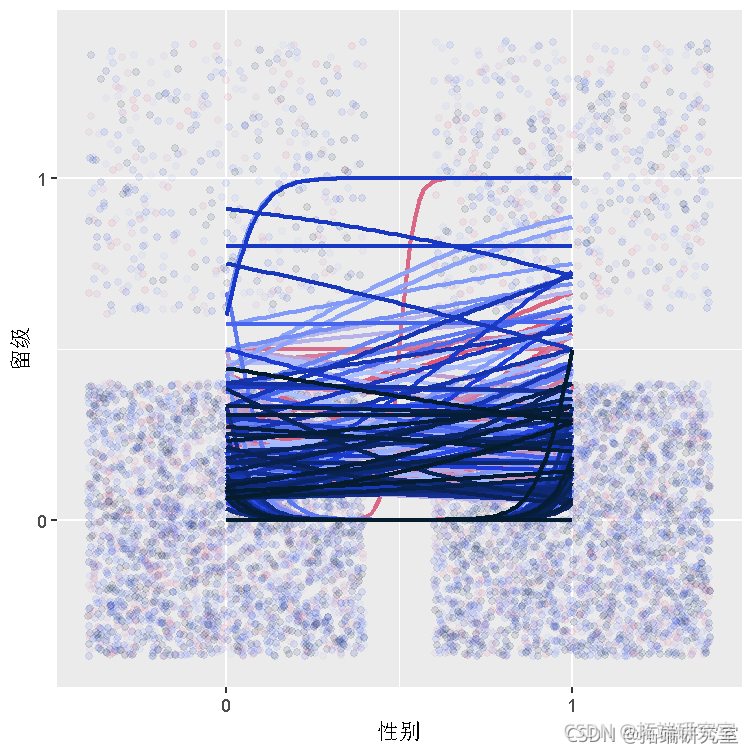
在上面的图中,不同的颜色代表不同的学校。我们可以看到,不同学校的SEX和REPEAT之间的关系似乎有很大不同。
我们可以为PPED 和 REPEAT绘制相同的图 。
due %>% tat(PED = ifelse(PED == "yes", 1, 0)) %>% pot(as(x = PP, y = RPT, cor =a.fcor(ID)) + goi(lha=.1, )+ goth(method = "glm", ehog = lst(family = "binomial")) +
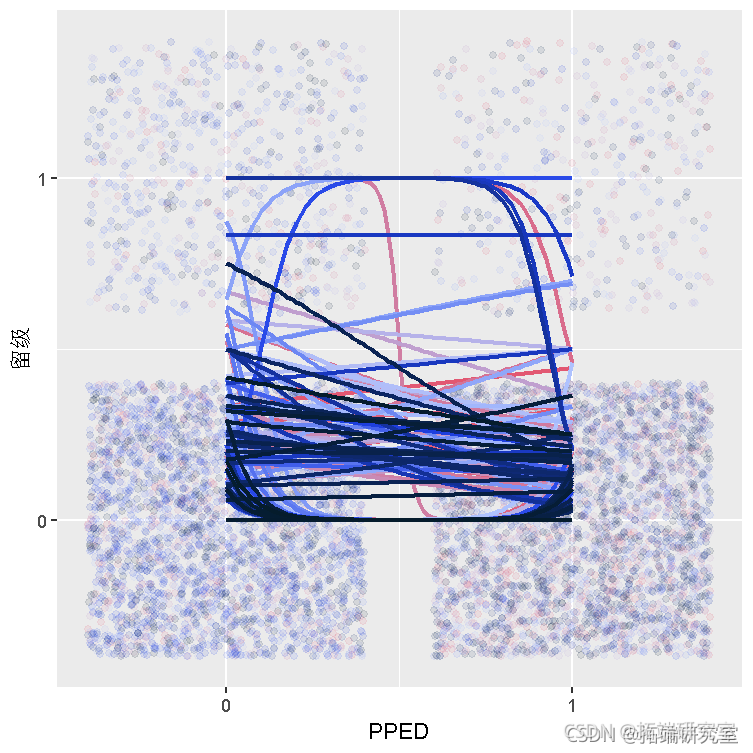
PPED 和 之间的关系 REPEAT 似乎也因学校而异。但是,我们也可以看到,大多数关系遵循下降趋势,从 0(未受过教育)到 1(受过教育),表明PPED 和 REPEAT之间存在负相关关系 。
由于上述观察,我们可以得出结论,需要在当前数据中进行多层次建模,不仅具有随机截距 ( SCHOOLID),而且还具有SEX 和 的 潜在随机斜率 PPED。
中心变量
在拟合多层次模型之前,有必要使用适当的中心化方法(即大均值中心化或簇内中心化)对预测因子进行中心化,因为中心化方法对模型估计的解释很重要。根据Enders和Tofighi(2007)的建议,我们应该对第一层次的预测因子SEX和PPED使用组内中心化,对第二层次的预测因子MSESC使用平均值中心化。
Euee <- New %>% group_by(ID) %>% muae(SEX - mean(SE), PED - mean(PED)) %>% uou() %>% muate( ME - mean(MEC, na.rm = T))

仅截距模型
为了指定多层次模型,我们再次使用 包中的 brm 函数 brms。请注意,随机效应项应包含在括号中。此外,在括号内,随机斜率项和聚类项之间应以 隔开 |。
我们首先指定一个仅截距模型,以评估数据聚类结构的影响。我们将跳过模型收敛诊断的步骤。
BaeselMti(RPAT ~ 1 + (1|SOLID), data famly = beouli(link = "logt"

下面我们计算仅截距模型的 ICC(类内相关性)。请注意,对于非高斯贝叶斯模型(例如逻辑回归),我们需要设置“ppd = T”,以便方差计算基于后验预测分布。
icc(BylMunrept, pd = T)

0.29 的方差比(与 ICC 相当)意味着结果变量中 29% 的变异可以由数据的聚类结构来解释。这提供了证据,表明与非多层次模型相比,多层次模型可能会对模型估计产生影响。因此,多层次模型的使用是必要的。
完整模型
按部就班地建立多层次模型是一个好的做法。然而,由于本教程的重点不是多层次模型,我们直接从仅有的截距模型到我们最终感兴趣的完整模型。在完整模型中,我们不仅包括SEX、PPED和MSESC的固定效应项和一个随机截距项,还包括SEX和PPED的随机斜率项。请注意,我们指定family = bernoulli(link = “logit”),因为这个模型本质上是一个二元逻辑回归模型。
baysMoel(RPET ~ EX + PED + SESC + (1 + EX + PPD|ID), data famy = brnuli(lnk = "loit"))
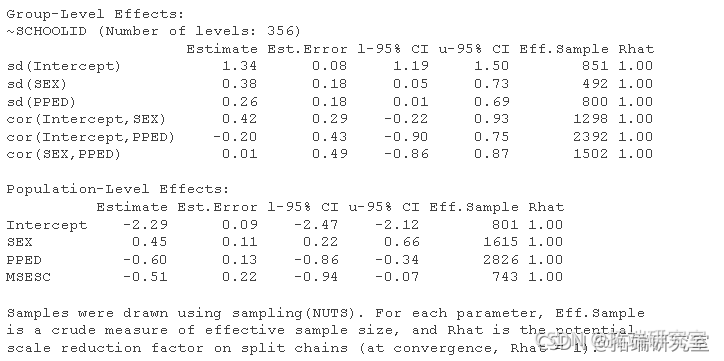
summary(BaeMil)
我们可以绘制相关模型参数估计的密度。
plot(ByodlMtil, prb = 95)
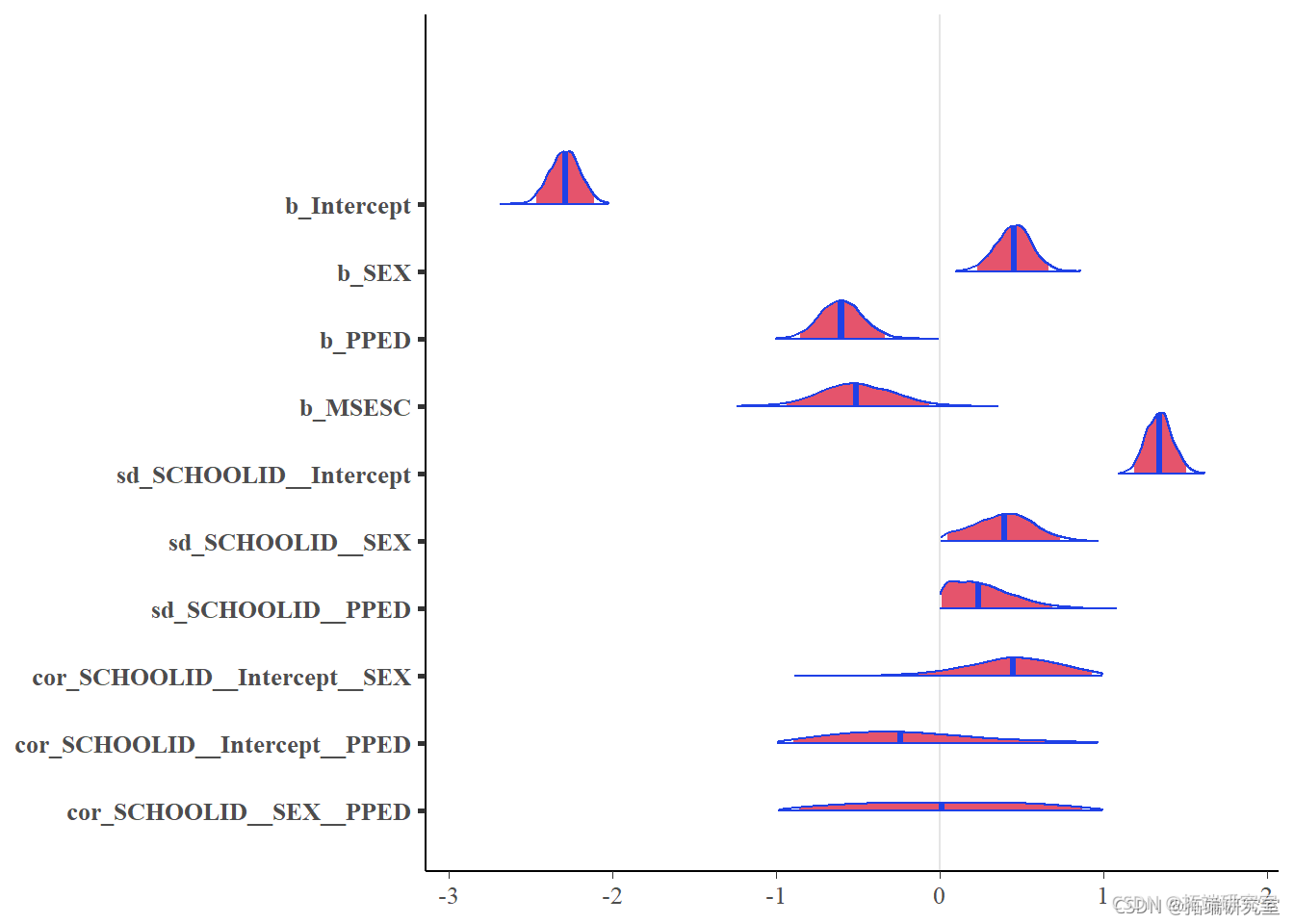
结果(与固定效应有关)与之前贝叶斯二元逻辑回归和二元逻辑回归模型的结果相似。在学生层面上,性别对学生留级的几率有正向影响,而PPED有负向影响。在学校层面上,MSESC对结果变量有负面的影响。在三个预测因子中,SEX和PPED的置信区间(由密度中的浅蓝色阴影区域表示)显然不包含零。因此,它们应该被视为有意义的预测因素。相反,MSESC尽管有95%的可信区间不含零,但可信区间的上界非常接近于零,其密度只包含零。正因为如此,MSESC可能是一个比SEX和PPED更不相关的预测因子。
现在让我们看看随机效应项 ( sd(Intercept), sd(SEX) 和 sd(PPED))。图中的密度 sd(Intercept) 明显远离零,表明在模型中包含此随机截距项的相关性。的随机斜率方差SEX 为0.382=0.140.382=0.14, 随机斜率方差 PPED 为0.262=0.070.262=0.07。这两种差异都不可忽视。但是,如果我们看一下密度图,两者的置信区间的下限 sd(SEX) 和 sd(PPED) 非常接近零,并且它们的密度也没有明确的从零分开。这表明可能不需要包括这两个随机斜率项。
我们还可以绘制跨学校的随机效应项。
#提取所有随机效应项的后验分布 RdEffct <- rf(aoFl) #提取 "sd(Intecpt) "的后验分布 r_ec <- dRf$CI\[, , 1\] %>%。 abbe() %> roton(var = "ID") %>% uae(Vrible = "d(Inercpt)") #提取\`sd(SEX)\`的后验分布。 r_ <- dam$OD\[, , 2\] %>%>。 astle() %>%。 rnlmn(var = "ID") %>% mae(Vaiae = "sd(SEX)") #提取\`sd(PPED)\`的后验分布 r_ED <-atdSH, 3\] %>%>。 ate() %>%。 rotcnr = ID") %>% ute(Vaiale = "sdPE)") #绘图 r_ntct %>% bdows(r_EX) %>% biws(_PED) %>% mat(Coro= ifese(Q2.5*Q97.5 > 0, "no", "yes") ) %>% pot() + goint() + erbr(as(yin=Q2.5, ymx=Q97.5))
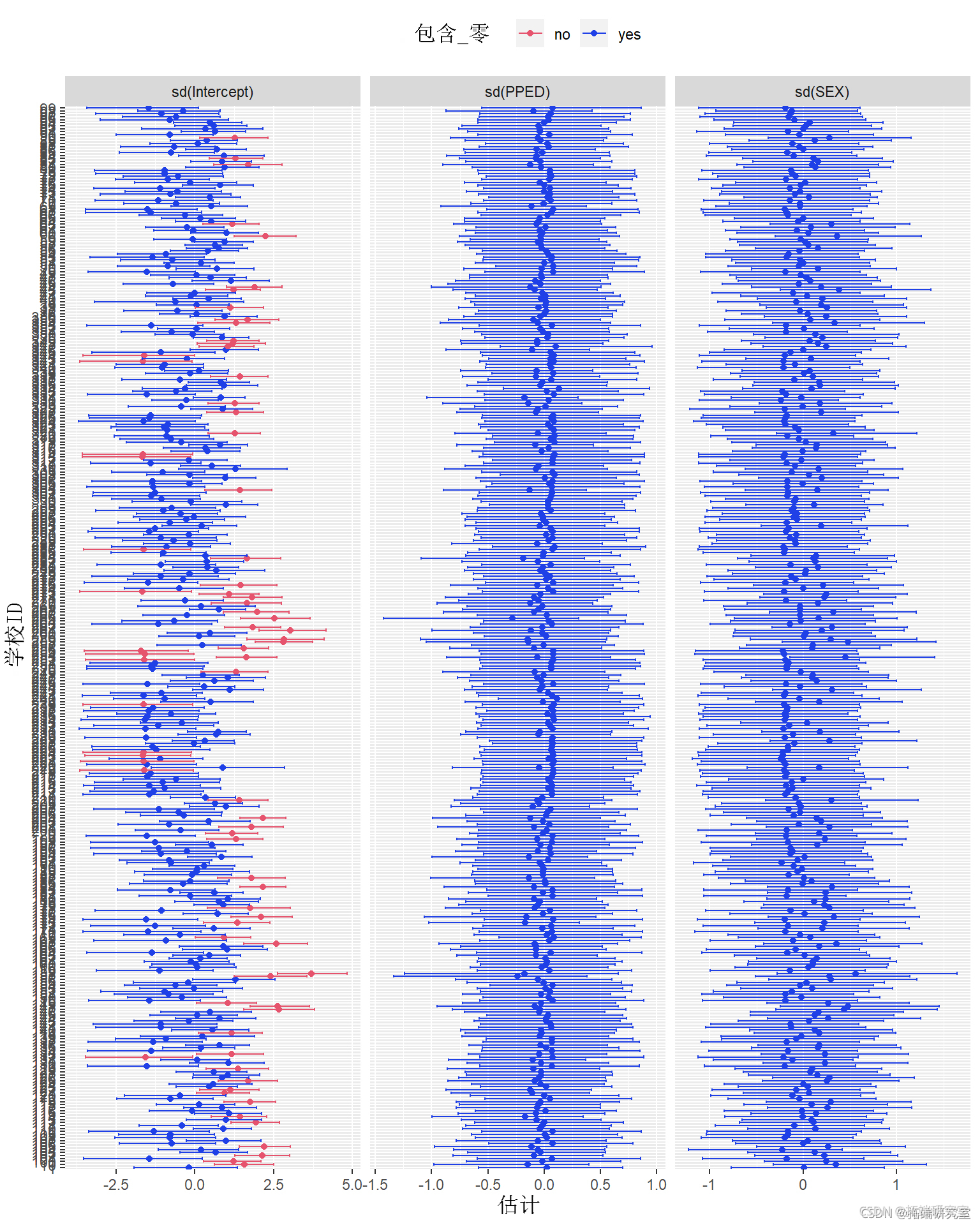
同样,我们可以看到随机截距项 ( sd(Intercept))的后验分布在不同学校之间有很大的差异。他们中的很多人也远离零。因此,我们可以得出结论,包含随机截距是必要的。相比较而言,所有的后验分布的 sd(SEX) ,并 sd(PPED) 经过零,这表明有可能是没有必要在模型中包含两个随机斜率。
为了解释固定效应项,我们可以计算指数系数估计值。
##分类变量:SEX和PPED exp(fif(BeoMiF)\[-4,-2\])

##连续的变量:MSESC exp(fxf(BelFl)\[4,-2\]*sd(ul(i_o ))

我们可以看到,SEX、PPED和MSESC的影响与之前的模型结果非常相似。
参考
Sing, T., Sander, O., Beerenwinkel, N. & Lengauer, T. (2005)。 ROCR:可视化 R. 生物信息学中的分类器性能,21 (20),第 7881 页。 http://rocr.bioinf.mpi-sb.mpg.de
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载
2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载 2026年人工智能AI未来报告:智能体、元宇宙、教育、商业化落地|附400+份报告PDF、数据、可视化模板汇总下载
2026年人工智能AI未来报告:智能体、元宇宙、教育、商业化落地|附400+份报告PDF、数据、可视化模板汇总下载 LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
