回归分析是评估结果变量与一个或多个风险因素或混杂变量之间关系的相关技术。结果变量也被称为应答或因变量，风险因素和混杂因素被称为预测因子或解释性或独立变量。在回归分析中，因变量表示为“ y”，自变量表示为“ x””。

相关分析

在相关分析中，我们估计了样本相关系数，更具体地说是Pearson乘积矩相关系数。样本相关系数，表示为r，

介于-1和+1之间，并量化两个变量之间的线性关联的方向和强度。两个变量之间的相关性可能是正的（即一个变量的较高水平与另一个变量的较高水平相关）或负的（即一个变量的较高水平与另一个变量的较低水平相关）。

相关系数的符号表示关联的方向。相关系数的大小表示关联的强度。

例如，r = 0.9的相关性表明两个变量之间强烈的正相关，而r = -0.2的相关性表明弱相关性。接近于零的相关性表明两个连续变量之间没有线性关联。

需要注意的是，两个连续变量之间可能存在非线性关联，但相关系数的计算不会检测到这一点。因此，在计算相关系数之前仔细评估数据总是很重要的。图形显示对探索变量之间的关联特别有用。

下图显示了四个假设情景，其中一个连续变量沿着X轴绘制，另一个沿着Y轴绘制。

​

情景1描述了强烈的正相关（r = 0.9），类似于我们可以看到的婴儿出生体重与出生体重之间的相关性。

情景2描述了我们可能期望看到的年龄与体重指数（其随着年龄增加而增加）之间的较弱关联（r = 0,2）。

情景3可能表明青少年媒体暴露的程度与青少年发起性行为的年龄之间缺乏联系（r大约为0）。

情景4可能描述了每周有氧运动小时数与体脂百分比之间通常观察到的强烈负相关（r = -0.9）。

示例 – 妊娠期和出生体重的相关性

一项小型研究涉及17名婴儿，以调查出生时的胎龄（以周为单位）和出生体重（以克为单位）之间的关联。

​

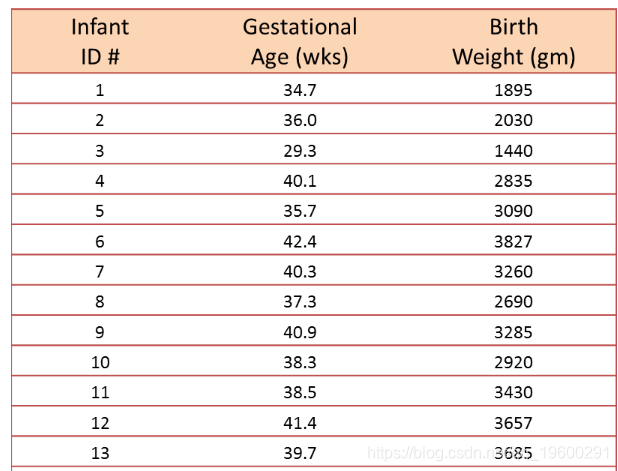
我们希望估计胎龄与婴儿出生体重之间的关系。在这个例子中，出生体重是因变量，孕龄是自变量。因此y =出生体重和x =胎龄。数据显示在下图中的散点图中。

​

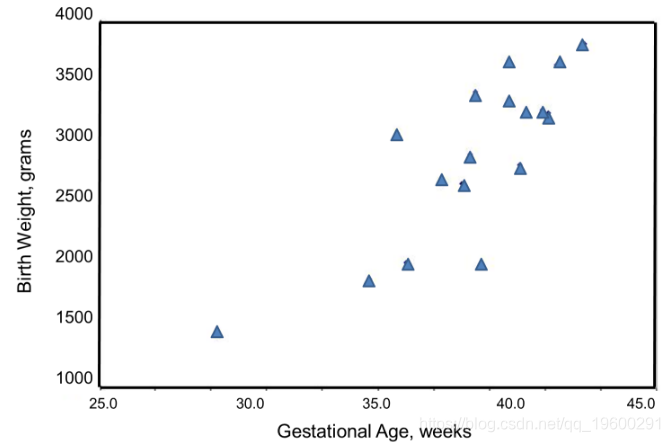
每个点代表一个（x，y）对（在这种情况下，孕周，以周为单位，出生体重以克为单位）。请注意，独立变量位于水平轴（或X轴）上，因变量位于垂直轴（或Y轴）上。散点图显示胎龄与出生体重之间存在正向或直接关联。胎龄越短的婴儿出生体重越低，胎龄越长的婴儿出生体重越高的可能性越大。

​

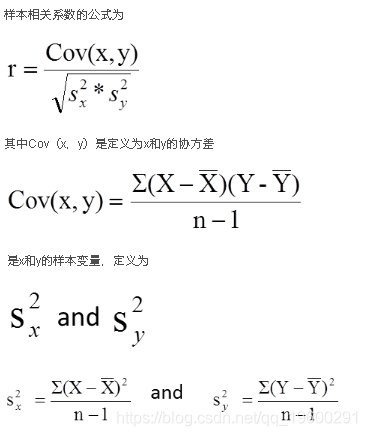
x和y的方差测量其各自样本均值附近的x分数和y分数的变化性（

​

正如我们对孕龄所做的那样计算出生体重的方差，如下表所示。

​

​

​

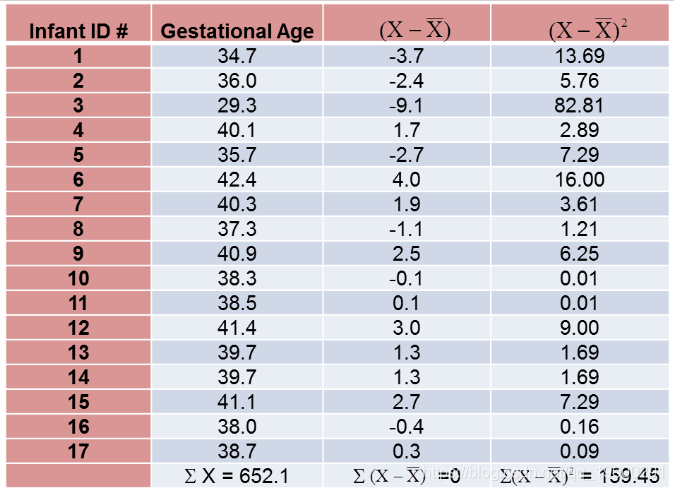
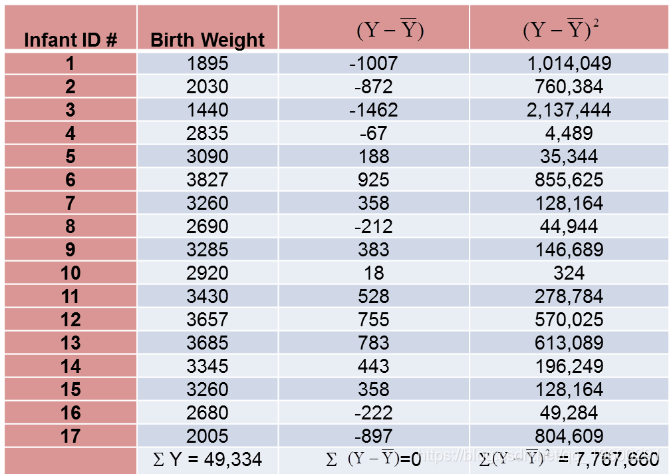
计算总结如下。请注意，我们只是简单地将平均孕龄和出生体重的偏差从上表中的两张表中复制到下表中并进行相乘。

​

​

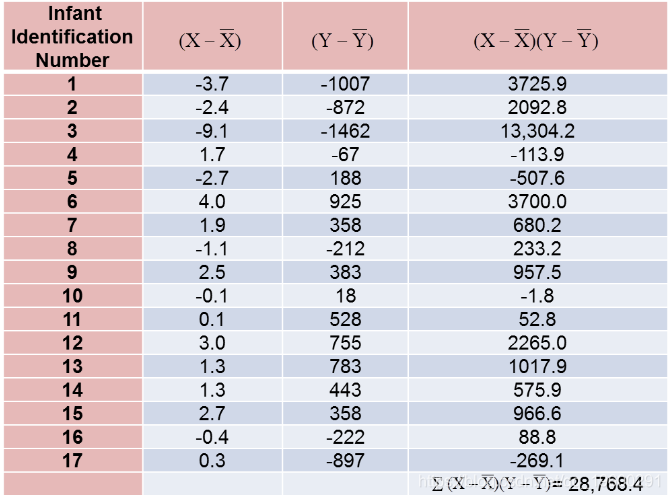
毫不奇怪，样本相关系数表明强正相关。

正如我们所指出的，样本相关系数范围从-1到+1。在实践中，对于正面（或负面）关联而言，有意义的相关性（即临床上或实际上重要的相关性）可小至0.4（或-0.4）。还有统计测试来确定观察到的相关性是否具有统计显着性（即统计显着性不同于零）。