
为了用R来处理网络数据,我们使用婚礼数据集。
最近我们被客户要求撰写关于复杂网络分析的研究报告。
复杂网络是由数量众多的节点和节点之间的连接边组成的网络结构。
在复杂网络中,节点可以代表各种实体,如人、计算机、生物细胞等,连接边则表示节点之间的关系或相互作用。复杂网络具有一些独特的性质,比如小世界特性、无标度特性等。
例如,社交网络就是一种复杂网络,其中的人是节点,人与人之间的关系如朋友关系、同事关系等是连接边。
在复杂网络分析中,可以研究网络的结构、功能、动态演化等方面,以更好地理解和解释各种复杂系统的行为和特性。
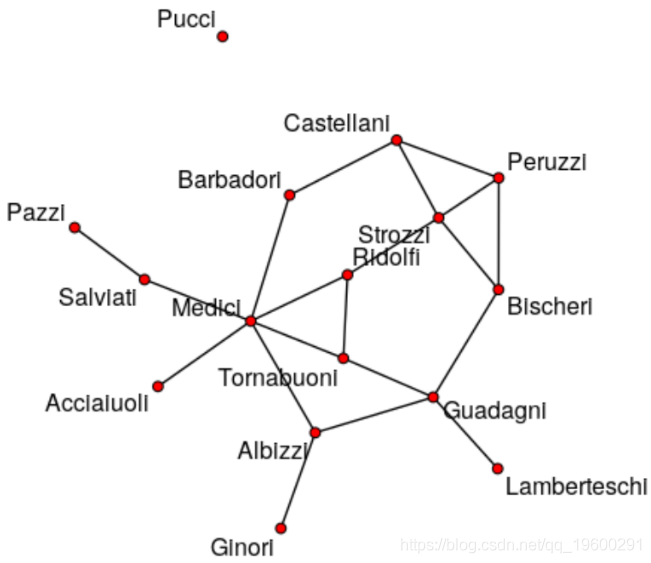
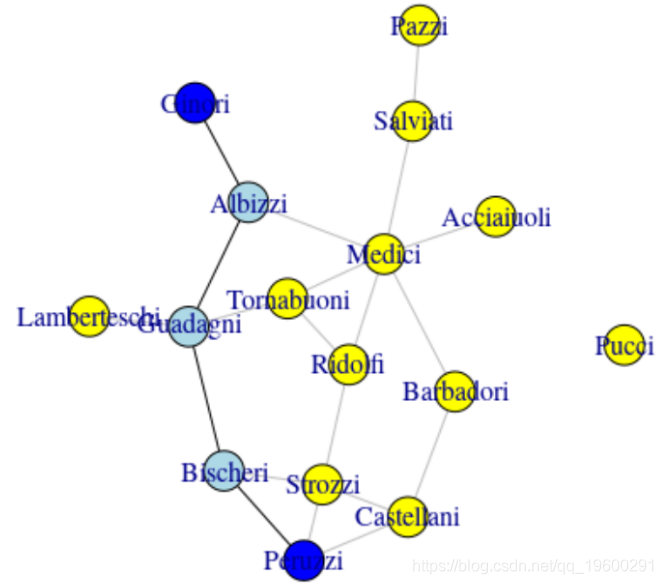
导入数据后进行简单的网络图可视化
> nflo=network(flo,directed=FALSE)
> plot(nflo, displaylabels = TRUE,
+ boxed.labels =
+ FALSE)社团检测通常是指将网络中联系紧密的部分找出来,这些部分就称之为社团,那么也可以认为社团内部联系稠密,而社团之间联系稀疏 [1]。显而易见,其中有一个非常重要的点,稠密是如何定义的。不管现在想到的定义是什么,但都包含顶点,边,度,或许还有路径这些字眼,它们有一个共同的特征–网络的结构。所以,社团检测侧重于找到网络中联系紧密的部分,而经常忽略节点的属性(attributes)[2]。
聚类,顾名思义是将属于同一类的目标聚在一起,通常在聚类之前我们是不知道目标有哪些类型,这也是一种典型的无监督学习方法。那么现在来想想我们熟知的聚类方法:k-means,层次聚类等。其中,最核心的一个部分是计算两个目标之间的距离(或者称为相似度),距离近则它俩是一类,距离远,那就自成一派,或者去找其它距离近的。当然,距离近只是其中一种方法,还有距离远或者怎么样,就看自己的判断。判断标准不是讨论的重点,重点是如何计算距离。欧式距离,曼哈顿距离,余弦相似度等,都是直接用目标特征构成的向量来计算的,没有考虑目标的边,度。所以,聚类侧重于找到一堆属性相似的目标,从而忽略了目标与目标之间的联系。
两者之间的关系已经很清楚啦, 社团检测和聚类存在区别,但是呢,两者又是可以结合起来的。比如,我们现在有一个网络,只知道顶点和边的情况,顶点的属性是未知的。那么在做社团检测的时候,可以将顶点与顶点之间的关系构成一个邻接矩阵,通过一系列变化或者就这个邻接矩阵而言,将每个行看作一个属性,每个列看作目标,就可以很轻松的转为聚类,用聚类的方法求解。当邻接矩阵高维时,还可以先做降维处理。所以,两者并没有完全独立,只是考虑的角度不同,可以结合使用。现在社交网络方向有一个很热门的就是用attributes来辅助进行社团检测,是对传统的社团检测和聚类方法的一种改进,两者优势互补。
参考文献:
[1]Newman M E, Girvan M. Finding and evaluating community structure in networks.[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2004, 69(2):026113.
[2]Yang J, Mcauley J, Leskovec J. Community Detection in Networks with Node Attributes[J]. 2014:1151-1156.
下一步是igraph。由于我们有邻接矩阵,因此可以使用它
graph_from_adjacency_matrix(flo,
+ mode = "undirected")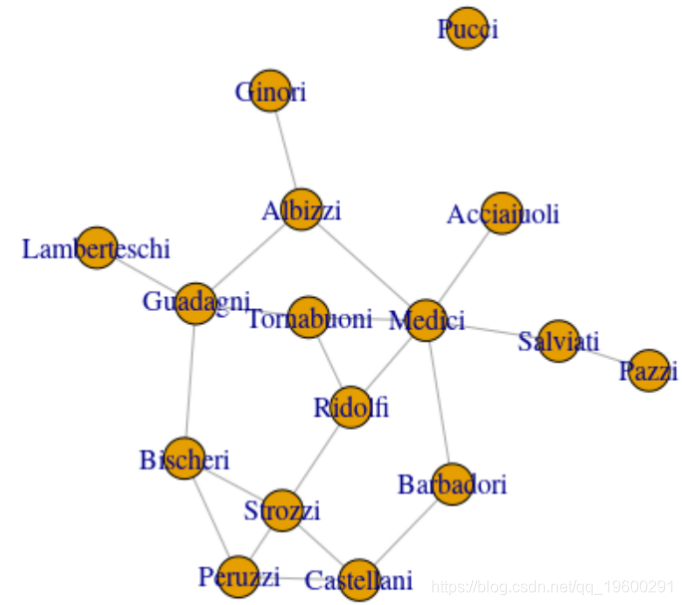
我们可以在两个特定节点之间获得最短路径。我们给节点赋予适当的颜色
all_shortest_paths(iflo,
)
> plot(iflo)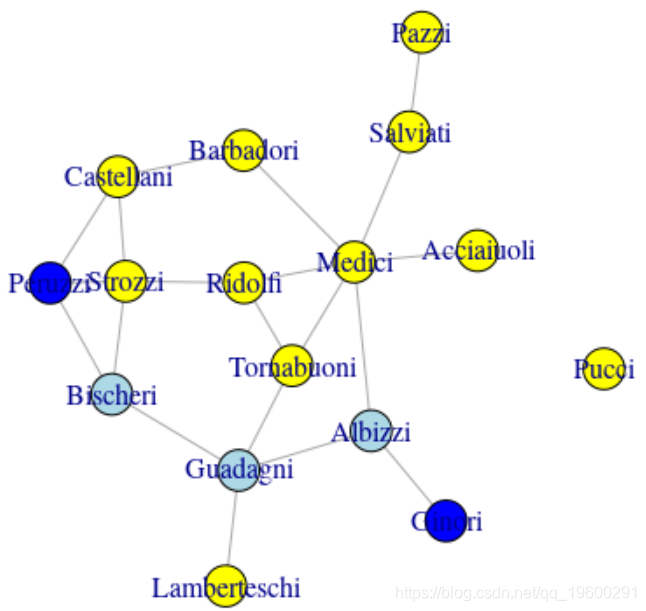
我们还可以可视化边,需要从输出中提取边缘
> lins=c(paste(as.character(L)[1:4],
+ "--"
+ as.character(L)[2:5] sep="" ,
+ paste(as.character(L) 2:5],
+ "--",
> E(ifl )$color=c("grey","black")[1+EU]
> plot(iflo)> library( networkD3 )
> simpleNetwork (df)下一个问题是向网络添加一个顶点。最简单的方法是通过邻接矩阵实现概率
> flo2["f","v"]=1
> flo2["v","f"]=1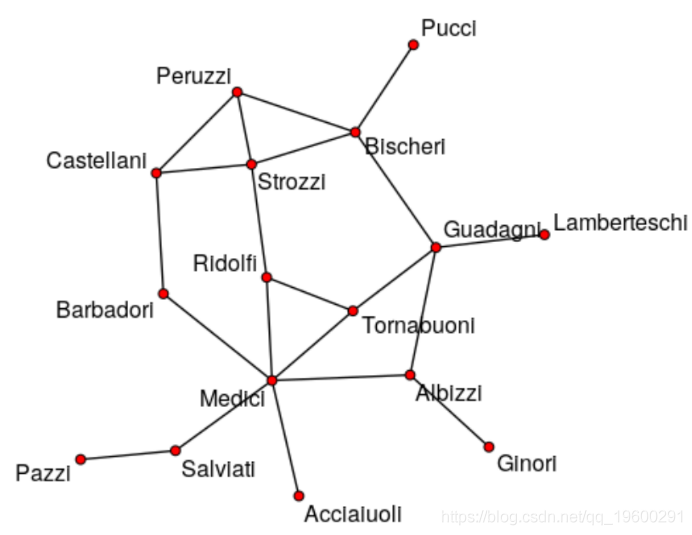

想了解更多关于模型定制、咨询辅导的信息?
然后,我们进行集中度测量。
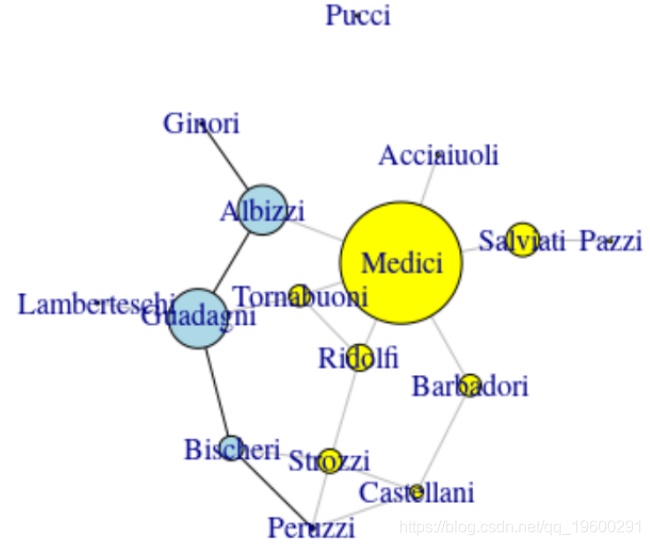
目的是了解它们之间的关系。
betweenness(ilo)
> cor(base)
betw close deg eig
betw 1.0000000 0.5763487 0.8333763 0.6737162
close 0.5763487 1.0000000 0.7572778 0.7989789
deg 0.8333763 0.7572778 1.0000000 0.9404647
eig 0.6737162 0.7989789 0.9404647 1.0000000可以使用层次聚类图来可视化集中度度量
hclust(dist( ase ,
+ method="ward")
查看集中度度量的值,查看排名
> for(i in 1:4) rbase[,i]=rank(base[,i])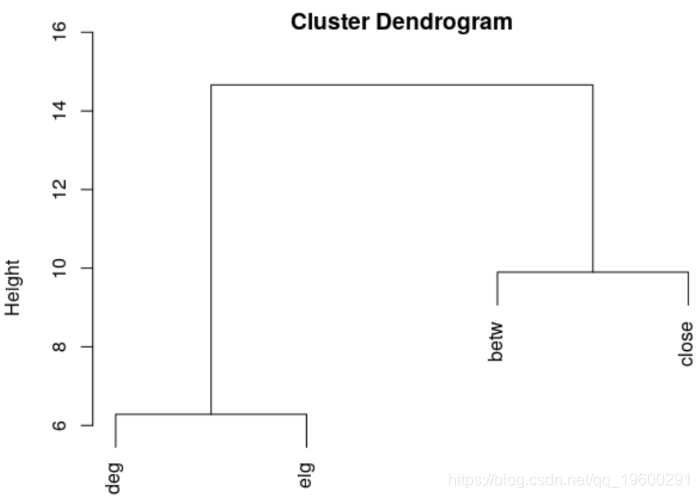
在此,特征向量测度非常接近顶点的度数。
最后,寻找聚类(以防这些家庭之间爆发战争)
> kc <- fastgreedy.community ( iflo )在这里,我们有3类
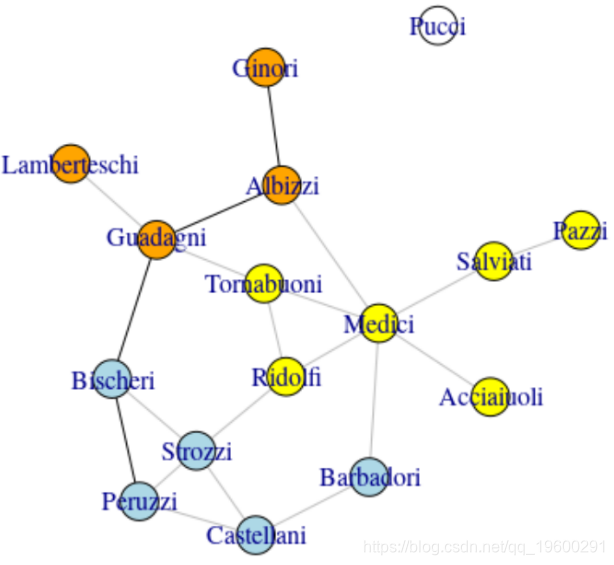
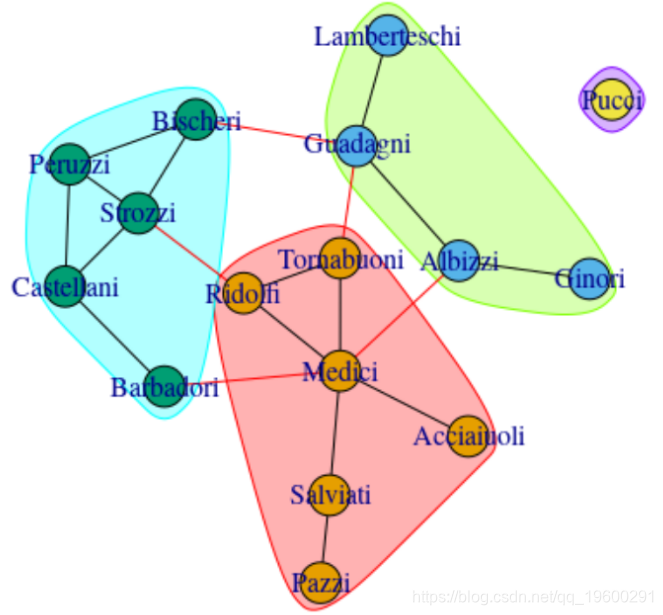
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化
Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 Python与R语言用XGBOOST、NLTK、LASSO、决策树、聚类分析电商平台评论文本信息数据集
Python与R语言用XGBOOST、NLTK、LASSO、决策树、聚类分析电商平台评论文本信息数据集
