降维是在我们处理包含过多特征数据的大型数据集时使用的，提高计算速度，减少模型大小，并以更好的方式将巨大的数据集可视化。
这种方法的目的是保留最重要的数据，同时删除大部分的特征数据。
在这个教程中，我们将简要地学习如何用Python中的稀疏和高斯随机投影以及PCA方法来减少数据维度。读完本教程后，你将学会如何通过使用这些方法来降低数据集的维度。本教程包括。
可下载资源
1. 随机投影 （Random Projection）
首先，这是一种降维方法。之前已经介绍过相对普遍的PCA的降维方法，这里介绍另一种降维方法Random Project。相比于PCA，他的优势可以这样说：
Random Projection与PCA不一样，其操作简单，只要构建一个投影矩阵即可，而PCA降维还要做SVD，计算开销比较大
1.1 Brief Introduction
随机投影的理论依据是J-L Lemma，公式的核心思想总结一句话就是：在高维欧氏空间里的点集映射到低维空间里相对距离得到某误差范围内的保持。至于为什么要保持，主要是很多机器学习算法都是在以利用点与点之间的距离信息展开计算分析的(如k-means)。
1.2 Johnson–Lindenstrauss lemma
其实并不想这么数学，但是这么重要的定理不说不行。
定理表示：对于任意一个样本大小为m的集合，如果我们通过随机投影将其维度降到一个合适的范围 n>8ln(m)/ϵ2n>8ln(m)/ϵ2 内，那么我们将以较高的概率保证投影后的数据点之间的距离信息变化不大。这样我们在做K-mean之类的算法时，就可以先将高维度的数据利用随机投影进行降维处理，然后在执行算法。
上式中，ff为投影到n维空间的正交投影。显然，这样的正交投影操作通常会减少样本点之间的平均距离。该定理Lemma可以看成这样操作：首先，你通过算法获得随机投影，这可能减少平均距离，然后你scale up这个距离，以便平均距离返回到其先前的值。 这个操作将不再是一个NP-hard问题，时间复杂度降为多项式复杂度。
1.3 Method
介绍完JL Lemma，接下来就简单了。如果Xd×NXd×N 是d维的原始样本矩阵，那么XRPk×N=Rk×dXd×NXk×NRP=Rk×dXd×N是降维后的k维样本矩阵。这个计算过程十分简单，生成随机矩阵RR且将XX映射从dd为到kk维空间中的时间复杂度为O(nkd)O(nkd)。
1.4 高斯随机投影 Gaussian random projection
可以使用高斯分布生成随机矩阵 RR。随机矩阵的第一行是从Sd−1Sd−1均匀选择的随机单位向量，第二行是来自与第一行正交的空间的随机单位向量，第三行是来自与前两行正交的空间的随机单位矢量，依此类推。 在这种选择 RR 的方式中，RR 是正交矩阵（其转置的倒数），并且满足以下属性：
-
球对称(Spherical symmetry)：对于任何正交矩阵A∈O(d)A∈O(d)，RARA 和 RR 具有相同的分布。
-
正交性：R的行彼此正交。
-
R的行是单位长度向量。
要讨论高斯随机投影为什么有效，我们需要先来讨论下一个核心问题，高斯投影是否可以从理论上保证投影降维前后，数据点的空间分布距离基本保持不变呢？这个问题其实可以等价于证明另一个问题，即高斯投影能否做到将高维空间的点均匀的投影到低维空间中，如果能做到这一点，那么我们也可以证明其具备“投影降维前后，数据点的空间分布距离基本保持不变”的能力。
我们来考虑一个采样问题，就是怎样在高维单位球体的表面上均匀的采样。首先，考虑二维的情况，就是在球形的周长上采样。我们考虑如下方法：第一，先在一个包含该圆形的外接正方形内均匀的采样；第二，将采样到的点投影到圆形上。具体地说就是，第一，先独立均匀的从区间[−1,1]（我们假设圆形跟正方形的中心点都在原点）内产生两个值组成一个二维的点(x1,x2)；第二，将该二维点投影到圆形上。例如，如下图所示，如果我们产生点是图中的A,B两点，那么投影到圆形上就是C点，如果产生的是点D，那么投影到圆形上就是E点。但是，用这样的方法得到点在圆形上并不是均匀分布的，比如产生C点的概率将大于产生E点概率，因为可以投影到C点对应的那条直线比E点对应的那条直线要长。解决的办法是去掉圆形外面的点，也就是如果我们首先产生的点在圆形外的话（比如点B），那么我们就丢弃该点，重新在产生，这样的话产生的点在圆形上是均匀分布的。
那么，我们能否将此方法扩展到高维的情况下呢？答案是不行的。因为在高维的情况下球与正方体的体积比将非常非常小，几乎接近于零。也就是我们在正方体内产生的点几乎不可能落到球体内部，那么也就无法产生有效的点。那么，在高维的球体上，我们应该怎样才能产生一个均匀分布与球体表面的点呢？答案是利用高斯分布。即将上述第一步改成：以均值为零方差为1的高斯分布独立地产生d个值，形成一个d维的点x=(x1,x2,⋯,xd)；然后第二步：将点x归一化x̃ =x/‖x‖。用这种方法产生点必定均匀分布在高维球体表面。
2. Random Projection在k-means中的应用
对于k-means来说，将样本划分为距离最近的一个聚簇，这个过程可以使用下面的式子来表示：
每个数据点样本都要和聚簇中心做一次上述操作，所以一次迭代过程中计算复杂度为 ， 是 指 样本 维度。观察上面的式子， 的计算是可以预先完成的， 可以在每次迭代时预先计算好，而不必对每个样本都计算一次。所以更新的关键操作就是 的计算，即计算数据样本矩阵 和 聚簇 中心 的内积 。所以我们可以想办法在样本矩阵上做操作来减小计算的复杂度。
准备数据
首先，我们将为本教程生成简单的随机数据。在这里，我们使用具有1000个特征的数据集。
为了将维度方法应用于真实数据集，我们还使用Keras API的MNIST手写数字数据库。MNIST是三维数据集，这里我们将把它重塑为二维的。
print(x.shape)
mnist.load_data()
print(x_train.shape)
reshape(x_train,)
print(x_mnist.shape)
高斯随机投影
高斯随机法将原始输入空间投射到一个随机生成的矩阵上降低维度。我们通过设置分量数字来定义该模型。在这里，我们将把特征数据从1000缩减到200。
grp.fit_transform(x)
print(gshape)
根据你的分析和目标数据，你可以设置你的目标成分。
稀疏随机投影
稀疏随机方法使用稀疏随机矩阵投影原始输入空间以减少维度。我们定义模型，设置成分的数量。在这里，我们将把特征数据从1000缩减到200。
srp_data = srp.fit_transform(x)
print(srp_data.shape)
根据你的分析和目标数据，你可以设置你的目标成分。
PCA投影
我们将使用PCA分解，通过设置成分数来定义模型。在这里，我们将把特征数据从1000缩减到200。
pca.fit_transform(x)
print(pca_data.shape)
根据你的分析和目标数据，你可以设置你的目标成分。
MNIST数据的投影
在使用高斯、稀疏随机和PCA方法学习降维后，现在我们可以将这些方法应用于MNIST数据集。为测试目的，我们将设置2个成分并应用投影。
#对2个成分的稀疏随机投影
srp.fit_transform(x_mnist)
df_srp["comp1"] = z[:,0)
df_srp["comp2"] = z[:,1] 。
# 高斯随机投射在2个成分上
fit_transform(x_mnist)
# 对2个成分进行PCA
PCA(n=2)
随时关注您喜欢的主题
我们将通过可视化的方式在图中检查关于预测的结果。
sns.scatterplot(x="comp-1", y="comp-2")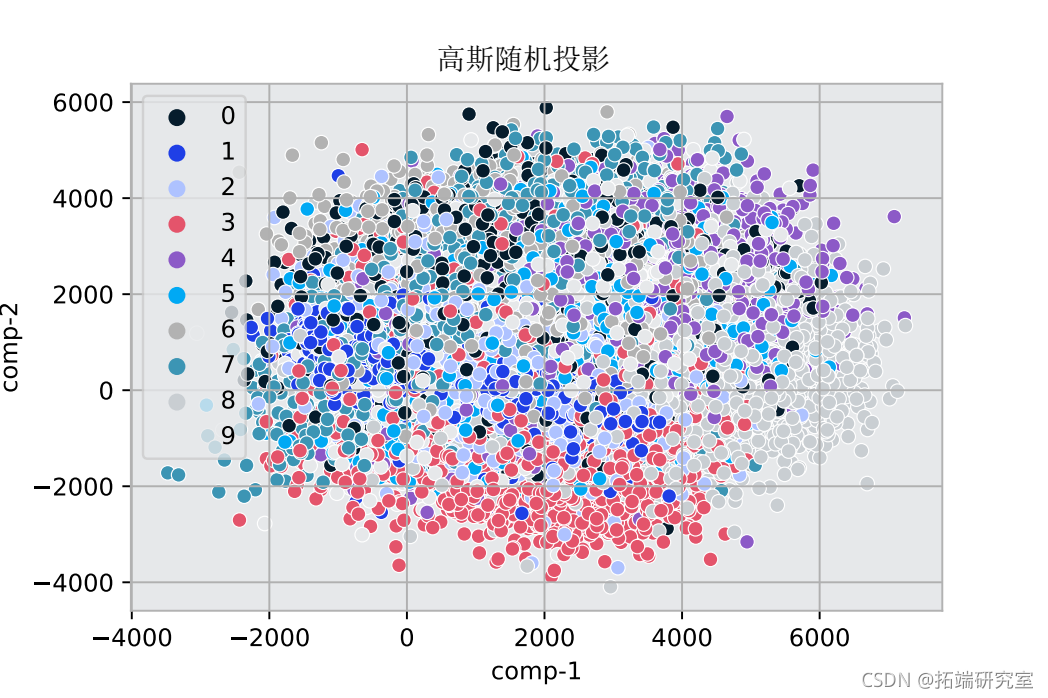
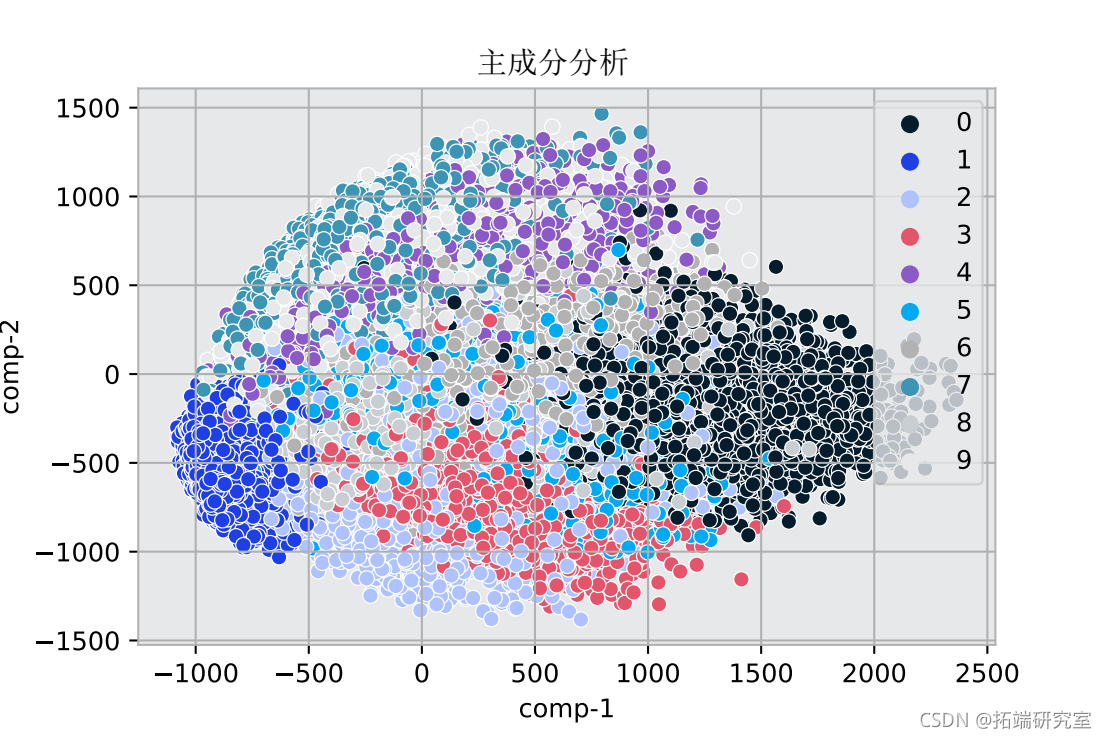
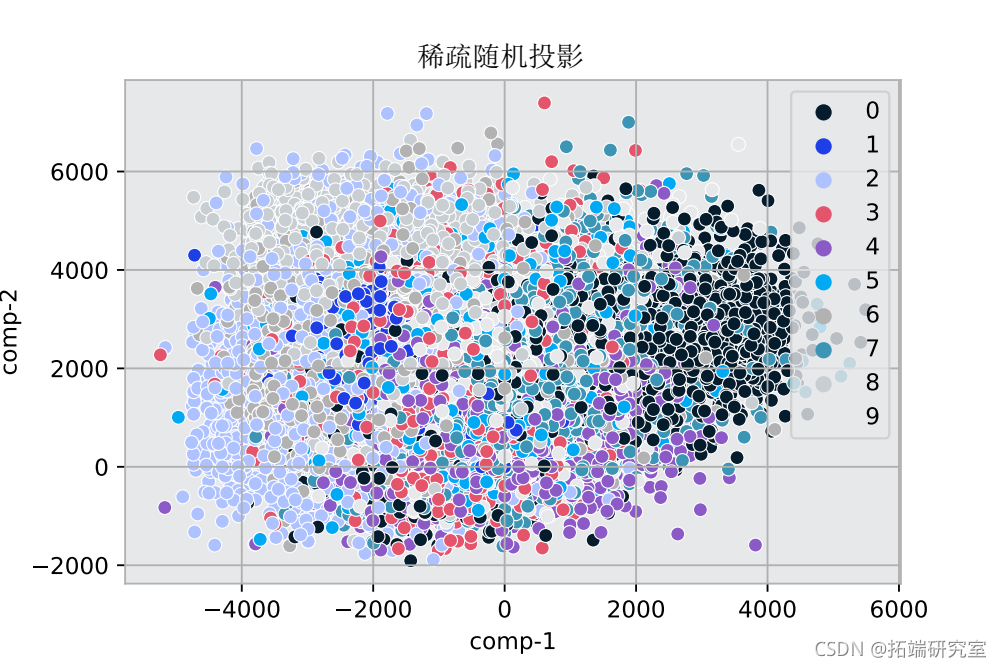
该图显示了MNIST数据的变化维度。颜色定义了目标数字和它们的特征数据在图中的位置。
在本教程中，我们已经简单了解了如何用稀疏和高斯随机投影方法以及Python中的PCA方法来减少数据维度。
R语言聚类分析、因子分析、主成分分析PCA农村农业相关经济指标数据可视化
R语言逻辑回归、GAM、LDA、KNN、PCA主成分分析分类预测房价及交叉验证
R语言主成分PCA、决策树、boost预警模型数据挖掘在跨区域犯罪研究分析
R语言大学城咖啡店消费问卷调查报告：信度分析、主成分分析PCA可视化
